Сколькими способами можна распределить 12 классных комнат под 12 учебных кабинетов? С подробным описанием.
Задача о покрытии конечного множества системой его подмножеств (12 из 12)
Пусть имеем некоторое множество и систему его подмножеств. Требуется найти минимальное количество подмножеств, покрывающих исходное множество. Задачу можно представить с помощью двудольного графа: к первой доле относятся элементы первого множества, ко второму — подмножества (одно подмножество — одна вершина) . Вершины первой и второй долей соединяются ребром, если множество вершины второй доли содержит элемент вершины первого множества. Требуется удалить как можно больше вершин из второй доли с инцидентными ей ребрами, но чтобы каждой вершине первой доли осталось хотя бы одно инцидентное ребро.
Пусть, например, исходное множество содержит 12 элементов <1,2. 12>, а система подмножеств следующая: <2, 3>, <4, 8, 10>, <1, 6>, <6, 9>, <2, 11>, <5, 7>, <4, 5, 12>, <8, 11>, <3, 9>, <11>. Тогда в алгебраической форме (на NP-языке) эта задача выглядит следующим образом
Project Cover2
Module Main2
Var x1 As Boolean
Var x2 As Boolean
Var x3 As Boolean
Var x4 As Boolean
Var x5 As Boolean
Var x6 As Boolean
Var x7 As Boolean
Var x8 As Boolean
Var x9 As Boolean
Var x10 As Boolean
Var x11 As Boolean
Var x12 As Boolean
Con c1 As x2+x3>=1
Con c2 As x4+x8+x10>=1
Con c3 As x1+x6>=1
Con c4 As x6+x9>=1
Con c5 As x2+x11>=1
Con c6 As x5+x7>=1
Con c7 As x4+x5+x12>=1
Con c8 As x8+x11>=1
Con c9 As x3+x9>=1
Con c10 As x11>=1
Con e1 As
Minimize(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12)
Источник
Задания для самостоятельной работы
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Основные формулы комбинаторики
1. Элементы комбинаторики.
Элементы комбинаторики
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три основных вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.
Размещения
Размещениямииз п элементов по т в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
Число размещений из n элементов по т обозначается символом 

Найти число размещений:
1) по 10 элементов по 4;
1) 
2) 
Решить уравнение 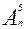

 |  |  |
ОДЗ: n 


n – 2 


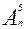

Вычислить значения выражений:
2) 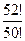
1) 5! + 6! = 5∙4∙3∙2∙1 + 6∙5∙4∙3∙2∙1 = 120 + 720 = 840;
2) 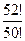

Перестановки
Перестановкамииз п элементов называются такие соединения из всех п элементов, которые отличаются друг от друга порядком расположения элементов.
Число перестановок из п элементов обозначается символом Рп. Перестановки представляют частный случай размещений из п элементов по п в каждом, т. е.
Рп = 
Число всех перестановок из и элементов равно произведению последовательных чисел от 1 до п включительно. Произведение 1•2•3 . (п—1)п обозначают символом п! (читается «п-факториал»), причем полагают 0! = 1, 1! = 1. Поэтому равенство (2) можно переписать в виде
Используя формулу (3), формуле (1) можно придать вид



При решении задач часто используется равенство
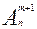

Составить всевозможные перестановки из элементов:
Сочетания
Сочетаниями из п элементов по т в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из п элементов по т обозначается 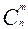
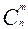

которую можно записать также в виде
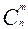

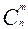

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
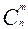
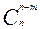


(по определению полагают 

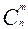

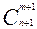
1) 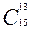
2) 

1) 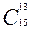

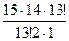
2) 



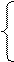

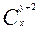

ОДЗ: х 


Подставим х = 12 в первое уравнение системы, получим





Задания для самостоятельной работы
Задача1. Найдите число размещений: 1) 

Задача 2. Вычислите:
1) 
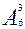
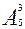


Задача 3. 30 учащихся обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?
Задача 4. Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
Задача 5. Решите уравнения:
1) 






6) 


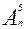


Задача 6. Cоставьте всевозможные перестановки из букв: a, b, c, d.
Задача 7. Вычислите значения следующих выражений:
1) 
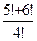
Задача 8. Докажите тождества:
1) 
2) 
Задача 9. Сократите дроби:
1) 


Задача 10. Выполните действия:
1) 



3) 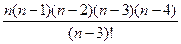
Задача 11. Сколькими способами можно составить список из 10 человек?
Задача 12. Сколькими способами можно распределить 12 классных комнат под 12 учебных кабинетов?
Задача 13. Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторений?
Задача 14. Сколькими способами можно рассадить 7 человек по 7 местам?
Задача 15. Вычислите:
1) 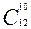



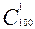
Задача 16. Проверьте равенства:
1) 
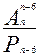
2) 

3) 


4) 

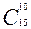
5) 

6) 
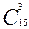

Источник





