Сколькими способами можно раскрасить квадрат

Спрашивали? Отвечаем!

Насколько я понимаю, Вас интересует не столько задача, сколько её решение. Сама задача уже широко растиражирована в сети. Например, полная постановка есть на яндексе. Кратко пример решения я покажу ниже, но призываю помнить о том, что это задача не на листы, а на подобие геометрических фигур. Подобными бывают не только треугольники! Но любые фигуры одинаковой формы с пропорциональными размерами. В следующий раз это может оказаться задачей на болты и гайки (шестиугольники), дуги окружностей или сектора кругов. Сконцентрируйтесь не на содержании задания, а на принципах составления пропорций для элементов подобных фигур.

Задача.
. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4?
Размер шрифта округляется до целого.

В подводке к вопросу в условии задачи подробно описаны общепринятые форматы листов бумаги. Важно, что каждый лист следующего по номеру формата получается разрезанием предыдущего на две равные части. И еще более важно, что размеры сторон самого большого листа (А0) подобраны так, что листы всех форматов подобны.

Итак, если прямоугольник ABCD – это лист формата A3, то лист формата А4 это прямоугольник A₂B₂N₂M₂. Чтобы текст, напечатанный на большем листе выглядел так же, как на меньшем, он должен увеличиться пропорционально стороне АС листа. Составим пропорцию \[\frac<АС> = \frac\] и преобразуем её с учётом \(AB = A_2B_2, \; B_2N_2 = \dfrac<2>\). \[\frac<АС> = \frac<2a_2b_2>\] Произведение крайних членов пропорции равно произведению её средних членов (или перемножаем «креcт накрест», если пропорция написана дробью). Отсюда \[ AC^2 = 2A_2B_2^2; \; AC = \sqrt2 A_2B_2.\] Таким образом, сторона листа формата А3 будет больше соответствующей стороны лиcта формата А4 в \(\sqrt2\) раз, что составляет примерно 1,41. Поэтому и шрифт должен быть увеличен в 1,41 раза, т.е. 15×1,41 = 21,15 ≈ 21 (pt).

Если же Вы планировали решать задачу через условную вероятность, то р01=k:m, p02=k:n, p03=n:m не те вероятности, которые даны в условии задачи, а некоторые другие, условные, т.к. отнесены не ко всем выпущенным чайникам, а только к тем, которые остаются исправными в течение определенного периода времени.
k:m — вероятность того, что чайник доживёт до конца испытания при условии, что он не сломался в первый год;
k:n — вероятность того, что чайник доживёт до конца испытания при условии, что он не сломался за два года (не то же самое, что за второй);
n:m — вероятность того, что чайник останется исправным к началу третьего работы при условии, что он не сломался в первый год.
Для того, чтобы оперировать с этими вероятностями Вам нужно определить k, n, m через заданные в условии задачи вероятности p1 и p2, т.е. всё равно вернуться к предположению о размере исходной партии чайников. Но в таком случае, зачем усложнять решение, используя условные вероятности?

Другие ошибки, которые встречались мне при решении этой задачи можно посмотреть на странице Типичные ошибки при решении задач по теории вероятностей.

Источник

Сколькими способами можно раскрасить квадрат

Школьник

Группа: Продвинутые
Сообщений: 10
Регистрация: 9.5.2013
Город: Кингстон

Вопрос такого плана. Есть задача из учебника Виленкина по комбинаторике (издание 2006 года): Квадрат разделен на 16 равных квадратов. Сколькими способами можно раскрасить их в белый, черный, красный и синий цвета, так, чтобы в каждом горизонтальном и каждом вертикальном ряду были все 4 цвета? Там же есть и решение, ответ — 576 способов.

Я решал таким способом:

В первом столбце возможны 4! = 24 комбинации

Б Б Б Б Б Б Ч Ч Ч Ч Ч Ч К К К К К К С С С С С С
Ч Ч С С К К Б Б К К С С Ч Ч Б Б С С Ч Ч К К Б Б
К С Ч К Ч С К С Б С К Б Б С Ч С Б Ч К Б Ч Б Ч К
С К К Ч С Ч С К С Б Б К С Б С Ч Ч Б Б К Б Ч К Ч

Допустим, выберем первую комбинацию: Б Ч К С. Тогда, в следующем столбце не может быть комбинации с Б на первой позиции, Ч на второй, К на третьей и С на четвертой. Вычеркивая данные комбинации, получим 9 возможных комбинаций для второго столбца:

Ч Ч Ч К К К С С С
Б К С Б С С К К Б
С С Б С Б Ч Ч Б Ч
К Б К Ч Ч Б Б Ч К

Допустим, выберем первую комбинацию для второго столбца: Ч Б С К. Аналогично вычеркиваем комбинации с Ч на первой позиции, Б на второй, С на третьей и к на четвертой, получаем:

Выберем комбинацию: К С Б Ч. По аналогии вычеркнем из оставшихся две комбинации. В итоге останется одна допустимая комбинация, которую поставим в 4 столбец — С К Ч Б.

Подсчитаем количество способов: 24*9*4 = 864 способа.

Как говорил выше, у Виленкина другой ответ, да и ход решения другой. Помогите, пожалуйста, разобраться в чем я не прав.

Доцент

Группа: Преподаватели
Сообщений: 4 925
Регистрация: 26.2.2007
Город: _
Вы: другое

Школьник

Группа: Продвинутые
Сообщений: 10
Регистрация: 9.5.2013
Город: Кингстон

Источник

2.8.2 Примеры решения задач

Задача 1. Сколькими способами можно пересадить четырех гостей А, Б, В, Г, сидящих соответственно на четырех местах 1, 2, 3, 4?

Решение.Рассмотрим два различных варианта расположения гостей А, Б, В, Г на четырех местах: АБВГ и БАГВ. При одинаковом составе элементов эти варианты различаются порядком следования букв. Это задача о числе перестановок. Переставляемые элементы не повторяются, поэтому воспользуемся формулой для числа перестановок без повторений: Р₄= 4! = 24. Таким образом, существует 24 различных способа расположения гостей А, Б, В, Г на четырех местах.

Задача 2. Сколькими способами можно выбрать три из пяти различных книг?

Решение. Рассмотрим множество номеров книг <1, 2, 3, 4, 5>. Из этого множества будем выбирать три элемента. Рассмотрим две такие выборки: <1, 2, 3>и <3, 1, 2>. Они не отличаются друг от друга. В самом деле, оба варианта указывают на то, что будут выбраны первая, вторая и третья книги. Рассматриваемая задача принадлежит классу задач о числе сочетаний, в данном случае эти сочетания из пяти по три элемента. В рассматриваемых сочетаниях недопустимы повторения, так как вариант <1, 1, 2>указывает на то, что будут выбраны две книги вместо трех, ими будут первая и вторая книги. Используем формулу для числа сочетаний без повторений, получаем, что искомое число способов равно.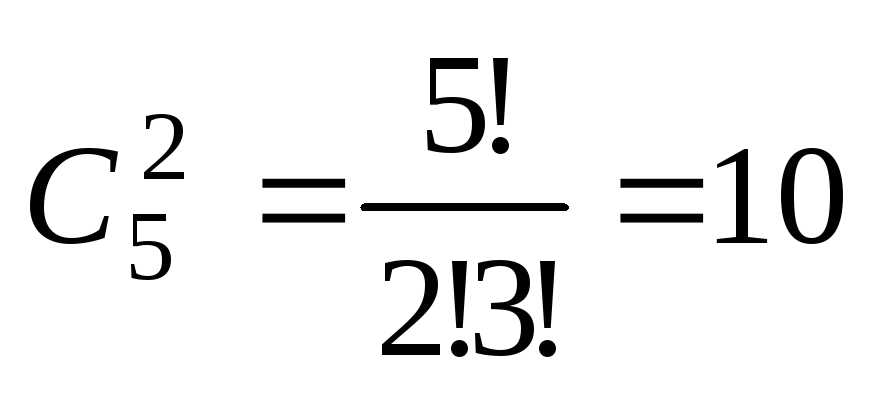

Задача 3.Сколькими способами из группы 15 человек можно выбрать старосту, культорга, профорга?

Решение. Пронумеруем должности: 1 – староста, 2 – культорг, 3 – профорг. Рассмотрим множество студентов <А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П>. Из этого множества будем выбирать три элемента. Условимся понимать выборку АБВ так: студент А займет должность №1, студент Б – должность №2, а студент В — №3. Рассмотрим две выборки: АБВ и ВБА. Очевидно, что при одинаковом составе элементов они отличаются друг от друга. В самом деле, в первом случае на должность старосты выбран студент А, а во втором случае – студент В. Имеем задачу о числе размещений из 15 элементов по три элемента. Повторение элементов в выборках недопустимы, так как выборку АВА можно истолковать так: студент А будет и старостой, и профоргом, а В – культоргом, и в этом случае студент А займет сразу две должности. Воспользуемся формулой для числа размещений без повторений, получаем, что число способов равно.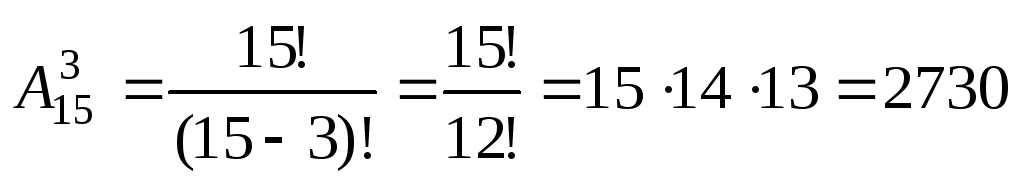

Задача 4.Сколько существует векторов с пятью координатами, принадлежащими множеству <0, 1>?

Решение. Из элементов множества <0, 1>будем выбирать пять элементов – координаты соответствующего вектора. Рассмотрим две такие выборки: (0, 1, 1, 1, 1) и (1, 1, 1, 0, 1). Они определяют различные векторы. Имеем задачу о числе размещений из двух элементов по пять элементов. Очевидно, что в рассматриваемых размещениях элементы повторяются. В данном случае используем формулу для числа размещений с повторениями, получаем, что искомое число векторов равно.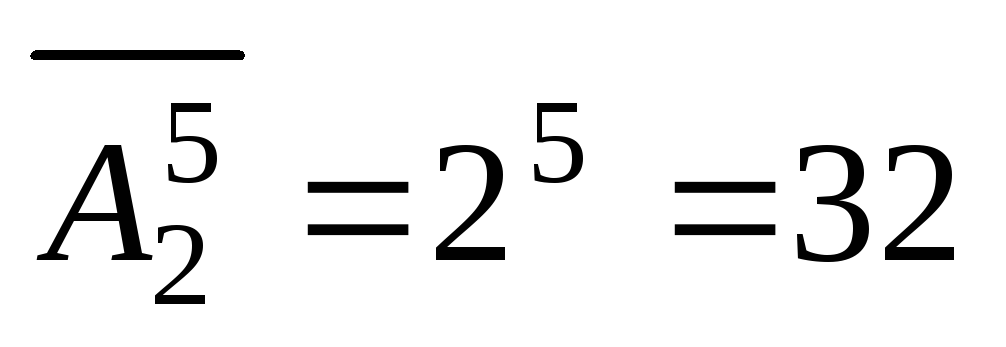

Задача 5.Сколькими способами можно раскрасить квадрат, разделенный на четыре части, пятью цветами а) допуская раскрашивание разных частей в один и тот же цвет, б) если различные части окрашиваются разными цветами?

Решение.а) Пронумеруем цвета: 1, 2, 3, 4, 5. Рассмотрим два различных варианта раскрашивания квадрата, отличающиеся друг от друга порядком следования элементов 1, 2, 3, 4:

Источник

Сколькими способами можно раскрасить квадрат, состоящий из четырёх одинаковых клеток различного цвета, если имеется 5 красок?

Математика | 5 — 9 классы

Сколькими способами можно раскрасить квадрат, состоящий из четырёх одинаковых клеток различного цвета, если имеется 5 красок?

Ответ : 20 способами.

Сколько на шахматной доске 8х8 имеется всевозможных прямоугольников, состоящих из четырёх клеток?

Сколько на шахматной доске 8х8 имеется всевозможных прямоугольников, состоящих из четырёх клеток?

Сколько клеток надо раскрасить в квадрате со стороной 10 клеток , чтобы показать 25 % ?

Сколько клеток надо раскрасить в квадрате со стороной 10 клеток , чтобы показать 25 % ?

Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины если имеется материя десяти различных цветов?

Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины если имеется материя десяти различных цветов?

Ребят если можно объясните способом комбинаторики!

Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, есле имеется материя десяти различных цветов?

Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, есле имеется материя десяти различных цветов?

Сколькими способами можно раскрасить вершины пятиугольника пятью цветами?

Сколькими способами можно раскрасить вершины пятиугольника пятью цветами.

Сриди прямоугольников состоящих из одинакового количества клеток, наименьший периметор имеет?

Сриди прямоугольников состоящих из одинакового количества клеток, наименьший периметор имеет.

Сколькими способами можно составит флаг, состоящий из трёх горизонтальных полос различных цветов, если можно использовать материал пяти различных цветов?

Сколькими способами можно составит флаг, состоящий из трёх горизонтальных полос различных цветов, если можно использовать материал пяти различных цветов?

Распишите ответ пожалуйста.

Ребят, подскажите пожалуйста?

Ребят, подскажите пожалуйста.

Сколькими способами можно раскрасить грани кубов в 6 различных цветов(различными называют цвета, которые не совмещаются при движении)Заранее спасибо : — ).

Кубик можно раскрасить так, чтобы любые соседние грани были разного цвета, а любые противоположные — одного и того же?

Кубик можно раскрасить так, чтобы любые соседние грани были разного цвета, а любые противоположные — одного и того же.

Сколько различных красок для этого потребуется?

Кубик нужно раскрасить так, чтобы любые соседние грани были разного цвета , а любые противоположные одного и того же?

Кубик нужно раскрасить так, чтобы любые соседние грани были разного цвета , а любые противоположные одного и того же.

Сколько различных красок для этогл потребуется?

На этой странице сайта, в категории Математика размещен ответ на вопрос Сколькими способами можно раскрасить квадрат, состоящий из четырёх одинаковых клеток различного цвета, если имеется 5 красок?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Источник