Сколькими способами можно представить число 1000000 как произведение 3 натуральных множителей

Комбинаторика

Задачи и теория — см. предыдущие темы по комбинаторике.

В комбинаторике ряд задач можно решить, избегая технически трудных подсчетов, удачно переформулируя условия задачи. Идея о раскладке шаров и появлении перегородок (переформулировка [10,c.135]) оказывается полезной при решении многих внешне не похожих задач. Ответ имеет вид . Рассмотрим идею переформулировки на примере следующих задач.

Задача 1. 6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?

Решение. Выложим шары в ряд. Для определения расклада наших шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая — для второго и так далее. Т. о., число вариантов раскладки шаров по ящикам равно числу способов расположения пяти перегородок. Перегородки могут стоят на любом из 19 мест (между 20 шарами -19 промежутков). Поэтому число их возможных расположений равно .

Упражнение. Сколькими способами можно разложить n одинаковых шаров по т пронумерованным ящикам так, чтобы ни один ящик не оказался пустым?

Задача 2. 6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?

Решение. Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5 одинаковых перегородок, расположенных в произвольном порядке. Каждый такой ряд однозначно соответствует некоторому способу раскладки шаров по ящикам: в первый ящик попадают шары, расположенные левее первой перегородки, во второй — расположенные между первой и второй перегородками и т. д. (между какими-то перегородками шаров может не быть). Поэтому число способов раскладки шаров по ящикам равно числу различных рядов из 20 шаров и 5 перегородок, т. е. равно ряд определяется теми пятью местами из 25, на которых стоят перегородки.

Другое решение задачи 1 можно получить так: положим сначала в каждый ящик по одному шару (теперь наверняка не будет пустых ящиков), а потом воспользуемся результатом задачи 2.

Найденные при решении двух предыдущих задач идеи позволяют изящно и легко решить следующую трудную задачу.

Задача 3. Сколькими способами натуральное число п можно представить в виде суммы

а) k натуральных слагаемых;

б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?

Указание. Представим п в виде суммы п единиц: п=1+1+…+1. Назовем теперь эти п единиц “шарами”, а k слагаемых из условия задачи — “ящиками”.Отв.: а) ; б).

Задача 4. Переплетчик должен переплести 12 одинаковых книг в красный, зеленый и синий переплеты. Сколькими способами он это может сделать?

Задача 5. Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (разрезать можно только между бусинами)?

Указание. Нужно отметить 8 мест из 30, в которых будут произведены разрезы. Отв.:

Задача 6. В кошельке лежит по 20 монет достоинством 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?

Задача 7. Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся, порядком множителей, считаются различными?

Указание. 1000000=26×56. Каждый множитель однозначно определяется количеством двоек и пятерок, входящих в его разложение. Суммарное количество в трех множителях как двоек, так и пятерок, равно 6. Ответ:

Источник

Сколькими способами можно представить число 1000000 как произведение 3 натуральных множителей

Сколькими способами можно представить 1000000 в виде произведения трёх множителей, если произведения, отличающиеся порядком множителей,
а) считаются различными?
б) считаются тождественными?

Решение

а) 10 6 = 2 6 ·5 6 . Каждый множитель однозначно определяется количеством двоек и пятёрок, входящих в его разложение. Поэтому задача сводится к разложению шести белых и шести чёрных шаров по трём различным ящикам. Аналогично задаче 30729 получаем способа.

б) Есть ровно одно разложение, не зависящее от порядка сомножителей, – в нём все множители равны 100. Те разложения, в которых есть ровно два равных множителя, мы в п. а) сосчитали трижды. В каждый из равных множителей 2 может входить в степени 0, 1, 2 или 3, то есть четырьмя различными способами; столькими же способами может входить 5. Всего получаем 16 разложений такого вида, но одно из них – рассмотренное выше разложение 100·100·100. Количество разложений с тремя различными множителями равно 784 – 1 – 3·15 = 738. Каждое из них мы сосчитали 6 раз. Всего получаем
1 + 15 + 738 : 6 = 139 разложений.

Ответ

а) способами; б) 139 способами.

Источники и прецеденты использования

олимпиада
Название	Московская математическая олимпиада
год
Номер	2
Год	1936
вариант
Тур	2
задача
Номер	4 (пункт б)
книга
Автор	Генкин С.А., Итенберг И.В., Фомин Д.В.
Год издания	1994
Название	Ленинградские математические кружки
Издательство	Киров: «АСА»
Издание	1
глава
Номер	11
Название	Комбинаторика-2
Тема	Классическая комбинаторика
задача
Номер	46 (пункт а)

Проект осуществляется при поддержке и .

Источник

Сколькими способами можно представить число 1000000 как произведение 3 натуральных множителей

Задача 31:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?

Решение:

Выложим шары в ряд. Для определения расклада наших шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая – для второго и так далее. Таким образом, число вариантов раскладки шаров по ящикам равно числу способов расположения пяти перегородок. Перегородки могут стоять на любом из 19 мест (между 20 шарами – 19 промежутков). Поэтому число их возможных расположений равно .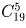

Задача 32:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?

Решение:

Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5 одинаковых перегородок, расположенных в произвольном порядке. Каждый такой ряд однозначно соответствует некоторому способу раскладки шаров по ящикам: в первый ящик попадают шары, расположенные левее первой перегородки, во второй – расположенные между первой и второй перегородками и т.д. (между какими-то перегородками шаров может и не быть). Поэтому число способов раскладки шаров по ящикам равно числу различных рядов из 20 шаров и 5 перегородок, т.е. равно 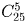(ряд определяется теми пятью местами из 25, на которых стоят перегородки).

Задача 33:

Сколькими способами натуральное число n можно представить в виде суммы

а) k натуральных слагаемых;

б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?

Решение:

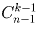
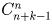
Указание. Представим n в виде суммы n единиц: n = 1 + 1 + … + 1. Назовем теперь эти n единиц «шарами», а k слагаемых из условия задачи – «ящиками». Ответ: а) ; б) .

Задача 34:

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

Решение:

.

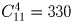
Задача 35:

Переплетчик должен переплести 12 одинаковых книг в красный, зеленый или синий переплеты. Сколькими способами он может это сделать?

Решение:

.

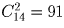
Задача 36:

Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (резать можно только между бусинами)?

Решение:

Нужно указать 8 мест из 30, в которых будут произведены разрезы. Ответ: .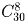

Задача 37:

30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует только за одно предложение и учитывается лишь количество голосов, поданных за каждое предложение?

Решение:

.

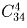
Задача 38:

В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нем

в) 8 различных открыток?

Решение:

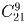
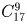
а) ; б) ; в) 10!/2! = 1814400.

Задача 39:

Поезду, в котором находится m пассажиров, предстоит сделать n остановок.

а) Сколькими способами могут выйти пассажиры на этих остановках?

б) Решите ту же задачу, если учитывается лишь количество пассажиров, вышедших на каждой остановке.

Решение:

а) n m ; б) .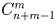

Задача 40:

В кошельке лежит по 20 монет достоинством в 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?

Решение:

.

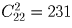
Задача 41:

Сколькими способами можно расположить в 9 лузах 7 белых и 2 черных шара? Часть луз может быть пустой, а лузы считаются различными.

Решение:

.

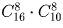
Задача 42:

Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, один апельсин, одну сливу и один мандарин?

Решение:

.

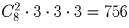
Задача 43:

Сколькими способами 4 черных шара, 4 белых шара и 4 синих шара можно разложить в 6 различных ящиков?

Решение:

.

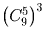
Задача 44:

Общество из n членов выбирает из своего состава одного представителя.

а) Сколькими способами может произойти открытое голосование, если каждый голосует за одного человека (быть может, и за себя)?

б) Решите ту же задачу, если голосование – тайное, т.е. учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально.

Решение:

а) n n ; б) .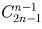

Задача 45:

Сколькими способами можно выложить в ряд 5 красных, 5 синих и 5 зеленых шаров так, чтобы никакие два синих шара не лежали рядом?

Решение:

.

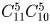
Задача 46:

Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся порядком множителей, считаются различными?

Решение:

1000000 = 2 6 • 5 6 . Каждый множитель однозначно определяется количеством двоек и пятерок, входящих в его разложение. Суммарное количество в трех множителях как двоек, так и пятерок, равно 6. Ответ: .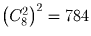

Задача 47:

На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?

Решение:

Рассмотрите 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест однозначно определяет комплект вынутых книг. Ответ: .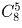

Источник

Сколькими способами можно представить число 1000000 как произведение 3 натуральных множителей

Задача 31:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?

Решение:

Выложим шары в ряд. Для определения расклада наших шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая – для второго и так далее. Таким образом, число вариантов раскладки шаров по ящикам равно числу способов расположения пяти перегородок. Перегородки могут стоять на любом из 19 мест (между 20 шарами – 19 промежутков). Поэтому число их возможных расположений равно .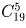

Задача 32:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?

Решение:

Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5 одинаковых перегородок, расположенных в произвольном порядке. Каждый такой ряд однозначно соответствует некоторому способу раскладки шаров по ящикам: в первый ящик попадают шары, расположенные левее первой перегородки, во второй – расположенные между первой и второй перегородками и т.д. (между какими-то перегородками шаров может и не быть). Поэтому число способов раскладки шаров по ящикам равно числу различных рядов из 20 шаров и 5 перегородок, т.е. равно 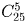(ряд определяется теми пятью местами из 25, на которых стоят перегородки).

Задача 33:

Сколькими способами натуральное число n можно представить в виде суммы

а) k натуральных слагаемых;

б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?

Решение:

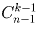
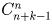
Указание. Представим n в виде суммы n единиц: n = 1 + 1 + … + 1. Назовем теперь эти n единиц «шарами», а k слагаемых из условия задачи – «ящиками». Ответ: а) ; б) .

Задача 34:

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

Решение:

.

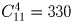
Задача 35:

Переплетчик должен переплести 12 одинаковых книг в красный, зеленый или синий переплеты. Сколькими способами он может это сделать?

Решение:

.

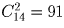
Задача 36:

Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (резать можно только между бусинами)?

Решение:

Нужно указать 8 мест из 30, в которых будут произведены разрезы. Ответ: .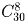

Задача 37:

30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует только за одно предложение и учитывается лишь количество голосов, поданных за каждое предложение?

Решение:

.

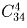
Задача 38:

В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нем

в) 8 различных открыток?

Решение:

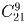
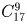
а) ; б) ; в) 10!/2! = 1814400.

Задача 39:

Поезду, в котором находится m пассажиров, предстоит сделать n остановок.

а) Сколькими способами могут выйти пассажиры на этих остановках?

б) Решите ту же задачу, если учитывается лишь количество пассажиров, вышедших на каждой остановке.

Решение:

а) n m ; б) .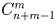

Задача 40:

В кошельке лежит по 20 монет достоинством в 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?

Решение:

.

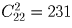
Задача 41:

Сколькими способами можно расположить в 9 лузах 7 белых и 2 черных шара? Часть луз может быть пустой, а лузы считаются различными.

Решение:

.

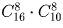
Задача 42:

Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, один апельсин, одну сливу и один мандарин?

Решение:

.

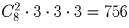
Задача 43:

Сколькими способами 4 черных шара, 4 белых шара и 4 синих шара можно разложить в 6 различных ящиков?

Решение:

.

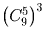
Задача 44:

Общество из n членов выбирает из своего состава одного представителя.

а) Сколькими способами может произойти открытое голосование, если каждый голосует за одного человека (быть может, и за себя)?

б) Решите ту же задачу, если голосование – тайное, т.е. учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально.

Решение:

а) n n ; б) .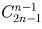

Задача 45:

Сколькими способами можно выложить в ряд 5 красных, 5 синих и 5 зеленых шаров так, чтобы никакие два синих шара не лежали рядом?

Решение:

.

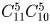
Задача 46:

Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся порядком множителей, считаются различными?

Решение:

1000000 = 2 6 • 5 6 . Каждый множитель однозначно определяется количеством двоек и пятерок, входящих в его разложение. Суммарное количество в трех множителях как двоек, так и пятерок, равно 6. Ответ: .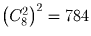

Задача 47:

На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?

Решение:

Рассмотрите 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест однозначно определяет комплект вынутых книг. Ответ: .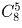

Источник