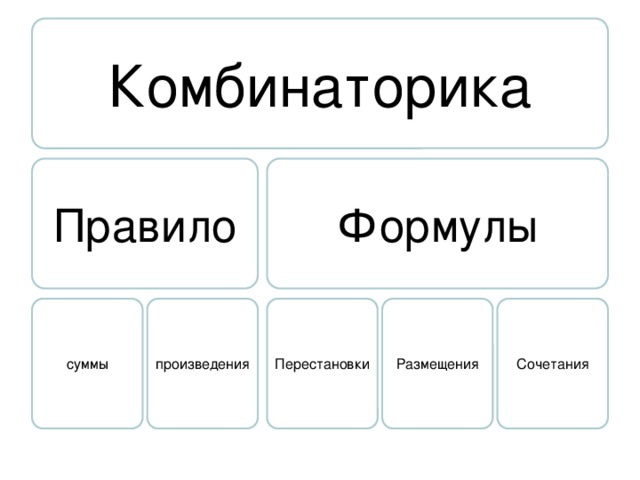
- дискретная-математика — Сколькими способами можно поселить 7 студентов в три комнаты
- Цикл задачек
- Подготовка к ЕГЭ по математике (В4). Решение комбинаторных задач.
- Содержимое разработки
- Сколькими способами можно поселить 7 студентов
- Как написать хороший ответ?
- Сколькими способами можно поселить 7 студентов
дискретная-математика — Сколькими способами можно поселить 7 студентов в три комнаты
Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
задан 7 Ноя ’19 19:10
@man123, по-моему, 105 способов. Есть 7 способов поселить одного из студентов в одноместную. Затем в двуместную селим 2 из 6 оставшихся, это 15 способов, а остальных четырёх ровно одним способом в 4-местную, и того $%7\cdot 15\cdot 1=105$%.
@man123, 2) для проверки можно в обратную сторону прокрутить. Селим 4 из 7 в 4-местную, это 35 способов, затем 2 из оставшихся трёх селим в двуместную, это ещё 3 способа, и остался один студент, его поселим в 1-местную, итого $%35\cdot 3\cdot 1=105$%, всё сошлось.
@man123, 3) можно сделать задачу интереснее, если ввести дополнительные ограничения. Например, пусть среди студентов будут как парни, так и девушки, и пусть будет запрещено селить девушек и парней в одной комнате.
А теперь вопрос авторам задачи. Вы где видели одноместные комнаты в студенческих общагах? Такого люксуса даже в Гарварде нет!
@Казвертеночка, Вы где видели одноместные комнаты в студенческих общагах? Такого люксуса даже в Гарварде нет! — фи, Гарвард отстой. у нас в универе в общагах были блоки из двух комнат — трёхместной и одноместной.
@Казвертеночка: в Главном Здании МГУ я жил и в одноместных, и в двуместных, а большие комнаты могли быть и на 4 места. Так что всё правдоподобно.
@all_exist, @falcao, спасибо, теперь буду знать. Тем не менее, моё личное мнение таково, что селить студента одного в комнате не совсем полезно, как для самого студента, так и для общества. Студент замкнётся в себе и утратит социальные навыки, станет нелюдимым, одичает. Или даже, упаси Господь, руки на себя наложит. И потом, есть люди, которые панически боятся спать одни.
@Казвертеночка: мы, будучи аспирантами, жили вдвоём в блоке, но у каждого была своя комната. А общение при этом было очень «интенсивным», то есть мы друг у друга постоянно собирались в компании. А если бы жили с соседями, то это было бы трудно, так как шумное общество кому-то может мешать. А сама традиция вполне «каноническая» — Царскосельский Лицей, «кельи», и так далее.
Источник
Цикл задачек
Приветствую. В свое время потратил немного времени на подготовку школьников к олимпиадным задачкам (5-6 классы). А недавно прочитал известную книжку «Как сдвинуть гору Фудзи?» и понял, что задачи там, в основном, похожие. А так как сегодня пятница, решил поделиться некоторыми интересными задачками.
- Известно, что 40! = 81591528324Q897734345611269596115894272000000000. Найдите цифру Q(Без вычисления 40! конечно же).
- Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
- В мешке 24 кг гвоздей. Как, имея только весы без стрелки, отмерить 9 кг гвоздей?
- Есть 101 монета, из которых 50 фальшивых, отличающихся по весу на 1 грамм от настоящих. Петя взял одну монету и за одно взвешивание на весах со стрелкой, показывающих разность на чашках в граммах, хочет определить фальшивая ли она. Сможет ли он это сделать?
- По кругу расставлено 9 чисел – 4 единицы и 5 нулей. Каждую секунду над числами проделывают следующую операцию: между соседними числами ставят ноль, если они различны, и единицу, если они равны; после этого старые числа стирают. Могут ли через некоторое время все числа стать одинаковыми?
Удачи в решении! Сегодня задачи выбрал не очень сложные. Если что, в следующую пятницу будут потруднее.
UPD: В комментариях ответы, если хотите сами подумать, то пока обгадитесь без комментарием.
Источник
Подготовка к ЕГЭ по математике (В4). Решение комбинаторных задач.
Для подготовки к ЕГЭ проведенаисистематизирована классификация различных видов комбинаторных задач с примерами решения каждого вида. Дана схема применения задач.алгоритмы решений.
Содержимое разработки
Подготовка к ЕГЭ по математике (В4) Решение комбинаторных задач
Выбираем один шар
- В коробке 10 тетрадей в клетку и 5 тетрадей в линию. Сколькими способами можно выбрать одну тетрадь?
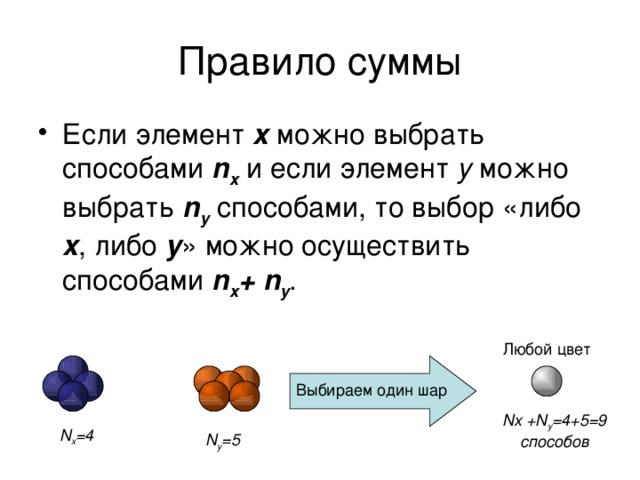
- Решение: или – логическая сумма
- 10+5=15 (выбор неважен)
- Пример1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?
- Решение:
- к1=5 –кратное 2 (2,4,16,20,28),
к2=4 – кратное 3 (3,15,21,75)
- к1+к2 = 5+4 = 9
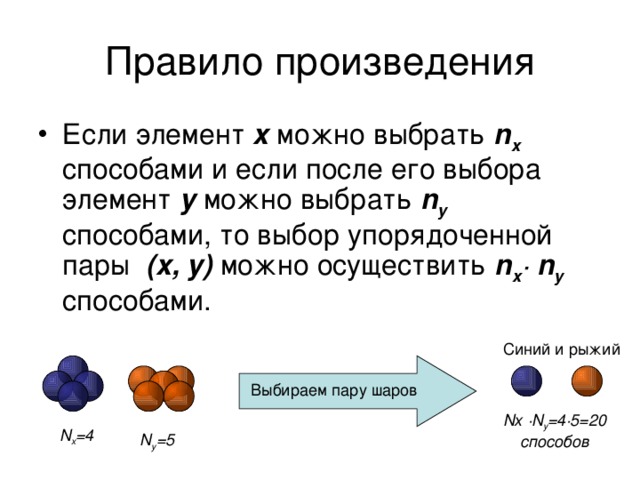
- Если элемент x можно выбрать nx способами и если после его выбора элемент y можно выбрать ny способами, то выбор упорядоченной пары (x, y) можно осуществить nx∙ ny способами.
Выбираем пару шаров
- В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
- 5*3=15
Пример 2. а) Сколько различных двузначных чисел можно составить из цифр 1,3,5,7,9?
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
- Пример5 . Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.
- а) Сколько всего стран могут использовать такую символику?
- Решение : Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N= 4х3х2х1=24
- б) Сколько стран могут использовать такую символику с синей и красной полосами, расположенными рядом?
- Решение : Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12
- Пример7 . Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы Коля и Оля оказались рядом?
- Решение : Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
- Пусть Коля сидит на краю. Место на краю можно выбрать 2 способами, после чего Олю можно посадить одним способом, после чего оставшиеся 4 места можно занять 4х3х2х1 способами, значит, всего 2х1х4х3х2х2=48 способов
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего
- По правилу сложения 48+192= 240 способов
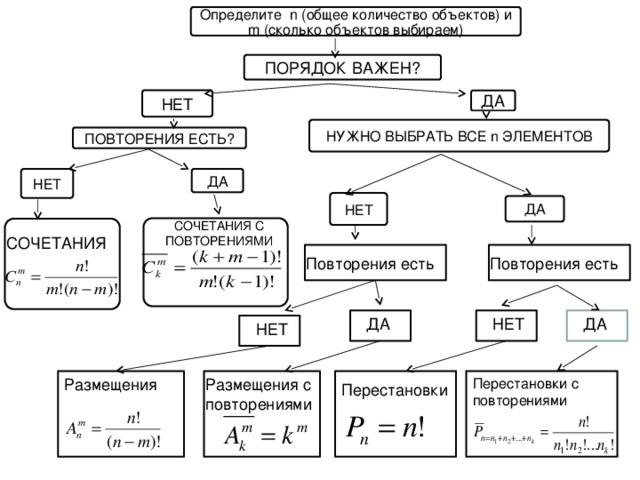
Определите n (общее количество объектов) и m (сколько объектов выбираем)
Источник
Сколькими способами можно поселить 7 студентов
Вопрос по математике:
СРОООЧНО! ЗАДАЧИ! Дам 80 баллов.
1) Сколькими способами можно поселить 7 студентов в 3 комнаты: одноместную, двухместную, 4-ёх местную?
2) Две команды разыгрывали первенство школы в 10 видах. За победу команда получала 4 очка, за ничью 2, а за поражение 1. В сумме команды набрали 46 очков. Сколько было ничьих?
Ответы и объяснения 1
2ая задача решается элементарно — 4 ничьих ибо 4*4+5*6=46 5 т.к в суме при победе одной из сторон обе команды получают 5 баллов. В 1ой вроде как 105 ибо в 4 местную можно разместить 4ех студентов 35 способами оставшуюся 3ойку в 2ух местную 3емя 3*35 = 105
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Источник
Сколькими способами можно поселить 7 студентов
Задача 1:
В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
Решение:
Выберем чашку. В комплект к ней можно выбрать любое из трех блюдец. Поэтому есть 3 разных комплекта, содержащих выбранную чашку. Поскольку чашек всего 5, то число различных комплектов равно 15 (15 = 5 3).
Задача 2:
В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца и ложки?
Решение:
Выберем любой из 15 комплектов предыдущей задачи. Его можно дополнить ложкой четырьмя различными способами. Поэтому общее число возможных комплектов равно 60 (60 = 15 4 = 5 3 4).
Задача 3:
В Стране Чудес есть три города: А, Б и В. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги. Сколькими способами можно проехать от А до В?
Решение:
Задача 4:
В Стране Чудес есть четыре города: А, Б и В и Г. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из города А в город Г – две дороги, и из города Г в город В – тоже две дороги. Сколькими способами можно проехать от А до В?
Решение:
Выделим два случая: путь проходит через город Б или через город Г. В каждом из этих случаев легко сосчитать количество возможных маршрутов: в первом – 24, во втором – 6. Складывая, получаем общее количество маршрутов: 30.
Задача 5:
В магазине «Все для чая» по-прежнему продается 5 чашек, 3 блюдца и 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?
Решение:
Возможны три разных случая: первый – покупаются чашка с блюдцем, второй – чашка с ложкой, третий – блюдце и ложка. В каждом из этих случаев легко сосчитать количество возможных вариантов (в первом – 15, во втором – 20, в третьем – 12). Складывая, получаем общее число возможных вариантов: 47.
Задача 6:
Назовем натуральное число «симпатичным» , если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?
Решение:
Понятно, что однозначных «симпатичных» чисел ровно 5. К каждому однозначному «симпатичному» числу вторая нечетная цифра может быть дописана пятью различными способами. Таким образом, двузначных «симпатичных» чисел всего 5 5 = 25. Аналогично, трехзначных «симпатичных» чисел 5 5 5 = 125, и четырехзначных – 5 5 5 5 = 54 = 625.
Задача 7:
Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?
Решение:
Задача 8:
Каждую клетку квадратной таблицы 2 × 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?
Решение:
Задача 9:
Сколькими способами можно заполнить одну карточку в лотерее «Спорт-про-г-ноз»? (В этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог каждого матча – победа одной из команд либо ничья; счет роли не играет).
Решение:
Задача 10:
Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо? Указание. Сосчитайте отдельно количества одно-, двух-, трех- и четырехбуквенных слов.
Решение:
Ответ: 3 + 3² + 3³ + 3 4 = 120.
Задача 11:
В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Решение:
Капитаном может стать любой из 11 футболистов. После выбора капитана на роль его заместителя могут претендовать 10 оставшихся человек. Таким образом, всего есть 11 10 = 110 разных вариантов выборов.
Задача 12:
Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя шести различных цветов?
Решение:
Цвет для верхней полоски флага можно выбрать шестью разными способами. После этого для средней полоски флага остается пять возможных цветов, а затем для нижней полоски флага – четыре различных цвета. Таким образом, флаг можно сделать 6 5 4 = 120 способами.
Задача 13:
Сколькими способами можно поставить на шахматную доску белую и черную ладьи так, чтобы они не били друг друга?
Решение:
Белую ладью можно поставить на любую из 64 клеток. Независимо от своего расположения она бьет 15 полей (включая поле, на котором она стоит). Поэтому остается 49 полей, на которые можно поставить черную ладью. Таким образом, всего есть 64 49 = 3136 разных способов.
Задача 14:
Сколькими способами можно поставить на шахматную доску белого и черного королей так, чтобы получилась допустимая правилами игры позиция?
Решение:
Белого короля можно поставить на любое из 64 полей. Однако количество полей, которые он при этом будет бить, зависит от его расположения. Поэтому необходимо разобрать три случая:
а) если белый король стоит в углу (углов всего 4), то он бьет 4 поля (включая то, на котором стоит), и остается 60 полей, на которые можно поставить черного короля;
б) если белый король стоит на краю доски, но не в углу (таких полей – 24), то он бьет 6 полей, и для черного короля остается 58 возможных полей;
в) если же белый король стоит не на краю доски (таких полей – 36), то он бьет 9 полей, и для черного короля остается 55 возможных полей.
Таким образом, всего есть 4 60 + 24 58 + 36 55 = 3612 способов расстановки королей.
Задача 15:
Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?
Решение:
Будем рассуждать точно так же, как при решении задач предыдущего цикла. На первое место можно поставить любую из трех цифр, на второе – любую из двух оставшихся, а на третье – последнюю оставшуюся цифру. Таким образом, всего получается 3 2 1 = 3! чисел.
Задача 16:
Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 3 2 1 = 4!.
Задача 17: Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов сожно составить из слов
Решение:
а) Так как все буквы слова различны, то всего можно получить 6! слов.
б) В этом слове две буквы И, а все остальные буквы разные. Временно будем считать разными и буквы И, обозначив их через И 1 и И 2 . При этом предположении получится 5! = 120 разных слов. Однако те слова, которые получаются друг из друга только перестановкой букв И 1 и И 2 , на самом деле одинаковы. Таким образом, полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов всего 120:2 = 60.
в) Считая три буквы А этого слова различными (А 1 , А 2 , А 3 ), получим 8! разных слов. Однако слова, отличающиеся лишь перестановкой букв А, на самом деле одинаковы. Поскольку буквы А 1 , А 2 , А 3 можно переставлять 3! способами, все 8! слов разбиваются на группы по 3! одинаковых. Поэтому разных слов всего 8!/3!.
г) В этом слове три буквы С и две буквы И. Считая все буквы различными, получаем 11! слов. Отождествляя слова, отличающиеся лишь перестановкой букв И, но не С, получаем 11!/2! различных слов. Отождествляя теперь слова, отличающиеся перестановкой букв С, получаем окончательный результат 11!/(2! 3!).
д) Ответ: 10!/(3! 2! 2!).
Задача 22:
В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?
Решение:
Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 19 = 380. Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.
Задача 23:
Сколько диагоналей в выпуклом n-угольнике?
Решение:
Задача 24:
Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать, но не переворачивать. Сколько различных бус можно сделать из 13 разноцветных бусин?
Решение:
Задача 25:
Предположим теперь, что бусы можно и переворачивать. Сколько тогда различных бус можно сделать из 13 разноцветных бусин?
Решение:
Задача 26:
Сколько существует 6-значных чисел, в записи которых есть хотя бы одна четная цифра?
Решение:
Вместо того, чтобы подсчитывать количество требуемых 6-значных чисел, определим количество 6-значных чисел, не обладающих нужным свойством. Так как это в точности те числа, в записи которых встречаются только нечетные цифры, то их количество, очевидно, равно 5 6 = 15625. Всего 6-значных чисел 900000. Поэтому количество 6-значных чисел, обладающих указанным свойством, равно 900000 – 15625 = 884375.
Задача 27:
В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?
Решение:
Задача 28:
В киоске «Союзпечать» продаются 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт с маркой?
Решение:
Задача 29:
Сколькими способами можно выбрать гласную и согласную буквы из слова «КРУЖОК»?
Решение:
Задача 30:
На доске написаны 7 существительных, 5 глаголов и 2 прилагательных. Для предложения нужно выбрать по одному слову каждой из этих частей речи. Сколькими способами это можно сделать?
Решение:
Ответ: 7 5 2 = 70
Задача 31:
У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным обменом называется обмен одной марки на одну марку или одного значка на один значок. Сколькими способами коллекционеры могут осуществить честный обмен?
Решение:
Ответ: 20 20 + 10 10 = 500
Задача 32:
Сколько существует 6-значных чисел, все цифры которых имеют одинаковую четность?
Решение:
Ответ: 5 6 + 4 5 5
Задача 33:
Надо послать 6 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно использовать трех курьеров и каждое письмо можно дать любому из курьеров?
Решение:
Задача 34:
Сколькими способами из полной колоды (52 карты) можно выбрать 4 карты разных мастей и достоинств?
Решение:
Ответ: 13 12 11 10
Задача 35:
На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)?
Решение:
Ответ: 5 + 5 4 + 5 4 3 + 5 4 3 2 + 5 4 3 2 1 = 325
Задача 36:
Сколькими способами можно поставить 8 ладей на шахматную доску так, чтобы они не били друг друга?
Решение:
Задача 37:
На танцплощадке собрались N юношей и N девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце?
Решение:
Задача 38:
Чемпионат России по шахматам проводится в один круг. Сколько играется партий, если участвуют 18 шахматистов?
Решение:
Ответ: 18 17/2 = 153
Задача 39:
Сколькими способами можно поставить на шахматную доску так, чтобы они не били друг друга а) две ладьи; б) двух королей; в) двух слонов; г) двух коней; д) двух ферзей?
Решение:
Ответ: a) 64 49/2 = 1568 б) (4 60 + 24 58 + 36 55)/2 = 1806 в) (28 56 + 20 54 + 12 52 + 4 50)/2 = 1736 г) (4 61 + 8 60 + 20 59 + 16 57 + 16 55)/2 = 1848 д) (28 42 + 20 40 + 12 38 + 4 36)/2 = 1288
Задача 40:
У мамы два яблока, три груши и четыре апельсина. Каждый день в течение девяти дней подряд она дает сыну один из оставшихся фруктов. Сколькими способами это может быть сделано?
Решение:
Задача 41:
Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
Решение:
Задача 42:
Сколькими способами можно расставить на первой горизонтали шахматной доски комплект белых фигур (король, ферзь, две ладьи, два слона и два коня)?
Решение:
Задача 43:
Сколько слов можно составить из пяти букв А и не более чем из трех букв Б?
Решение:
Ответ: 1 + 6!/5!1! + 7!/5!2! + 8!/5!3! = 84
Задача 44:
Сколько существует 10-значных чисел, в которых имеется хотя бы две одинакоые цифры?
Решение: 9 10 9 – 9 9!
Задача 45:
Каких 7-значных чисел больше: тех, в записи которых есть 1, или остальных?
Решение:
8 9 6 6 – 8 9 6 , и потому чисел с единицей больше.
Задача 46:
Кубик бросают трижды. Среди всех возможных последовательностей результатов есть такие, в которых хотя бы один раз встречается шестерка. Сколько их?
Решение:
Задача 47:
Сколькими способами можно разбить 14 человек на пары?
Решение:
Ответ: 13 11 9 7 5 3 1
Задача 48:
Сколько существует 9-значных чисел, сумма цифр которых четна?
Источник