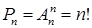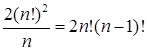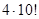Сколькими способами можно за круглым столом рассадить 5 семей?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.
Сколькими способами можно посадить за круглым столом 12 мужчин и 7 женщин?
Сколькими способами можно посадить за круглым столом 12 мужчин и 7 женщин так, чтобы никакие две.
Сколькими способами можно рассадить 6 человек за столом по кругу
Добрый день. Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по.
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин так, чтобы мужчины не.
4!*3! = 144
Стол-то круглый!
А для скамьи ответ верный 5!*3! = 720
Добавлено через 1 минуту
Кстати, у меня сомнения. Может быть 720/15 = 40 ?
Добавлено через 2 минуты
Нет, все-таки 144
Вот возьмем какую-нибудь рассадку (извиняюсь за этот термин) этих пяти семей
Неужели, пересаживая только членов той или иной семьи, мы получим лишь 6 новых рассадок? Ну и делить все же надо на 15.
Это очень коварные сестрички — Комбинаторика и Теория Вероятностей! 🙂
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.
Сколькими способами 10 мальчиков и 10 девочек можно рассадить
Сколькими способами 10 мальчиков и 10 девочек можно рассадить за 10 парт при условии, что за одной.
Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.
Сколькими способами можно рассадить в поезде 4 человек?
1. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при.
Сколькими способами группу из 30 студентов можно рассадить по 36 стульям
Прошу проверить задание. Сколькими способами группу из 30 студентов можно рассадить по 36.
Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.
Источник
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два лица одного пола не сидели рядом? 2) то же, но существенно лишь их взаимное расположение, а не конкретные занимаемые места?
Мои ответы: 1)28800 2)2, но почему то это неправильно. Возможно, я неправильно понимаю формулировку «их взаимное расположение». Кто может помочь?
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин так, чтобы мужчины не.
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.
Сколькими способами можно рассадить 6 человек за столом по кругу
Добрый день. Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по.
Сколькими способами можно составить компанию из 6 мужчин и 6 женщин?
3)У мужа 12 знакомых, среди которых 5 женщин и 7 мужчин, а у жены 7 женщин и 5 мужчин. Сколькими.
1) (С10 5 ) 2 (стулья пронумерованы)
2) Разделить на 10
Добавлено через 4 минуты
Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.
Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, уважаемые. Я к вам снова по поводу комбинаторики. Есть задача: Сколькими.
Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.
Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.
Источник
07. Перестановки
Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.
Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.
Число перестановок n различных элементов обозначают символом Pn и равно
Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?
Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем
P6P4 = 720×24 = 17280.
Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?
Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно
4! – 3! = 3×3! = 3×1×2×3 = 18.
Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?
Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем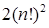 
.
Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.
Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?
5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.
Ответ: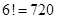 
.
5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?
Ответ: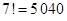 
.
5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?
Ответ: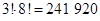 
.
5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?
Ответ: 
5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?
Ответ: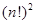 
.
5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?
Ответ: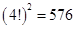 
.
5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?
Ответ: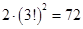 
.
5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.
Источник
Сколькими способами можно посадить 5 человек за круглый стол
В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [3].
В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.
Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементовили «круговыми перестановками».
Из истории комбинаторики
Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в Х V II в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.
Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Аг s соп j ес t ап d i” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.
Каждое расположение элементов множества в определенном порядке называют перестановкой. Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?
Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4 ۰ 3 ۰ 2 ۰ 1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1, а для множества из десяти элементов это число равно 10 ۰ 9 ۰ 8 ۰ 7 ۰ б ۰ 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1.
Вообще если множество содержит п элементов, то число перестановок равно произведению п(п – 1)(п – 2) ۰…۰ 2 ۰ 1. Множители в этом произведении можно записать в обратном порядке: 1 ۰ 2 ۰ . ۰ (п – 2)(п – 1)п.
Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).
Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:
Источник
21. Задачи
А) 
,
Б) 
,
В) 
,
Г) 
,
Д) 
,
Е) 
.
Ответ: а)
; б) 4; в) 1; г) 42; д) 4; е) 
.
А) 
,
Б) 
,
В) 
,
Г) 
,
Д) 
,
Е) 
.
Ответ: а) 
; б) 
; в) 
; г) 
; д) 
; е) 
.
3. Решить уравнения (nÎ¥):
А) 
,
Б) 
,
В) 
,
Г) 
,
Д) 
,
Е) 
.
Ответ: а) 8; б) 4; в) 10; г) 8; д) 5; е) 4.
4. Найти все n΢, удовлетворяющие условию:
А) 
,
Б) 
,
В) 
,
Г) 
,
Д) 
,
Е) 
.
Ответ: а) 
; б) 
; в) 
; г) 
; д) 
; е) 
.
5. Доказать справедливость равенств:
А) 
,
Б) 
,
В) 
,
Г) 
,
Д) 
,
Е) 
.
6. Разложить по формуле бинома Ньютона и упростить:
А) 
,
Б) 
,
В) 
,
Г) 
.
Ответ: а) 
;
Б) 
; в) 
;
Г) 
.
7. Найти средние члены разложения:
А) 
,
Б) 
.
Ответ: а) 
и 
; б) 
.
8. Решите уравнения:
А) 
б) 
в) 
Ответ: а) 4; б) 5; в) 9.
9. У одного человека есть 7 книг по математике, а у другого – 9 книг. а) Сколькими способами они могут обменять книгу одного на книгу другого? б) То же самое, но меняются две книги одного на две книги другого.
Ответ: а) 
; б) 
.
10. Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. а) Сколькими различными способами можно посадить четырех человек? б) семь человек? в) Во скольких случаях два данных человека из семи оказываются соседями? г) Во скольких случаях данный человек (из семи) имеет двух данных соседей?
Решение: а) Отношение соседства сохраняется при циклических перестановках и при симметричном отражении. В случае четырех человек мы имеем 2×4=8 преобразований, сохраняющих отношение соседства. Т. к. общее число перестановок 4 человек равно 4!=24, то имеем 24/8=3 различных способа рассадки.
Б) Если за столом сидят 7 человек, то имеем 7!/14=360 способов, вообще, а в случае n человек (n–1)!/2 способов.
В) Число способов, при которых 2 данных человека сидят рядом, вдвое больше числа способов посадить 6 человек (в силу возможности поменять этих людей местами). Значит оно равно 
.
Г) Находится аналогичным образом: 
.
11. Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? Если они садятся не за круглый стол, а за карусель и способы, переходящие друг в друга при вращении карусели, считаются совпадающими.
Ответ:
, 
.
12. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз? Во скольких случаях ровно один туз? Во скольких случаях не менее двух тузов? Ровно два туза?
Ответ:
, 
, 
, 
.
13. В купе ж/д вагона имеется два противоположных дивана по 5 мест в каждом. Из 10 пассажиров четверо желают сидеть лицом к паровозу, а трое – спиной, остальным безразлично как сидеть. Сколькими способами могут разместиться пассажиры?
Решение: Сначала выберем, кто из трех пассажиров, кому безразлично как сидеть, сядет лицом к паровозу. Этот выбор можно сделать 3 способами. На каждом диване можно пересаживать пассажиров 5! Способами. Всего получаем 
способов.
14. У мамы 2 одинаковых яблока и 3 одинаковых груши. Каждый день в течение пяти дней подряд она выдает по одному фрукту. а) Сколькими способами это можно сделать? б) Если яблок m, а груш n. в) 2 яблок,3 груши, 4 апельсина.
Ответ: а) 
; б) 
, в) 
.
15. У отца есть 5 различных апельсинов, которые он выдает своим 8 сыновьям так, что каждый получает либо один апельсин, либо ничего. Сколькими способами можно это сделать? Решите эту задачу при условии, что число апельсинов, получаемых каждым сыном, неограниченно.
Ответ: 
; 
.
16. Из группы, состоящей из 7 мужчин и 4 женщин. Надо выбрать 6 человек так, чтобы среди них было не меньше 2 женщин. Сколькими способами можно это сделать?
Ответ: 
.
17. Найти сумму всех трёхзначных чисел, которые можно написать с помощью цифр 1, 2, 3, 4. А если никакая цифра не должна появляться дважды в записи каждого числа?
Решение: Всего таких чисел 
, в них 
цифр, каждая из 4 цифр употребляется 
раза – в каждом из трёх разрядов 
раз, поэтому сумма цифр первого разряда даст 16 (1+2+3+4)=160, второго –1600 и третьего –16000. Сумма равна 17760.
Если цифры не повторяются, то таких чисел 
, в них 72 цифры, каждая из 4 цифр употребляется в каждом из 3 разрядов 6 раз, поэтому сумма 6(1+2+3+4)(1+10+100)=6660.
18. Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1,2, 3, 4, 5, если каждая цифра может встречаться в записи числа несколько раз? А если каждая цифра встречается лишь один раз?
Решение: Число должно оканчиваться: 12, 24, 32, 44, 52; первые же две цифры могут быть произвольными. Всего получаем 
чисел. Во втором случае число должно оканчиваться на одну из четырёх комбинаций: 12, 32, 52, 24; первые же две цифры могут быть выбраны из оставшихся трёх 
способами. Всего получаем 24 числа.
19. Компания из 7 юношей и 10 девушек танцует парами. а) Если в каком-либо танце участвуют все юноши, то сколько имеется вариантов участия девушек в этом танце? Сколько имеется вариантов, если учитывать лишь то, какие девушки остались неприглашенными? б) Решить те же вопросы, если относительно двух девушек можно с уверенностью утверждать, что они будут приглашены на танец.
Ответ: а) 
, 
. б) 
, 
.
20. Рота состоит из 3 офицеров, 6 сержантов, 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, двух сержантов и 20 рядовых? Решить эту задачу, при условии, что в отряд должны войти командир роты и старший из сержантов.
Ответ: 
; 
.
21. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?
Ответ: 
.
22. Сколькими способами можно расставить 20 книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг?
Ответ: Добавим к 20 книгам 4 одинаковых разделительных предмета и рассмотрим все перестановки полученных объектов. Их число равно 
.
23. Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?
Ответ: Точно так же как предыдущей задаче 
.
24. 30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует за одно предложение и учитывается лишь число голосов, полученных за каждое предложение?
Решение: Так как учитывается лишь число голосов, поданных за каждое предложение, то надо распределить 30 одинаковых «предметов» по 5 «ящикам». Для этого добавим 4 одинаковых разделительных предмета и рассмотрим все перестановки полученных объектов. Их число равно 
. Каждой перестановке соответствует своё распределение голосов.
25. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должны быть переплетены хотя бы одна книга?
Решение: 12 книг можно переплести в переплеты трёх цветов 
способами. Из них в 
случаях книги будут переплетены в не более чем два цвета, а в трех случаях – в один цвет. По формуле включений и исключений в 
случаях книги будут переплетены в переплеты всех цветов.
26. Сколькими способами можно выбрать 12 человек из 17, если данные двое человек из этих 17 не могут быть выбраны вместе?
Ответ: 
.
27. Хор состоит из 10 участников. Сколькими способами можно в течение трех дней выбирать по 6 участников, так, чтобы каждый день были различные составы хора?
Ответ: 
.
28. Человек имеет 6 друзей и в течение 20 дней приглашает к себе 3 из них так, что компания ни разу не повторяется. Сколькими способами можно это сделать?
Ответ: Так как 
, то каждый способ выбора компании будет использован ровно один раз. Число перестановок этих способов равно 20!
29. Для премии по математической олимпиаде выбраны 3 экземпляра одной книги, 2 экземпляра другой и 1 экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек и никому не дают две книги сразу? Если никому не дают двух экземпляров одной и той же книги, но могут быть вручены две или три различные книги?
Решение: Сначала выберем призеров, а потом распределим между ними книги. В результате по принципу умножения получаем 
способов. Во втором случае сначала выберем, кто получил первую книгу, потом, кто получил вторую, и, наконец, кому достанется третья книга. Всего получаем 
способов распределения премий.
30. Сколькими способами можно выбрать из 16 лошадей шестерку для запряжки так, чтобы вошли 3 лошади из шестерки ABCA’B’C’, но ни одна из пар AA’, BB’, CC’?
Решение: Выберем по одной лошади из каждой пары AA’, BB’, CC’ (8 способов выбора), трех лошадей из остальных 10 ( способов) и выберем порядок запрягания лошадей (6! способов). Всего 
способов.
31. Сколькими способами можно переставить буквы в слове «фатеция» так, чтобы не менялся порядок гласных букв?
Решение: Выпишем сначала гласные в данном порядке. Тогда для буквы «ф» имеем 5 мест. После того как они выписаны, имеем 6 мест для буквы «ц» и, наконец, 7 мест для буквы «м». Всего 
способов.
32. Сколькими способами можно переставить буквы в слове «параллелизм» так, чтобы не менялся порядок гласных букв?
Ответ: 
(следует учесть, что буква «л» входит в слово трижды.
33. Сколькими способами можно переставить буквы слова «Юпитер» так, чтобы гласные шли в алфавитном порядке?
Ответ: 
.
34. Сколькими способами можно переставить буквы слова «пастух» так, чтобы между двумя гласными были две согласные?
Ответ: Сначала фиксируем порядок гласных (2 способа), затем поставим между этими гласными 2 согласные ( 
способов). Первую из оставшихся согласных букв можно поставить до или после обеих гласных (два способа), а для второй имеем уже три места. Всего получаем 
способа.
35. Сколькими способами можно распределить 3n предметов между тремя людьми так, чтобы каждый получил n предметов?
Ответ: Расставим предметы в некотором порядке и отдадим первому человеку первые n предметов, второму – вторые n предметов и последнему – оставшиеся предметы. Поскольку порядок элементов в группах не играет роли, получаем 
.
36. Сколькими способами можно разложить 10 книг на 5 бандеролей по 2 книги в каждой (порядок бандеролей не принимается во внимание)?
Ответ: 
.
37. Сколькими способами можно раздать 18 различных предметов 5 участникам так, чтобы четверо из них получили по 4 предмета, а пятый – два предмета. Если трое получают по 4 предмета, а двое – по 3 предмета?
Решение: Располагаем участников раздела в некотором порядке. После этого располагаем всеми способами 18 предметов по порядку и делим на 4 группы по 4 предмета и 1 группу в 2 предмета. Группу в 2 предмета отдаём одному из 5 участников раздела, а остальные группы даём остальным (первую группу – первому, вторую – второму и т. д.) Так как порядок элементов в группах не играет роли, получаем 
способов раздела. Во втором случае точно так же получаем 
способов.
38. Сколькими способами можно раздать 27 книг лицам A, B и C так, чтобы A и B вместе получили вдвое больше книг, чем C?
Решение: Сначала выберем 9 книг для C. Это можно сделать 
способами. Оставшиеся 18 книг можно разделить между A и B 218 способами. Всего имеем 
способов раздела.
39. Сколькими способами можно выбрать из чисел от 1 до 100 три числа так, чтобы их сумма делилась на 3?
Решение: Возможны следующие случаи: на 3 делятся все три слагаемых, одно слагаемое и ни одного из слагаемых. В первом случае слагаемые можно выбрать 
способами. Во втором случае одно слагаемое дает в остатке 1, а другое – 2. Так как чисел от 1 до 100, дающих в остатке 1, имеется 34, а чисел, делящихся на 3, а также дающих в остатке 2, имеется по 33, то во втором случае имеем 
способов. Если все три слагаемых не делятся на 3, то они дают либо остатки 1, 1 и 1, либо 2, 2 и 2. Соответственно получаем 
или способов. Всего имеем 
способа.
40. Сколькими способами можно выбрать из 3n последовательных целых чисел три числа так, чтобы их сумма делилась на 3?
Ответ: 
.
41. На плоскости проведены 4 прямые линии, из которых никакие две не являются параллельными и никакие 3 не проходят через одну точку. Сколько получится треугольников?
42. На плоскости задано n точек, из которых p лежат на одной прямой, а кроме них никакие 3 точки не лежат на одной прямой. Сколько существует треугольников, вершинами которых являются эти точки?
Решение: Если бы никакие три из n точек лежат на одной прямой, то было бы 
треугольников с вершинами в этих точках. Но p точек лежат на одной прямой, и поэтому 
треугольников надо отбросить. Остается 
треугольников.
43. На прямой взяты p точек, а на другой прямой – ещё q точек. Сколько существует треугольников, вершинами которых являются эти точки?
Ответ: Можно взять две вершины на одной прямой, а третью – на другой. Поэтому получаем 
треугольников.
44. Каждая сторона квадрата разбита на n частей. Сколько можно построить треугольников, вершинами которых являются точки деления?
Решение: Треугольники могут быть двух видов: либо все три вершины лежат на разных сторонах квадрата, либо две вершины лежат на одной стороне квадрата, а третья – на какой-либо другой. В первом случае надо выбрать три стороны квадрата из четырех (
), а потом на каждой из трех сторон по одной точке из n–1. Всего имеем 
способов выбора. Во втором случае надо выбрать сторону, где лежат две вершины (4 способа выбора) и две точки из n–1 ( 
способов), после чего выбрать одну из трёх оставшихся сторон (три способа) и точку на ней ( 
способов). Всего во втором случае имеем 
способов выбора. Итого получим 
способов.
45. Переплётчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?
Решение: 12 книг можно переплести в переплеты 3 цветов 312 способами. Из них в случаях книги будут переплетены в не более чем два цвета, а в 3 случаях – в один цвет. По формуле включений и исключений получаем, что случаях книги будут переплетены всех трех цветов.
46. На столе лежат 20 билетов. Какова вероятность того, что 3 наудачу взятых билета имеют номер не больше 5?
Ответ: 
.
47. В одной урне 3 белых и 5 черных шаров, в другой – 9 белых и 4 черных. Из каждой урны взяли по три шара. Какова вероятность того, что шары будут одного цвета?
Ответ: 
.
48. Восемь различных книг случайных образом расставляют на полке. Найти вероятность того, что три определенные книги окажутся рядом?
Ответ: 
.
49. Зенитная батарея, состоящая из 3 орудий, производит залп по группе, состоящей из 7 самолетам. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по одному и тому же самолетам.
Ответ: 
.
50. Для уменьшения общего количества игр 12 команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся в разных подгруппах.
Ответ: 
.
51. Для уменьшения общего количества игр 2n команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в одной подгруппе.
Ответ: а) 
, б) 
.
52. Зенитная батарея, состоящая из k орудий, производит залп по группе, состоящей из l самолетов (k£l). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, все k орудий выстрелят по одной и той же цели.
Ответ: 
.
53. Из множества чисел <1, 2, . , n>последовательно выбирается два числа. Какова вероятность, что второе число больше первого, если выбор осуществляется: а) без возвращения; б) с возвращением?
Ответ: а) 
, б) 
.
54. Из множества чисел <1, 2, . , n>последовательно выбирается три числа. Какова вероятность того, что второе число будет заключаться между первым и третьим, если выбор осуществляется: а) без возвращения; б) с возвращением?
Ответ: а) 
, б) 
.
55. На бочонках лото написаны числа от 1 до N. Из этих N бочонков одновременно случайно выбираются два. Найти вероятность того, что: а) на обоих бочонках написаны числа, меньше чем k (2 2). Найти вероятность того, что два фиксированных лица А и В окажутся рядом.
Ответ: 
.
57. N человек случайным образом рассаживаются за прямоугольным столом вдоль одной из его сторон (N>2). Найти вероятность того, что два определенных лица А и В окажутся рядом.
Ответ: 
.
58. Урна содержит шары с номерами 1, 2, . , n. Из нее k (k£n) раз вынимается шар и каждый раз возвращается обратно. Найти вероятность того, что номера вынутых шаров образуют строго возрастающую последовательность.
Ответ: 
.
Источник
