Сколькими способами можно посадить 3 немцев

15. Формула включений и исключений

Принцип сложения можно применять в тех случаях, когда все множество перечисляемых комбинаций разбивается на попарно непересекающиеся группы комбинаций. Обобщим принцип сложения на случай, когда могут иметь место случаи непустых пересечений.

Пусть имеется n предметов, которые могут обладать двумя свойствами A и B. При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или обоими свойствами. Обозначим через n(A), n(B), n(AB) количество предметов, обладающих свойством A, свойством B, обоими свойствами. Тогда число предметов, обладающих хотя бы одним из указанных свойств, равно

. (13.1)

Появление третьего слагаемого связано с тем, что число предметов обладающих обоими свойствами при сложении n(A) и n(B) учитывались дважды (см. рис. 13.1).

Формула (13.1) является частным случаем более общей формулы:

(13.2)

Которую называют формулой перекрытий, или формулой включений и исключений. Чаще эту формулу записывают в следующем виде.

Обозначим символом 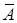свойство A, которым данные предметы не обладают. Тогда число предметов, не обладающих ни одним из указанных свойств, будет равно

(13.3)

Здесь алгебраическая сумма распространена на все комбинации свойств A1,…,Am (без учета их порядка), причем знак «+» ставится, если число учитываемых свойств четно, и знак «–», если это число нечетно. Название формулы (13.2) как формулы включений и исключений связано с тем, что сначала исключаются все предметы, обладающие хотя бы одним из свойств, потом включаются предметы, обладающие по крайней мере двумя из этих свойств, после этого исключаются предметы, обладающие по крайней мере тремя свойствами, и т. д.

В случае трёх свойств формулы (13.2) и (13.3) примут вид:

, (13.4)

. (13.5)

Пример 13.1. В научно-исследовательском институте работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык и 23 – оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?

Решение. Обозначим через A – сотрудников, знающих английский язык, через B – сотрудников, знающих немецкий язык. По условию

.

Итак, 8 человек не знают ни английского, ни немецкого языка.

Пример 13.2. Сколько можно сделать перестановок из n элементов, в которых данные два элемента a и b не стоят рядом? Данные три элемента a, b, c не стоят рядом (в любом порядке)? Никакие два из элементов a, b, c не стоят рядом?

Решение. Если a и b стоят рядом, то их можно объединить в один знак. Учитывая, что a и b можно переставлять местами, получаем перестановок, в которых a и b стоят рядом. Тогда в

Случаях они не стоят рядом. Точно также получаем, что a, b, c не стоят рядом

Случаях. Никакие два из элементов a, b, c не стоят рядом

Случаях (формула включений и исключений).

Пример 13.3. Сколькими способами можно посадить рядом 3 англичан, 3 французов и 3 немцев так, чтобы никакие три соотечественника не сидели рядом?

Решение. 9 человек можно пересаживать 9! способами. Найдём, во скольких перестановках 3 англичанина сидят рядом. Все такие перестановки получаются из одной пересаживанием между собой англичан (3! способов) и 3 французов и 3 немцев и компании из трех англичан (7! способов). Всего получаем 3!7! перестановок. Во стольких же перестановках сидят рядом 3 французов и во стольких же – 3 немцев. Далее, в (3!)25! перестановках сидят рядом трое англичан и трое французов, а также трое англичан и трое немцев, трое французов и трое немцев. И, последнее, в (3!)4 перестановках сидят рядом и англичане, и французы, и немцы. В результате, по формуле включений и исключений, находим

способа.

13.1. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек, и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?

13.2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык, 6 человек знает английский язык, 6 – немецкий, 7 – французский, 4 знают английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Сколько человек знают только один язык?

Ответ: По формуле включений и исключений число работающих равно 6+7+6–4–3–2+1=11. Только английский знают 6–4–2+1=1, только немецкий 6–4–3+1=0, только французский 7–3–2+1=3. Т. о., только один язык знают 4 человека.

13.3. Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом». Покажите, что в этих сведениях есть ошибка.

Ответ: Число школьников, которые не учатся на хорошо и отлично и не занимаются спортом, равно 45–30–28+17=4. Число мальчиков, которые не учатся на хорошо и отлично и не занимаются спортом, равно 25–16–18+15=6, т. е. их больше 4, что не может быть.

13.4. В лифт сели 8 человек. Сколькими способами они могут выйти на четырех этажах так, чтобы на каждом этаже вышел, по крайней мере, один человек?

Ответ: 8 пассажиров могут распределиться между этажами 48 способами. Из них в 38 случаях на данном этаже, 28 случаях на данных двух этажах и в 1 случае на данных трех этажах не выйдет ни один человек. По формуле включений и исключений получаем способа.

13.5. Сколько неотрицательных целых чисел, меньших чем миллион, содержит все цифры 1, 2, 3, 4? Сколько чисел состоит только из этих цифр?

Ответ: По формуле включений и исключений получаем, что все цифры 1, 2, 3, 4 содержат чисел. Только из цифр 1, 2, 3, 4 состоят чисел.

Источник

комбинаторика — Рассадка за круглым столом

Сколькими способами можно посадить за круглым столом $%3$% англичан, $%3$% французов и $%3$% немцев так, чтобы никакие три соотечественника не сидели рядом?

задан 30 Апр ’17 22:03

dolnikov
474 ● 3 ● 24
95&#037 принятых

1 ответ

Будем считать, что все места за столом пронумерованы, и что все люди — разные (другие варианты трактовки можно свести к рассматриваемому).

Общее число способов рассадить 9 человек равно $%9!$%. Далее применяем формулу включений и исключений. Пусть все англичане сидят рядом. Загадываем 9 способами место для среднего из них, затем $%3!$% способами принцип их рассадки по трём местам, и далее остаётся $%6!$% способов для рассадки остальных. Получается $%9\cdot3!\cdot6!$% способов, и столько же способов будет, если рядом сидят трое французов, а также трое немцев.

Пусть теперь рядом сидят три англичанина и три француза. Для рассадки англичан имеем, как и выше, $%9\cdot3!$% способов. Осталось 6 мест, и из них можно 4 способами выделить три места подряд для французов. Домножаем на $%3!$%, а затем ещё раз на $%3!$% для рассадки немцев. Итого будет $%9\cdot3!\cdot4\cdot3!^2$%. Столько же способов получается для двух симметричных вариантов (подряд сидят англичане и немцы, или же французы и немцы).

Наконец, пусть все три группы сидят подряд. Для англичан выбираем рассадку $%9\cdot3!$% способами, затем $%2\cdot3!$% для французов, и $%3!$% для немцев. Все эти числа перемножаем.

Теперь формула включений и исключений даёт $%9!-3\cdot9\cdot3!\cdot6!+3\cdot9\cdot3!\cdot4\cdot3!^2-9\cdot3!\cdot2\cdot3!^2=265680$%.

Можно было работать с меньшими числами, временно считая представителей одной национальности «одинаковыми», и в конце домножая на $%3!^3$%.

Источник

Поиск количества способов рассадить людей разных национальностей

Количество способов рассадить 10 человек
Скільки є способів розсадити 10 людей по 3 вагонах так,щоб в першому були -2,в другому-3,а в.

Есть 10 людей ,где 1 жених ,1 невеста ,нужно рассадить 6 людей в ряд так , чтобы среди них были жених и невеста
сколько комбинаций ? я думал что ответ 1*1*7*6*5*4, но говорят ответ другой .

Определить R- число способов, которыми можно рассадить N учащихся за M столами
Определить R- число способов, которыми можно рассадить N учащихся за M столами при N (меньше либо.

Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин
Сколько существует способов рассадить за круглым столом 5 мужчин и 5 женщин так, чтобы мужчины не.

Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.

Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.

Комбинаторная задача. Способы рассадить людей за столом.
Сколькими способами можно посадить n мужчин n женщин за круглы стол так, чтобы никакие два лица.

Оптимизация (поиск количества всех способов разложения числа на нечетные слагаемые)
Приветствую. Задание звучит следующим образом. Задано целое положительное число n. Требуется.

Источник

Сколькими способами можно посадить 3 русских, 3 немцев, 3 французов и 3 англичан

Помогите подалуйтса, очень нужна помощь!

Сколькими способами можно посадить 3 русских, 3 немцев, 3 французов и 3 англичан так, чтобы никакие три соотечественника не сидели рядом?

Сколькими способами можно посадить в вагон 8 пассажиров?
В железнодорожном вагоне 10 мест расположены лицом по ходу поезда и 10 мест против хода поезда.

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, уважаемые. Я к вам снова по поводу комбинаторики. Есть задача: Сколькими.

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.

сколькими способами можно поставить
Энциклопедия состоит из девяти томов — с первого по девятый.Сколькими способами её можно поставить.

Всего рассадок 12!
Нужно из них вычесть те, где соотечественники сидят рядом. Это будет 4*11!
Ответ 8*11!
Но тут я мог и ошибиться. Подозрительно как-то.

Добавлено через 10 минут
Наверное, сначала их надо рассматривать как разноцветные бусинки. Потом, придавая им индивидуальность, умножить на 6 4 .

Добавлено через 9 часов 29 минут
Конечно, мое первоначальное решение совершенно неверно. При подсчете вариантов сидящих рядом соплеменников я считаю одну и ту же комбинацию несколько раз. Приходит в голову воспользоваться методом «включений-исключений», но он дает громоздкие ответы. Скорее всего, есть более рациональный подход, но чего-то пока в голову не приходит.
А по поводу бусинок — в этом может быть толк. Но пока, простите, я решения не нахожу.

Всего способов рассадить 12 чел. (без учета условий задачи) -12!
Подсчитаем, сколькими способами можно нарушить условие. Это значит, в шеренге хотя бы одна нац. стоит вместе.
1. С начала Выберем одну из нац. Это можно сделать С₄ 1 =4-мя способами.
1.1. Выбранных можно расставить 3! способами.
1.2. Теперь свяжем их одной веревкой, чтобы случайно не разбрелись, и будем считать группу как один чел-к. Стало быть у нас осталось на свободе 10 чел.
1.3. Их можно расставить 10! способами.
По принципу умножения общее число способов таких нарушений = 4*3!*10!

2. Второй тип нарушений — выбираем 2 группы Это можно сделать С₄ 2 =6 способами
2.1. Выбранные группы можно связать 2*3! способами
2.2. Осталось на свободе 8 чел (2 связанные группы считаем как 2 лица)
2.3. Из можно расставить 8! способами.
Итого нарушений 2-го типа 6*2*3!*8!

3. Нарушений 3- го типа — 4*3*3!*6! (считаем аналогично)

4. Нарушений 4 — типа — (все 4 группы связаны) — 1*4*3!*4!

Из общего число расстановок убираем число нарушений

N = 12!-4*1*3!*10! — 6*2*3!*8! -4*3*3!*6! — 1*4*3!*4!

Источник