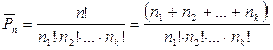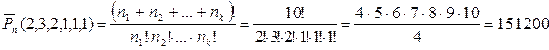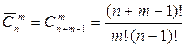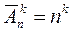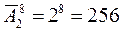Сколькими способами можно переставить буквы математика

13. Перестановки с повторениями

При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет . Мы имеем здесь дело с перестановками с повторениями.

Общую задачу сформулируем следующим образом.

Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, . Сколько можно составить различных перестановок из этих элементов?

Число перестановок c повторениями обозначают . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом способами так, что она остаётся неизменной.

Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

, (11.1) где .

Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:

.

Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?

Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем

.

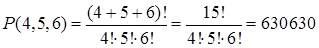
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?

Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:

.

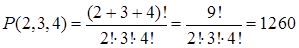
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем

.

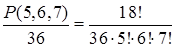
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?

Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим

.

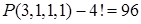
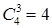
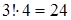
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем способа.

11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?

Ответ: .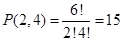

11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?

Ответ: .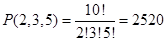

11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?

Ответ: .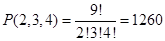

11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?

Ответ: .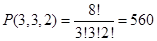

11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?

Ответ: .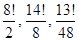

11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?

Ответ: .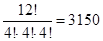

11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?

Ответ: .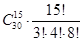

11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?

Ответ: .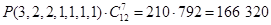

11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?

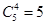
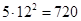
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего способов.

Источник

Сколькими способами можно переставить буквы математика

Введение в теорию множеств и комбинаторику

Практическая работа № 12. Перестановки

Вопросы к работе

1. Что такое « перестановки из n элементов»?
2. Сколько перестановок существует для n элементов?
3. Какие перестановки называются перестановками с повторениями?
4. По какой формуле вычисляется число перестановок с повторениями?

Образцы решения заданий

Пример 1.Вычислить

,

,

. Итак,

Пример 2. Сколькими способами можно рассадить на скамейке пять человек?

Решение: Способов столько, сколько различных перестановок можно составить из 5 элементов, т. е. . Итак, пять человек на скамейке можно рассадить 120 способами.

Пример 3. Сколько всех семизначных чисел, у каждого из которых цифра 6 встречается 3 раза, а цифра 5 четыре раза?

чисел.

1. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами это можно сделать? (Ответ: 2520).
2. Сколькими способами можно упаковать девять различных книг в трех бандеролях соответственно по 2, 3, 4 книги в каждой бандероли? (Ответ: ).
3. Сколькими способами можно распределить семь молодых специалистов по трем цехам, которым, соответственно, нужны 1, 2, 4 специалиста? (Ответ: ).
4. Сколькими способами можно составить список из 25 студентов? (Ответ: ).
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется одно письмо? (Ответ: ).
6. Десять лиц, которые отдельно обедают и ужинают в одной и той же столовой, просят содержателя подождать с получением денег до тех пор, пока они не пересядут за столом всеми возможными способами, если каждый день за обедом они будут сидеть по-другому. Сколько лет пришлось бы ждать содержателю столовой, если бы он согласился на это предложение? (Ответ: около 4971 года).
7. Сколькими способами 15 книг можно расположить на полке? (Ответ: 15!).
8. Сколькими способами можно переставить буквы в слове «математика»? (Ответ: ).
9. В доме отдыха давали на десерт либо яблоко, либо апельсин, либо мандарин. В течение 24 дней было выдано 9 яблок, 7 мандаринов и 8 апельсинов. Сколько различных вариантов выдачи может быть? (Ответ:
10. Сколькими способами можно переставить буквы слова «перешеек» так, чтобы 4 буквы «е» шли подряд? (Ответ: ).

Задания для самоконтроля

1. Найти все натуральные n , удовлетворяющие неравенству:

Источник

П.2 Соединения с повторениями

(2).

П.1 Соединения без повторений

Пусть дано множество М, состоящее из n элементов.

Опр. 4.1.1 Перестановки – всевозможные упорядоченные множества, составленные из всех элементов данного множества. Число всевозможных перестановок из n элементов обозначают Р_n и находят по формуле

где n!= 1×2×3× ¼ ×n, 0!=1 по определению.

Пример 4.1.1. Сколько перестановок можно составить из трех букв а, в, с?

Решение: Р₃=1×2×3=6. Действительно: авс, вас, асв, сав, вса, сва.¨

Пример 4.1.2.Сколькими способами можно переставить буквы в слове «треугольник»?

Решение: Т.к. все буквы в данном слове разные, т.е. нет повторений, то можно воспользоваться формулой (1): Р₁₁=11!=39916800.¨

Опр. 4.1.2 Размещениями изn поmназываются всевозможные упорядоченные подмножества, содержащие m элементов из данных n. Обозначаются и вычисляются по формуле:

Пример 4.1.3. Сколько можно составить четырехзначных чисел, содержащих различные цифры из 5 цифр.

Решение: Четырехзначное число – это упорядоченная последовательность цифр, т.е. имеем дело с размещениями без повторений: А₅ 4 =5×4×3×2=120. ¨

Пример 4.1.4. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами может быть составлено расписание на 1 день?

Решение: ¨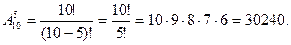

Опр. 4.1.3 Сочетаниями изn поmназываются всевозможные подмножества данных nэлементов, состоящие из m элементов. Для подсчета их числа используются следующие обозначение и формула:

(3).

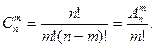
Пример 4.1.5. Сколькими способами можно из 7 различных открыток выбрать три?

Решение: Совокупность трех открыток является неупорядоченным подмножеством семи открыток, поэтому имеем дело с сочетаниями: ¨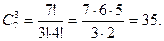

Опр: 4.2.1 Перестановками с повторениями называются перестановки из n элементов, в каждую из которых входит n₁ элементов а, n₂ элементов b, …, n_k элементов l, где n=n₁+n₂+…+n_k. Число перестановок с повторениями вычисляется по формуле:

Пример 4.2.1Сколькими способами можно переставить буквы в слове “математика”.

Решение: В слове “математика” есть повторяющиеся буквы: “м” – 2 раза, “а” – 3 раза, “т” – 2 раза, “е” – 1 раз, “и” – 1 раз, “к” – 1 раз. Порядок расположения элементов имеет значение (это очевидно, так как если переставить местами 2 буквы, то получатся разные слова) и все элементы используются, следовательно, это перестановка с повторениями.

Таким образом, в слове “математика” можно переставить буквы 151200 способами.

Опр 4.2.2 Сочетания из n элементов, в каждое из которых входит m элементов, причем один и тот же элемент может повторяться в каждом сочетании любое число раз, но не более m, называются сочетаниями с повторениями. Число сочетаний с повторениями вычисляется по формуле:

Пример 4.2.2 на почте продаются открытки 10 сортов. Сколько вариантов существует для покупки 12 открыток.

Решение: Порядок расположения элементов не имеет значения, следовательно, это сочетание. А так как открытки в наборе могут повторяться, то это сочетание с повторениями.

.

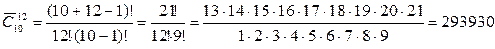
Таким образом, из 10 открыток можно выбрать набор из12 штук 293930 способами.

Опр 4.2.3 Размещениями с повторениями из n элементов по k элементов называются упорядоченные множества, каждое из которых содержит k необязательно различных элементов из данного множества n элементов. Число размещений с повторениями вычисляется по формуле:

Пример 4.2.3 В стену здания вмонтированы 8 гнезд для флажков. В каждое гнездо вставляется либо голубой, либо красный флажок. Сколько различных случаев распределения флажков на здание.

Решение: Так как порядок расположения элементов важен и не все элементы используются в данном соединении, то это размещение. А так как всего 8 гнезд, а флажков 2 вида (голубой и красный), то они будут повторяться, т.е. это размещение с повторением.

Таким образом, существует 256 способов украсить здание с 8 гнездами флажками двух цветов.

Источник