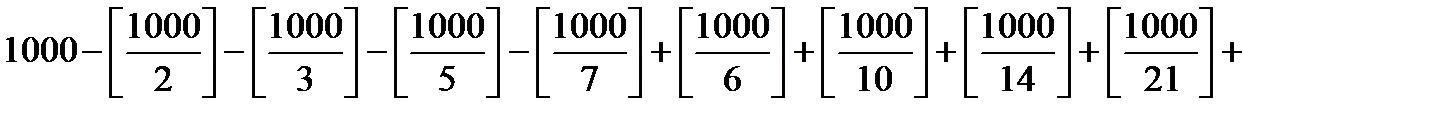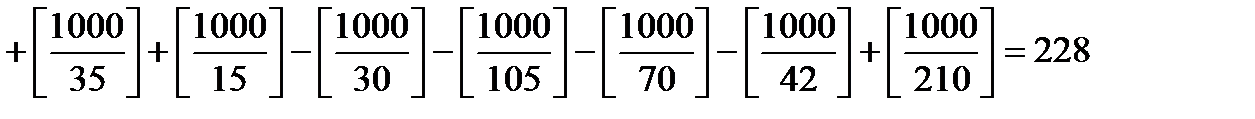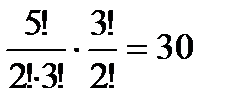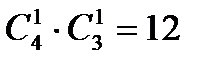13. Перестановки с повторениями
При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет 
. Мы имеем здесь дело с перестановками с повторениями.
Общую задачу сформулируем следующим образом.
Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, 
. Сколько можно составить различных перестановок из этих элементов?
Число перестановок c повторениями обозначают 
. Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом 
способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно
, (11.1) где 
.
Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:
.
Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем
.
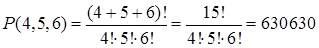
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?
Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:
.
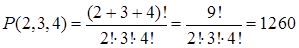
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем
.
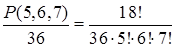
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?
Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим
.
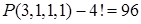
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить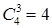 
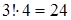
способами. Всего получаем 
способа.
11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?
Ответ: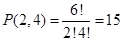 
.
11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?
Ответ: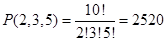 
.
11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?
Ответ: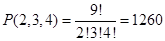 
.
11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?
Ответ: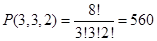 
.
11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?
Ответ: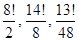 
.
11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?
Ответ: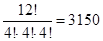 
.
11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Ответ: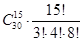 
.
11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?
Ответ: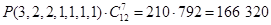 
.
11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать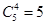 
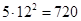
способами. Всего 
способов.
Источник
Задачи по теме «Комбинаторика»
1. Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5, если каждая цифра может встречаться в записи числа несколько раз?
Число должно оканчиваться одной из 5 комбинаций: 12, 24, 32, 44, 52. Первые же цифры могут быть произвольными. 5×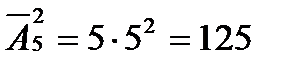 
чисел.
2. На полке находятся m+n различных книг, из которых m в черных переплетах, а n в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые m мест? Сколько положений, в которых все книги в черных переплетах стоят рядом?
Книги в черных переплетах можно переставить m! Способами, а в красных – n! способами, всего способов m!n!. Если книги в черных переплетах стоят рядом, то надо еще выбрать для них место между книгами в красных переплетах. Это можно сделать (n+1) способами. Всего имеем m!n!(n+1) способов = m!×(n!+1)!.
3.Сколько имеется девятизначных чисел, у которых все цифры различные?
0 1 2 3 4 5 6 7 8 9
4.Сколько существует целых чисел от 0 до 999, которые не делятся ни на 5, ни на 7?
Количество чисел, делящихся на 5, равно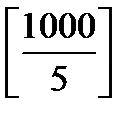 
.
Количество чисел, делящихся на 7, равно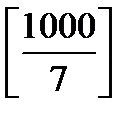 
.
Количество чисел, делящихся на 5 и на 7 —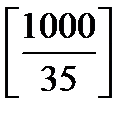 
. По формуле включений и исключений имеем:
1000- — +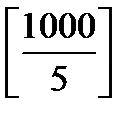 
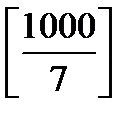
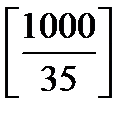
=686 чисел не делятся ни на 5, ни на 7.
5. Сколько существует целых чисел от 0 до 999, которые не делятся ни на 2, ни на 3, ни на 5, ни на 7?
6. Сколько четырехзначных чисел можно составить из цифр числа 123153?
Четырехзначное число можно составить либо из четырех различных цифр (1, 2, 3, 5), либо из двух одинаковых и двух различных (1,1,2,3; 1,1,2,5; 1,1,3,5; 1,2,3,3; 1,3,3,5; 2,3,3,5). Либо из двух пар одинаковых цифр (1,1,3,3). Поэтому общее число чисел равно: P4 + 6Р(2,1,1)+Р(2,2)=24+6×12+6=10
7. Сколькими способами можно разложить в два кармана 9 монет различного достоинства?
Каждая монета может попасть в один из этих карманов. Имеем 2 9 способов.
8. сколькими способами можно переставить буквы слова «логарифм» так, чтобы второе, четвертое и шестое места были заняты согласными?
Выберем три согласные и поставим их на заданные места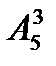 
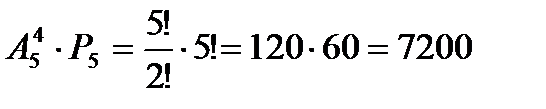
. Оставшиеся 5 букв произвольным образом расставим на остальные 5 мест (Р5=5!). Всего 
способов.
9. Сколькими способами можно выбрать из слова «логарифм» две согласных и одну гласную букву? Та же задача, если среди выбранных букв есть «ф»?
Дата добавления: 2020-11-27 ; просмотров: 137 ; Мы поможем в написании вашей работы!
Источник
Сколькими способами можно переставить буквы логарифм
Сколькими способами можно положить в ряд 2 небесно-голубых лампочки и 4 лампочки цвета травы?
Это можно сделать 
способами.
Сколькими способами можно положить в ряд 3 фисташковых лампочки и 5 лампочек цвета морской волны?
Это можно сделать 
способами.
Сколькими способами можно переставить буквы слов: а) молоток; б) мисcисипи; в) математика?
а) Перестановку можно выполнить 
способами;
б) Перестановку можно выполнить 
способами;
в) Перестановку можно выполнить 
способами.
Ответ: а) 840; б) 2 520; в) 151 200.
Сколькими способами можно переставить буквы слов: а) ротор; б) ревербератор; в) синхрофазатрон?
а) Перестановку можно выполнить 
способами;
б) Перестановку можно выполнить 
способами;
в) Перестановку можно выполнить 
способами.
Ответ: а) 30; б) 3 326 400; в) 5 448 643 200.
Источник
Комбинаторика
Комбинаторика – это раздел математики, изучающий вопросы о том, сколько различных комбинаций, подчинённых тем или иным требованиям, можно составить из элементов заданного множества.
В основе комбинаторики лежат два основных правила: правило суммы и правило произведения.
Правило суммы: если объект А можно выбрать m способами, а объект В – n способами, и при это ни один способ выбора объекта А не совпадает со способами выбора объекта В, то объект «А или В» может быть выбран (m + n) способами.
Правило произведения: если объект А можно выбрать m способами, и при каждом способе выбора объекта А, объект В может быть выбран n способами, то совместный выбор объектов А и В может быть осуществлён (mn) способами.
Комбинациями с повторениями называются комбинации, внутри которых допускается повторение элементов. Комбинации, внутри которых не могут содержаться повторяющиеся элементы, называются комбинациями без повторений.
(различаются только составом элементов)
(различаются либо составом элементов либо порядком их расположения)
(различаются только порядком расположения элементов)
k1 – число повторений I элемента,
k2 – число повторений II элемента,
kn – число повторений n-го элемента,
где m – длина комбинации, n – количество элементов множества
Замечание! Для нахождения числа сочетаний можно использовать формулу:
1) 
, 5) 
,
2) 
, 6) 
,
3) 
, 7) 
,
4) 
, 8) 
.
, или 
.
В верхней вершине треугольника и по краям каждой строки ставятся единицы, а каждое из остальных чисел будет равно сумме двух стоящих над ним слева и справа.
Основное свойство треугольника Паскаля:
Если строчки треугольника Паскаля и позиции в них нумеровать, начиная с нуля, то на k-м месте в n-й строке будет стоять значение 
.
В кружке занимаются 2 девочки и 7 мальчиков. Сколько есть способов послать на конкурс команду из 4-х человек, если в ней обязательно должна быть хоть одна девочка?
Решение. В команду входит либо одна девочка, либо обе.
В первом случае эту девочку можно выбрать способами, а также способами выбрать в команду еще трех мальчиков. По правилу произведения в этом случае × 
способов выбора.
Во втором случае в команду надо выбрать еще 2-х мальчиков разными способами. Всего по правилу суммы получаем ×+
= 91 способов выбора.
Сколько способов разложить 7 белых и 2 черных шара по 9 различным ящикам?
Решение. .Составим несколько комбинаций разложения:
(б, б, ч, б, ч, б, б, б, б), (ч, ч, б, б, б, б, б, б, б), …
Это комбинации с повторениями, одинаковые по составу, различающиеся только порядком расположения элементов – это размещения с повторениями. Тогда их число находится по формуле: 
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. В некотором государстве не найдется двух человек, у которых оказался бы одинаковый набор зубов: либо у них разное число зубов, либо зубы отсутствуют в разных местах. Какая может быть наибольшая численность населения государства, если полное число зубов у человека равно 32?
2. Сколькими способами можно распределить 12 различных учебников между четырьмя студентами? Сколькими способами можно поровну распределить 12 различных учебников между четырьмя студентами?
3. Сколькими способами можно переставлять буквы слова ЛОГАРИФМ так, чтобы второе, четвёртое и шестое места были заняты согласными буквами?
4. Из полного набора шахмат вынули 4 фигуры или пешки. Во скольких случаях среди них окажется не менее двух коней?
5. Сколькими способами можно переставить буквы слова ПЕРЕШЕЕК так, чтобы 4 буквы «Е» не стояли подряд?
6. Две команды играют в футбол до 10 голов (встреча прекращается, как только какая-то команда забьет 10 голов). В процессе игры заполняется протокол, в который вносится счет после каждого изменения счета (например, один из протоколов – 0:0, 0:1, 0:2, 1:2, . 5:10). Сколько разных протоколов может получиться?
7. Из 80 школьников 40 играют в футбол, а 50 – в волейбол. Каким может быть число школьников, играющих в обе игры; играющих хотя бы в одну из этих игр?
8. В классе 40 человек. Из них 26 человек играют в баскетбол, 25 занимаются плаванием, 27 – ходят на лыжах, при этом одновременно плаванием и баскетболом занимаются 15 человек, баскетболом и лыжами – 16, плаванием и лыжами – 18. Один человек освобождён от физкультурных занятий. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только одним видом спорта?
9. В игре «Кто хочет стать миллионером» ведущий, с целью проверить математическую грамотность участника задал ему следующий вопрос: какое число точек n нужно изобразить на плоскости так, чтобы число отрезков, соединяющих всевозможные пары различных точек, было равно 1 000 000? Участник ответил, что вопрос некорректен, т. е. такого n не существует. Как он мог это объяснить?
10. На плоскости проведено n прямых, и на каждой из них взято р точек так, что ни одна из них не является точкой пересечения прямых и никакие три не лежат на одной прямой, отличной от заданных. Найдите число треугольников с вершинами в этих точках.
11. На плоскости даны три точки А, В и С. Через точки А, В и С проведены пучки соответственно из m, n и р прямых, при этом никакие три прямые не из одного пучка не пересекаются в одной точке, и никакие две не параллельны. Найдите наибольшее возможное число треугольников, вершины которых являются точками пересечения этих прямых и не совпадают с заданными точками А, В и С.
12. Даны шесть цифр 0, 1, 2, 3, 4, 5. Найдите сумму всех четырёхзначных чётных чисел, которые можно написать этими цифрами (одна и та же цифра может повторяться).
13. Сколькими способами можно выбрать из натуральных чисел от 1 до 100 три натуральных числа так, чтобы их сумма была чётной?
14. Сколькими способами можно посадить рядом трёх англичан, трёх французов и трёх турок так, чтобы никакие три соотечественника не сидели рядом?
15. Каждая сторона квадрата разбита на n частей. Сколько можно построить треугольников с вершинами в точках деления?
16. Надо отгадать, какие пять монет держит в руке партнёр. Выбор монет такой: 1, 2, 3, 5, 10, 15, 20, 50 копеек, 1 рубль. Сколько может быть дано неверных ответов? А если все монеты в руке различного достоинства?
17. Сколько существует четырёхзначных чисел, делящихся на 4, в десятичной записи которых нет цифр 4, 5, 6, 8?
Источник
