- III. На использование формул для сочетаний
- Решение с учащимися комбинаторных задач на уроках информатики способствует значительному повышению их математической и алгоритмической культуры: развивается динамичность мышления,
- Приложение №2. Задачи
- Приложение №3. Задачи
- II. На использование формул для перестановок и размещений
- III. На использование формул для сочетаний
III. На использование формул для сочетаний
1.Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?
Для решения этой задачи необходимо использовать формулу для сочетания элементов, т.к. здесь не имеет значения порядок элементов в выборке. Запишем формулу для сочетаний и произведем вычисления:
С 
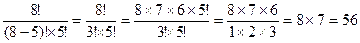
2.Компания из двадцати мужчин разделяется на три группы, в первую из которых входят три человека, во вторую — пять и в третью — двенадцать. Сколькими способами они могут это сделать? (Ответ записать в виде произведения сомножителей, не вычисляя его.)
Из 20-ти элементов необходимо сделать три выборки, причем порядок внутри выборок значения не имеет. Поэтому используем формулу для сочетаний. Чтобы выбрать из 20-ти элементов 3, существует С 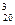
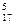
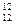
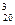

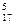

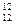
Ответ: С 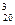

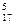

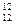
3.Сколькими способами можно отобрать несколько фруктов из семи яблок, четырех лимонов и девяти апельсинов? (Мы считаем, что фрукты одного вида неразличимы.)
Т.к. фрукты одного вида неразличимы, то существует один способ взять одно яблоко, один способ взять 2 яблока, один способ взять три яблока и т.д., т.е. всего семь способов выбрать несколько яблок (несколько – это не менее одного). Необходимо также прибавить один способ не взять ни одного яблока. Следовательно, существует 8 способов взять яблоки. Аналогично существует 5 способов выбрать лимоны и 10 способов выбрать апельсины. Следуя принципу умножения, получим все способы отбора фруктов: 7 



Источник
Решение с учащимися комбинаторных задач на уроках информатики способствует значительному повышению их математической и алгоритмической культуры: развивается динамичность мышления,
Приложение №2. Задачи
При решении этих задач следует использовать правила умножения и сложения.
1. Сколько слов можно образовать из букв слова «фрагмент», если слова должны состоять а) из восьми букв ?
Решение. а) Т.к. все буквы разные, то: 8! б)

2. Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, если первая из них не равна нулю ?
Решение. По правилу умножения, учитывая, что первая цифра не равна 0, получаем: 9*10*10*10*10
3. Сколько существует различных автомобильных номеров, если номер состоит из одной буквы, за которой следуют четыре цифры, отличные от нуля ?
Решение. Буквы «й», «ь», «ъ» не используются в автомобильных номерах, поэтому всего букв 30. Тогда по правилу умножения количество номеров: 30*9*9*9*9=1 771 470
4. Сколько существует различных автомобильных номеров, если номер состоит из одной русской буквы, за которой следует три цифры, а за ними еще две буквы ? Учесть, что первая цифра не должна быть «0», а буквы «й», «ь», «ъ» не используются ?
Решение. По правилу умножения: 30*9*10*10*30*30=24 300 000
5. Сколькими способами можно расставить на полке семь книг, если две определенные книги должны всегда стоять рядом?
Решение. Две книги, которые должны стоять рядом, будем считать одной книгой. Тогда
количество способов=6!
6. Сколькими способами можно расставить на полке семь книг, если две определенные книги не должны стоять рядом?
Решение. Так как всего возможностей 7!, то 7!-6!=6!(7-1)=6*6!
7. Три дороги соединяют города А и В, четыре дороги соединяют В и С. Сколькими способами можно совершить поездку из А в С через В и вернуться в А тоже через В?
Решение. По правилу умножения: (3*4)*(4*3)
8. Сколько различных трехбуквенных слов можно образовать, используя буквы, составляющие Вашу фамилию?
9. Сколько различных трехбуквенных слов можно образовать, используя буквы, составляющие Вашу фамилию, причем эти слова должны начинаться согласной буквой?
10. Сколько различных трехбуквенных слов можно образовать, используя буквы, составляющие Вашу фамилию, причем эти слова должны начинаться и оканчиваться согласными, а в середине должна быть гласная буква?
11. У нас есть три письма, каждое из которых можно послать по шести различным адресам. а) Сколькими способами можно осуществить рассылку писем, если никакие два письма нельзя посылать по одному адресу?
б) Сколькими способами можно разослать письма, если по одному адресу можно послать более одного письма?
Решение. а) Первое письмо можно отправить по любому адресу, т.о. возможностей всего шесть. Второе – по любому из пяти оставшихся, а третье по одному из оставшихся четырех. Всего, по правилу умножения, рассылку можно сделать 6*5*4 способами.
б) Рассуждая так же, получим: 6*6*6 способов.
Приложение №3. Задачи
1. Сколькими способами их восьми человек можно отобрать комиссию, состоящую из пяти членов?
Решение. Так как в комиссии порядок её членов не играет роли, то способов — 
2. Работодателю нужны пять сотрудников, а к нему с предложением своих услуг обратились десять человек. Сколькими способами он может выбрать среди них пятерых?
Решение. При отборе сотрудников порядок не играет роли, поэтому количество способов отбора — 
3. Сколькими способами можно отобрать несколько фруктов из семи яблок, четырех груш и девяти бананов?
Решение. Яблоки мы можем отобрать так: либо одно, либо два, либо три, либо четыре, либо пять, либо шесть, либо семь, либо ни одного: возможностей всего восемь. Рассуждая так же, для груш возможностей выбора – 5, для бананов – 10. По правилу умножения имеем: 8*5*10-1=399. Вычли 1, т.к. выбор, при котором не отобрано ни одного фрукта, надо исключить.
4. Сколько «слов», содержащих не менее одной буквы, можно составить из двух букв «а», пяти «б» и девяти «в» ?
Решение. Рассуждая так же, как в предыдущей задаче, имеем: 3*6*10-1=179
5. На окружности выбраны десять точек. Сколько можно провести хорд с концами в этих точках? Сколько существует треугольников с вершинами в этих точках? Сколько выпуклых десятиугольников?
Решение. Так как порядок выбора двух точек в качестве концов хорд и трех точек – вершин треугольников, не важен, то хорд — 

6. а) Сколькими способами из девяти книг можно отобрать четыре?
б) Сколькими способами это можно сделать, если в число отобранных должна входить некая определенная книга?
в) Сколькими способами можно отобрать четыре книги так, чтобы в число отобранных не входила определенная книга?
Решение. Рассуждая так же, получим: а)
б) так как определенная книга всегда должна входить в выбор, то недостающие три книги выбираем из восьми оставшихся, поэтому:
в) выбор будет осуществляться из восьми оставшихся книг, поэтому —
7. Десять кресел поставлены в ряд. а)Сколькими способами на них могут сесть два человека?
б) Сколькими способами эти два человека могут сесть рядом?
Решение. а) Так как неважно, в каком порядке сядут два человека, то способов – 
б) Поскольку эти двое должны сидеть рядом, то будем считать их за одного, сидящего на двух креслах . Пар кресел, расположенных рядом, (1-2, 2-3, 3-4, 4-5, 5-6, 6-7, 7-8, 8-9, 9-10) – 9 . Следовательно, способов выбора тоже 9. По другому, 
8. Сколько чисел, заключающихся между 1000 и 9999, содержат цифру 3?
Решение. Переформулируем задачу: сколько существует четырехзначных чисел, содержащих в своей записи цифру 3? Всего четырехзначных чисел – 9*10*10*10. Таких, в записи которых тройка стоит на первом месте – 10*10*10, на втором месте – 9*10*10 (т.к. «0» не может стоять на первом месте), на третьем – 9*10*10, на четвертом – 9*10*10. Всего 10*10*10+9*10*10+9*10*10+9*10*10 чисел.
9. Сколько четырехбуквенных «слов» можно образовать из слова «сердолик»? Сколько среди них таких, которые не содержат букву «р»? Сколько таких, которые начинаются с буквы «е» и оканчиваются буквой «р»?
Решение. Слово содержит 8 букв. Порядок букв в словах важен, поэтому всего четырехбуквенных слов – 8*7*6*5.
Таких, которые не содержат букву «р», — 7*6*5*4, поскольку выбор делается из семи оставшихся букв.
Таких, которые начинаются с буквы «е» и оканчиваются буквой «р», — 6*5, так выбор второй буквы делается из шести оставшихся, а третьей – из пяти оставшихся.
10. Сколько шестизначных цифр можно образовать из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, если каждое число должно состоять из трех чётных и трёх нечётных цифр, причём никакая цифра не входит в число более одного раза?
Решение. Выбираем три четных составляющих: поскольку четных цифр – 4, то возможностей – 4*3*2, а нечетных – 5, поэтому выборов – 5*4*3; Всего, согласно правила умножения – (4*3*2)*(5*4*3) выборов.
11. В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает из неё яблоко или апельсин, после чего Надя берет и яблоко, и апельсин. В каком случае Надя имеет большую свободу выбора, если Ваня взял яблоко или если он взял апельсин?
Решение. Надя имеет большую свободу выбора, если у неё больше вариантов выбора. Поэтому считаем варианты:
если Ваня взял яблоко, то остается 11 яблок и 10 апельсинов и для Нади, по правилу умножения, есть 11*10 вариантов выбора;
если Ваня взял апельсин, то остается 12 яблок и 9 апельсинов и для Нади есть 12*9 вариантов. Остается сравнить эти числа: ясно, что 12*9 9
Источник
II. На использование формул для перестановок и размещений
Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять:
(а) из восьми букв, (б) из семи букв, (в) из трех букв?
В слове фрагмент 8 букв алфавита.
(а) Всевозможные перестановки 8 букв по восьми местам: А

(б) Размещения 8 букв по 7 местам: А
(в) Размещения 8 букв по 3 местам: А
Ответ: P8, А

Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, а) если первая из них не равна нулю; б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?
а) Всего существует 10 цифр. На первом месте не может быть цифры 0, поэтому способов поставить цифру на первое место существует 9. На втором месте может стоять любая из 10-ти цифр (цифры могут повторяться), т.е. способов поставить цифру на второе место существует 10, и т.д. Используя принцип умножения, получаем: 9






б) На первом месте может стоять любая из 26 букв. На остальных местах — любые из девяти цифр, причем они могут повторяться. Используя принцип умножения, получаем: 26





Ответ: 9



Сколькими способами можно расставить на полке семь книг, если (а) две определенные книги должны всегда стоять рядом, (б) эти две книги не должны стоять рядом?
(а) Книги, которые должны стоять рядом, считаем за одну книгу. Тогда нужно расставить 6 книг по шести местам. Применяя формулу перестановок, получаем: P6 = 6!. Мы учли перестановки шести книг, не учитывая порядок внутри тех книг, которые мы посчитали за одну. А так как две книги по двум местам можно разместить только двумя способами (P2), то получаем окончательно следующее произведение: P2

(б) Способов переставить 7 книг существует P7= 7!. Из них ‑ 2

Ответ: 1440; . 7! ‑ 2
III. На использование формул для сочетаний
Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?
Для решения этой задачи необходимо использовать формулу для сочетания элементов, т.к. здесь не имеет значения порядок элементов в выборке. Запишем формулу для сочетаний и произведем вычисления:
С

Компания из двадцати мужчин разделяется на три группы, в первую из которых входят три человека, во вторую — пять и в третью — двенадцать. Сколькими способами они могут это сделать? (Ответ записать в виде произведения сомножителей, не вычисляя его.)
Из 20-ти элементов необходимо сделать три выборки, причем порядок внутри выборок значения не имеет. Поэтому используем формулу для сочетаний. Чтобы выбрать из 20-ти элементов 3, существует С




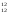
Ответ: С


Сколькими способами можно отобрать несколько фруктов из семи яблок, четырех лимонов и девяти апельсинов? (Мы считаем, что фрукты одного вида неразличимы.)
Т.к. фрукты одного вида неразличимы, то существует один способ взять одно яблоко, один способ взять 2 яблока, один способ взять три яблока и т.д., т.е. всего семь способов выбрать несколько яблок (несколько – это не менее одного). Необходимо также прибавить один способ не взять ни одного яблока. Следовательно, существует 8 способов взять яблоки. Аналогично существует 5 способов выбрать лимоны и 10 способов выбрать апельсины. Следуя принципу умножения, получим все способы отбора фруктов: 7



Источник











