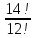Сколькими способами можно обозначить данный вектор используя буквы klmnpq

Олимпиада по математике и статистике (1 тур)

Бинарная олимпиада по дисциплинам ЕН.01 «Математика» и ОП.02 «Статистика» для студентов специальностей экономического профиля, изучающих данные дисциплины.

Олимпиада проводится в 2 тура.

Задания 1 тура представлены в двух вариантах и состоят из 10 вопросов и задач.

• Задание 1 максимально оценивается в 5 баллов;
• Задания 2 — 7 – по 1 баллу;
• Задания 8 — 10 – по 2 балла.

Общее максимальное количество баллов за 1 тур – 17 баллов.

Во второй тур проходят 10 студентов, набравших наибольшее количество баллов по итогам проведения первого тура.

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10-11 кл. Учебник для общеобразовательных учреждений. — М.:Просвещение, 2014.
2. Алгебра : элементы статистики и теории вероятностей : учеб. пособие для учащихся 7 – 9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. – 6-е изд. – М : Просвещение, 2008. – 78 с. : ил.
3. Статистика. Краткий курс лекций и тестовые задания : учебное пособие / Е.М. Мусина. – М. : ФОРУМ, 2009. – 72 с.

Просмотр содержимого документа
«Олимпиада по математике и статистике (1 тур)»

Олимпиада по математике и статистике

1. Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры 6, 7, 8, 9?

2. Сколькими способами могут занять места 5 учащихся за пятью одноместными партами?

3. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?

4. Покупатель из имеющихся в питомнике 10 саженцев хочет выбрать 2. Сколькими способами он может это сделать?

5. Вычислить:

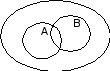
Из колоды карт вынимается одна карта. Пусть событие А – изъятие из колоды карты с картинкой, В – изъятие карты червовой масти. Пояснить, в чем заключаются события: А+ В, АВ.

События А и В изображены с помощью кругов Эйлера. Большим кругом изображены все элементарные исходы испытания, с которыми связаны события А и В. С помощью штриховки проиллюстрировать событие, состоящее в том, что произошли оба события А и В.

Какова вероятность, что при изъятии одной карты из колоды в 36 карт игрок вынет короля пик?

а) 1/36 б) 1/18 в) 1/9 г) 2/9

Брошены две игральные кости. Найти вероятность того, что на первой кости выпало число 2, а на второй – нечетное число.

а) 1/36 б) 1/12 в) 1/6 г) 1/18

Формулу средней геометрической величины целесообразно применять, если:

информация задана в виде произведений вариантов и частот (объемов явлений);

значения вариантов повторяются;

необходимо рассчитать средний темп роста;

значения вариантов не повторяются.

Найти размах, моду, медиану и среднее выборки -1, 12, -6, -7, 13, -2, 10, -2, -9.

Таблица частот характеризует наличие бракованных деталей в контрольной партии ящиков. Восстановите пропущенные значения, зная, что ящиков с двумя бракованными деталями вдвое больше, чем с тремя, а в среднем в каждом ящике по 1,85 бракованных деталей.

Источник

Презентация по математике на тему «Элементы комбинаторики»

Описание презентации по отдельным слайдам:

Элементы комбинаторики Преподаватель: Перминова Е.В. ГБПОУ СО «Свердловский педагогический коллеж»

Факториал. Таблица факториалов: Определение. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Обозначение n! n 0 1 2 3 4 5 6 7 8 9 10 n! 1 1 2 6 24 120 720 5 040 40 320 362 880 3 628 800

Перестановками из n элементов называются соединения (комбинации), которые состоят из одних и тех же n элементов и отличаются одно от другого только порядком их расположения. Задача 1: Сколькими способами можно поставить рядом на полке 4 различные книги? Ответ: 24 Х Х Х Определение. Решение: 4 3 2 1 = 24

Перестановки с повторениями. Определение . Число перестановок n – элементов, в котором элементов i –того типа ( ) вычисляется по формуле Задача: Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»? Решение: экзамен – 7 букв ( без повт.) , Математика — 10 букв ( с повт. м=2,а=3,т=2,е=и=к=1) ,

Пример 1. Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках? Решение: P8 = 8! = =40 320 Пример 2. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, причём в каждом числе цифры должны быть разные? Решение: P4 = 4! = =24, Р4 – Р3 = 4! – 3! = 18 P3 = 3! = =6,

Размещения с повторениями. Определение. k – размещением с повторениями n–элементного множества называется упорядоченный набор длины k элементов данного множества. Пример. 2- размещения с повторениями: Число k – размещений с повторениями вычисляется по формуле: Задача: Сколько существует номеров машин?

Сочетание и их свойства

Равенство: Число размещений, перестановок и сочетаний связаны равенством:

порядок важен порядок неважен сочетания перестановки размещения Схема связи:

Учимся различать виды соединений. Pn Перестановки изnэлементов Сколькими способами можно с помощью букв A,B,C,D обозначить вершины четырехугольника? Меняется только порядок расположения выбранных элементов Сочетания изmэлементов поnэлементов У лесника три собаки: Астра, Вега и Граф. На охоту лесник решил пойти с двумя собаками. Перечислите все варианты выбора лесником пары собак. Меняется только состав входящих в комбинацию элементов, порядок их расположения не важен Размещения из mэлементов поnэлементов Сколькими способами могут быть распределены I, II и III премии между 15-ю участниками конкурса? Меняется состав входящих в комбинацию элементов и важен порядок их расположения

«Би»-удвоение, раздвоение … «Ном»(фран. nombre) –номер, нумерация. «Бином» -»два числа» Бином Ньютона – это выражение вида Треугольником Паскаля пользуются при возведении бинома в натуральные степени. Бином Ньютона.

Треугольник Паскаля столбцы строки 0 1 2 3 4 5 6 … 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 … …

Различие между перестановками, размещениями, сочетаниями В случае перестановок берутся все элементы и изменяется только их местоположение. В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга. В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.

Проверь себя Что такое комбинаторика? В чём состоит правило суммы? В чём состоит правило произведения? Что такое размещения? Запишите формулу для нахождения числа размещений. Что такое перестановки? Запишите формулу для нахождения числа перестановок. Что такое факториал? Что такое сочетания? Запишите формулу для нахождения числа сочетаний. В чём различие между перестановками, размещениями, сочетаниями?

Задача: 2 способ: дерево возможных вариантов. Для этой задачи построена специальная схема. Ставим звездочку. Далее отводим от звездочки 3 отрезка. Так как в условии задачи даны 3 цифры – 1, 4, 7, то на концах отрезков ставим цифры 1, 4, 7. Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола Ответ: 6 чисел. **

Задача 1 Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3? Решение: m = 3, n = 4; Ответ: 12 Задача 2 Сколько различных трехзначных чисел можно записать с помощью цифр 0, 1, 2, 3? Решение: m=3, n=4, k=4; Ответ: 48 Задача 3 Сколько различных пятибуквенных слов можно записать с помощью букв «и» и «л»? Решение: a = 2, b = 2, c = 2, d = 2, f=2; Ответ: 32 = 32 Л и л и и 2 • 2 • 2 • 2 • 2 = abcdf = m • n = 12 mnk=3 • 4 • 4 =48

Упражнения: № 1043 Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры: 1вариант: 1) 1, 2 и 3; 3) 5, 6, 7 и 8; 5) 0, 2, 4 и 6; 2 вариант: 2) 4, 5, и 6; 4) 6, 7, 8 и 9; 6) 0, 3, 5 и 7? Ответ: 1), 2) 6; 3), 4) 12; 5), 6) 9. Сколько различных трехзначных чисел можно записать с помощью цифр: 1 вариант: 1) 2 и 3; 3) 0 и 2; 2 вариант: 2) 8 и 9; 4) 0 и 5? Ответ: 1), 2) 8; 3),4) 4. № 1044 № 1 в учебнике — № 1043; № 2 в учебнике — № 1044. Знак вопроса в квадрате – гиперссылка на решение упражнения №1. Буква i в круге и квадрате – гиперссылка на информацию о подобном решении задачи № 3 (о лилиях)

№ 1045 Сколько различных трехзначных чисел, не имеющих одинаковых цифр, можно записать с помощью цифр: 1 вариант: 1) 3, 4 и 5; 3) 5, 6, 7 и 8; 2 вариант: 2) 7, 8, и 9; 4) 1, 2, 3 и 4? Ответ: 1),2) 6; 3),4) 24. № 146 Сколько различных четырехбуквенных «слов» можно записать с помощью букв: 1 вариант: 1) «м» и «а»; 3) «к», «а» и «о»; 2 вариант: 2) «п» и «а»; 4) «ш», «а» и «л». Ответ: 1), 2) 16; 3), 4) 81. С.Р. № 3 в учебнике — № 1045; № 4 в учебнике — № 1046. С.Р.(на полях) – самостоятельная работа.

№ 147 Путешественник может попасть из пункта А в пункт С, проехав через пункт В. Между пунктами А и В имеются три различные дороги, а между пунктами В и С — четыре различные дороги. Сколько существует различных маршрутов между пунктами А и С? Решение: m = 3, n = 4; mn = 3•4 = 12 Ответ: 12 А В С № 5 в учебнике — № 1047

№ 1048 Чтобы попасть из города М в город К, нужно проехать через город N. Между городами М и N имеются четыре автодороги, а из города N в город К можно попасть либо поездом, либо самолетом. Сколько существует различных способов добраться из города М в город К? Ответ: 8 С.Р. Дополнительно № 6 в учебнике — № 1048. «Дополнительно» – гиперссылка к дополнительным задачам к уроку. Треугольник в квадрате на полях – гиперссылка на новую тему: «Перестановки».

№ 1064 Упростить формулу записи выражений (полагая, что k-натуральное число, k>4) 1) 3) 5)

Упростить формулу записи выражений (полагая, что k-натуральное число, k>6) Упражнения: № 1 № 2 Ответ: 11!; 18!. Ответ: 22!; 27!. № 3 Ответ: (k+1)!; k!.

Перестановки Сочетания и их свойства Размещения

Число перестановок: (1) Произведение первых n натуральных чисел обозначают n! (читается «эн факториал») n! = 123(n –2)(n–1)n Pn = n(n –1)(n – 2)321 (2) Pn = n! (3)

№ 1059 Найти значение: 1) P5 = 5! = 5 4 3 2 1 = 120; № 1060 Сколькими способами можно рассадить четверых детей на четырех стульях в столовой? № 1063 Сколько различных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 1,2,3,4,5 так, чтобы: 1) последней была цифра 3; 3) первой была цифра 5, а второй – цифра 1; 5) первыми были цифры 3 и 4, расположенные в любом порядке? Упражнения: №№ 1064 — 1071 2) P7 ; 3) P9 ; 4) P8 .

Пример 3. Имеется 10 различных книг, среди которых есть трёхтомник одного автора. Сколькими способами можно расставить эти книги на полке, если книги трёхтомника должны находиться вместе, но в любом прядке? Решение:

Задача 1. Сколько различных двузначных чисел можно записать с помощью цифр 1, 2, 3, 4 при условии, что в каждой записи нет одинаковых цифр? Решение: 1 способ – решение перебором: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43. 2 способ – по правилу произведения: m = 4, n = 3; mn = 12 Ответ: 12 Из задачи видно, что любые два соединения отличаются либо составом элементов (12 и 24), либо порядком их расположения (12 и 21). Такие соединения называют размещениями.

Размещениями из m элементов по n элементов (n ≤ m) называются такие соединения, каждое из которых содержит n элементов, взятых из данных m разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения. Обозначение:  читают «А из эм по эн»: = 12.

= m(m – 1)(m – 2) • … • (m – (n – 1)) Примеры: = 4 • 3 = 12; = 4 • 3 • 2 = 24; = 5 • 4 • 3 = 60 = Задача 2. Сколькими способами можно обозначить данный вектор, используя буквы A, B, C, D, E, F? Решение: (1) (2) или

Вычислить: Задача 5 Ответ: 225 Упражнения: № 1073 – № 1075

Задача 5. Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать? Решение:

Задача 6. Сколько существует семизначных телефонных номеров, в которых все цифры различны и первая цифра отлична от нуля? Решение: Задача 7. Сколько существует трёхзначных чисел, составленных из цифр 1, 2, 3, 4, 5, 6 (без повторений), которые НЕ кратны 3? Решение:

Определение. Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание).

Пример 1. Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек? Решение:

Пример 2. Из вазы с цветами, в которой стоят 10 красных гвоздик и 5 белых, выбирают 2 красные гвоздики и одну белую. Сколькими способами можно сделать такой выбор букета? Решение:

Пример 3. Семь огурцов и три помидора надо положить в два пакета так, чтобы в каждом пакете был хотя бы один помидор и чтобы овощей в пакетах было поровну. Сколькими способами это можно сделать? Решение:

2) Число всех членов разложения на единицу больше показателя степени бинома, то есть равно (n+l). 3) Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома, то есть n. 4) Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой: (правило симметрии). Свойства бинома и биномиальных коэффициентов.

5) Сумма биномиальных коэффициентов всех членов разложения равна . 6) Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна 7) Правило Паскаля: . Свойства бинома и биномиальных коэффициентов.

8)Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби . Свойства бинома и биномиальных коэффициентов.

Пример . Доказать, что при любом натуральном n число делится на 9. Доказательство: Начнем рассматривать бином в общем виде: Тогда

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 … … Треугольник Паскаля

О пользе комбинаторики или лишних знаний не бывает

1. 2. отгадай ребусы

3. 4. 5. отгадай ребусы

Ответы: Вариант Сочетания Факториал Событие Исход

Спасибо за внимание!

Д/З: § 60, №№ 1051, 1055. Д/З: § 61, № 1063 (четные) Д/З: § 62, № 1072, 1076

Электронные ресурсы: кубики: http://free-math.ru/load/prezentacii_egeh_po_matematike/verojatnost_i_kombinatornoe/38-1-0-173 лилии: http://ru.gde-fon.com/cvety?offset[0]=648 http://ru.gde-fon.com/cvety?offset[0]=666 http://ru.gde-fon.com/cvety?offset[0]=4590 шаблон: http://www.myshared.ru/slide/56405/ Санкт-Петербург, 2014

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 832 человека из 77 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 297 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 609 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

Настоящее методическое пособие в первую очередь нацелено на оказание методической помощи учителям математики, приступающим к преподаванию теории вероятностей и статистики. Обращается внимание учителя на наиболее важные вопросы курса и на связи между ними. Даны решения и способы записи наиболее важных типовых задач. Большой объем практических заданий поможет учащимся без труда освоить основы комбинаторики. Материал, изложенный в пособии, может быть полезен и школьным учителям при подготовке к урокам, и преподавателям методики обучения математике в школе, и родителям учащихся.

Математика – это то, посредством чего люди управляют природой и собой.

Номер материала: ДБ-1391794

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

Спортивные и творческие кружки должны появиться в каждой школе до 2024 года

Время чтения: 1 минута

С 2019 года закрыто более 50 детских лагерей

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник