Сколько существует способов добраться из исходной точки до правого верхнего угла
Имеется клетчатое поле размером m × n. В левом нижнем углу сидит черепашка. Она умеет ходить только вправо или вверх. Перед тем как добраться до правого верхнего угла её заинтересовал вопрос: сколько существует способов добраться из исходной точки до правого верхнего угла?
Входные данные
Два натуральных числа m и n, не превышающие 30.
Вывести количество способов, которыми черепашка сможет добраться из левого нижнего угла в правый верхний.

Всем привет! Недавно решал одну любопытную задачу, но к сожалению не смог решить на 100%. Вот.
Нарисовать движущуюся от левого нижнего угла экрана до правого верхнего угла окружность
Нарисовать, движущуюся от левого нижнего угла экрана до правого верхнего угла.
Бегущая из верхнего правого угла строка
Создать бегущую из верхнего правого угла строку, совершающую каждую секунду перемещение на один.

заполнение матрицы по спирали начиная с перхнего правого угла Добавлено через 18 часов 29 минут.
Источник
Преподавание теории вероятности и статистики в школе.Первые уроки.

Математический кружок.»Комбинаторика».первые уроки.Решение задач.
Просмотр содержимого документа
«Преподавание теории вероятности и статистики в школе.Первые уроки.»
Из города А в город B ведут 2 дороги, а из города B в город С ведут 4 дороги. Каким числом способов можно проехать из города A в город С? А если из города А в город В ведёт 3 дороги?
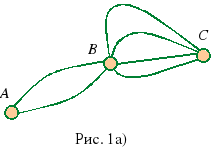
Сколькими способами можно проехать из города A в город С, если схема дорог следующая:
а) В прихожей стоят 2 левых и 3 правых сапога, все пять разного цвета. Сколькими разными способами можно обуться, надев один левый и один правый сапог?
б) Тот же вопрос, если в прихожей стоят 5 левых и 13 правых сапог.
Из города А в город B ведут 3 дороги, а из города B в город С ведёт 5 дорог. Какие дороги можно закрыть, чтобы число способов проехать из города A в город С стало равно 9?
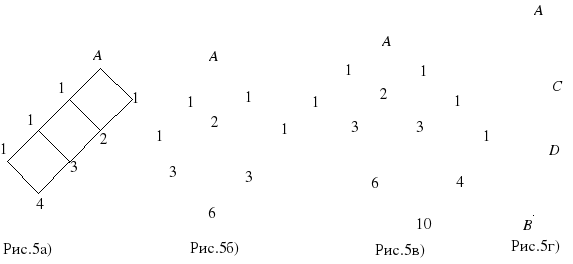
В точке A сидит математический паук. Ему удается двигаться по паутине только вниз. Сколькими способами он может пробраться в точку B, если паутина имеет вид:
Паук из задачи 5 сплёл следующие паутины (см. рисунки). Сколькими способам теперь он может пробраться из точки A в точку В?
У мамы в коллекции 31 вазочка (все вазочки разные). Из них 10 красных, 8 синих, 8 зелёных и 5 жёлтых. Папа разбил три вазочки. Он позвонил маме по телефону и сообщил, что разбил три вазочки, все – разного цвета. После чего сразу же повесил трубку. Сколько различных гипотез о том, какие именно вазочки разбиты, может построить мама (дозвониться до папы ей не удаётся)?
а) В левой нижней клетке прямоугольника 215 сидит математическая черепаха. За один ход она умеет двигаться на одну клетку вправо или на одну клетку вверх. Каким числом способов она может добраться до правой верхней клетки?
б) Тот же вопрос для прямоугольника 315.
Каким числом способов можно нарисовать в строчку
а) один крестик и 14 ноликов? б) 2 крестика и 14 ноликов?
Математическая черепаха сидит в левой нижней клетке прямоугольника 3n. Докажите, что количество способов, которыми она может добраться до правого верхнего угла, равно количеству способов нарисовать в строчку 2 крестика и n – 1 нолик.
Это первое занятие по теме «комбинаторика». На этом занятии ребята должны научиться правилам «умножения» и «сложения» – научиться понимать, когда способы надо перемножать, а когда – складывать. Никаких формальных правил здесь мы не формулируем. Ребята должны просто прочувствовать это, решая конкретные задачи.
Задачу 5 дети, скорее всего, будут решать перебором (перечислением всех вариантов). Это нормально, такие решения надо засчитывать. Однако прежде чем перейти к следующей задаче, полезно рассказать «программный» метод решения на примере какого-нибудь пункта задачи 5. В шестой задаче переборные решения лучше не принимать. Для этого достаточно попросить ребенка доказать, что он перечислил все варианты, что других нет.
Разберем, например, пункт 5б.
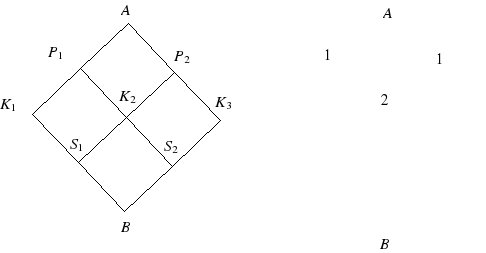
Будем в каждую точку ставить число – сколькими способами до нее можно добраться. Очевидно, что в точки P1 и P2 можно дойти только одним способом. Напишем туда 1. В точку К2 можно придти из точки P1 или из точки P2, всего 2 способа.
Очевидно, что до К1 и К3 тоже можно добраться только одним способом.
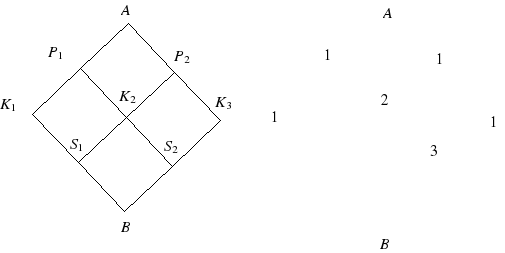
Посмотрим, какие пути ведут точку S2. Они делятся на пути, идущие до точки K2, а потом по отрезку K2S2, и пути, идущие до точки K3, а потом по отрезку K3S2. (Из других точек нельзя пойти непосредственно в S2.)
До точки K2 мы можем дойти двумя способами, значит, прийти в S2 через K2 мы можем тоже двумя способами. Прийти в S2 через K3 мы можем одним способом. Всего три способа прийти в S2.
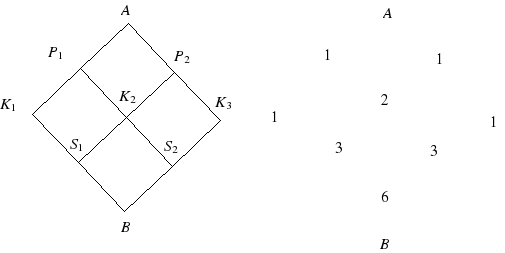
Аналогично до S1 есть три пути.
В точку B мы можем придти только из точек S1 и S2. Поэтому все пути до В делятся на пути, идущие до B через S1 и идущие до B через S2.
До S1, как мы уже выяснили, можно дойти 3 способами, поэтому через точку S1 в B ведут 3 пути и еще 3 через точку S2, итого 6.
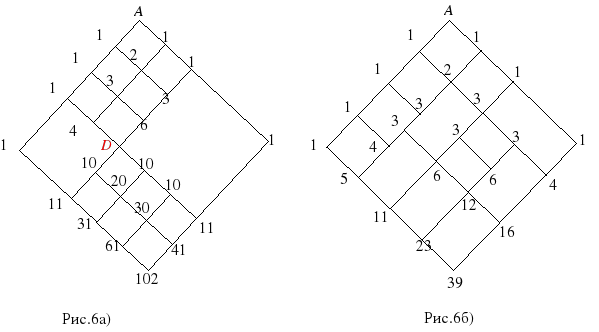
(Буквенные обозначения узлов введены для удобства изложения. На занятии можно не вводить никаких букв, а писать только цифры – количество способов дойти до вершины.)
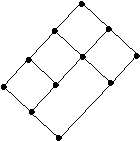
Далее стоит нарисовать еще одну картинку, например такую
и уже силами детей расставить цифры во все узлы по порядку, как описано выше (чтобы они с места подсказывали, какую цифру поставить в данный узел).
Из города А в город B ведут 2 дороги, а из города B в город С ведут 4 дороги. Каким числом способов можно проехать из города A в город С? А если из города А в город В ведёт 3 дороги?
Решение. а) Из А до В можно доехать по 2 дорогам. Если мы до В ехали по первой, то у нас есть 4 варианта продолжить путь до С. Если же до В мы ехали по второй дороге, то у нас опять 4 способа продолжить свой путь до С. Итого
4 + 4 = 8 способов.
б) До города В можно доехать 3 путями. В конце каждого из них у нас выбор из 4 дорог для продолжения пути. Итого 4 + 4 + 4 = 12 способов.
Сколькими способами можно проехать из города A в город С, если схема дорог следующая:
Решение. а) Можно ехать через В, либо через D. Через B можно проехать 3 4 = 12 способами. Через D можно проехать 2 3 = 6 способами. Общее количество путей равно сумме путей через B и D.
б) От А до В можно доехать по двум дорогам. Пусть мы поехали по первой. Тогда у нас есть 3 4 = 12 способов доехать от B до C (см. задачу 1б). Точно так же, если мы из А в B поедем по второй дороге, дальше у нас будет снова 12 способов проехать оставшийся путь из В в С. Итого 12 + 12 = 24 способа.
в) В самом начале придется выбрать: ехать через E, через B или через F.
Доехать из А в С через Е 2 1 = 2 способа.
Доехать из А в С через В 3 4 3 = 36 способов.
Доехать из А в С через F 2 3 3 = 18 способов.
Всего 2 + 36 + 18 = 56 способов.
а) В прихожей стоят 2 левых и 3 правых сапога, все пять разного цвета. Сколькими разными способами можно обуться, надев один левый и один правый сапог?
б) Тот же вопрос, если в прихожей стоят 5 левых и 13 правых сапог.
Решение. а) Если мы надели один левый, то в пару ему можно выбрать любой из трех правых. Т.е. 3 + 3 = 6 способов.
б) 5 13 = 65 способов.
4. Из города А в город B ведут 3 дороги, а из города B в город С ведёт 5 дорог. Какие дороги можно закрыть, чтобы число способов проехать из города A в город С стало равно 9?
Решение. Т.к. количество путей равно произведению числа дорог из А в В на число дорог из В в С, то нам нужно представить 9 как произведение двух сомножителей. 9 представляется в таком виде двумя способами: 9 = 1 9 и 9 = 3 3. Так как число дорог увеличивать нельзя, то мы не можем сделать так, чтобы из А в В или из В в С вело 9 дорог, т.е. первый случай не реализуется. А вот сделать так, чтобы из А в В и из В в С вело по 3 дороги мы можем – для этого достаточно закрыть любые две дороги, ведущие из В в С.
Ответ: Можно закрыть любые две дороги, ведущие из В в С.
В точке A сидит математический паук. Ему удается двигаться по паутине только вниз. Сколькими способами он может пробраться в точку B, если паутина имеет вид:
Ответ: а) 4; б) 6; в) 10; г) 216.
Решение. г) Заметим, что из А в В можно дойти 6 способами, из С в D – тоже шестью, и из D в B тоже 6. Как в задаче 2б), получаем, что всего способов 6 6 6 = 216.
Паук из задачи 5 сплёл следующие паутины (см. рисунки). Сколькими способам теперь он может пробраться из точки A в точку В?
а) Решение. Тут можно последовательно найти число способов дойти до каждого узла, а можно заметить, что это дойти из А до D, а потом от D до В и плюс два способа через правую и левую вершины квадрата: 10 10 + 2 = 102.
У мамы в коллекции 31 вазочка (все вазочки разные). Из них 10 красных, 8 синих, 8 зелёных и 5 жёлтых. Папа разбил три вазочки. Он позвонил маме по телефону и сообщил, что разбил три вазочки, все – разного цвета. После чего сразу же повесил трубку. Сколько различных гипотез о том, какие именно вазочки разбиты, может построить мама (дозвониться до папы ей не удаётся)?
Решение. Всего 4 варианта распределения по цветам:
красный, синий, зеленый (ксз)
красный, синий, желтый (ксж)
красный, зеленый, желтый (кзж)
синий, зеленый, желтый (сзж).
Если папа разбил одну красную, одну синюю и одну зеленую вазочку, то таких вариантов всего будет 10 8 8 = 640. Далее, если это ксж, то вариантов 10 8 5 = 400, если это кзж, то 10 8 5 = 400. Если сзж, то 8 8 5 = 320. Итого 640 + 400 + 400 + 320 = 1760.
Ответ: 1760 различных гипотез.
а) В левой нижней клетке прямоугольника 215 сидит математическая черепаха. За один ход она умеет двигаться на одну клетку вправо или на одну клетку вверх. Каким числом способов она может добраться до правой верхней клетки?
б) Тот же вопрос для прямоугольника 315.
а) Ответ: 15 способов.
Решение. Путь черепахи состоит из нескольких ходов вправо, потом хода вверх, потом до конца вправо. Т.е. способ определяется тем, в какой клетке она пошла вверх. Вверх она может пойти сразу же, во второй клетке, в третьей и т.д. в 15-й, т.е. всего 15 вариантов.
б) Ответ: 120 различных путей.
Решение. Способ первый. Можно заметить, что черепаха – это повернутый математический паук. Т.е. в каждой клетке мы можем записать число – сколькими способами черепаха может добраться до этой клетки. Заполнив все клетки, получим, что до угловой она может добраться 120 способами.
Способ второй. Заметим, что путь черепахи состоит из 16 ходов, из которых два хода вверх и 14 ходов вправо. Пути определяются тем, на каком именно ходу черепаха сделает ходы вверх. Если она первым же ходом пошла вверх, то второй ход вверх она может сделать из любой из 15 клеток второй строчки, т.е. в этом случае 15 способов продолжить свой путь. Если в первый раз черепаха пошла вверх из 2-й клетки, то сделать второй ход вверх у нее будет уже 14 способов. И так далее. Всего получается
15 + 14 + 13 + 12 + … + 2 + 1 = 120
Каким числом способов можно нарисовать в строчку
а) один крестик и 14 ноликов? б) 2 крестика и 14 ноликов?
Решение. См. решение задачи 8б).
а) 15 (у нас всего 15 символов и нам нужно выбрать место, на котором будет стоять нолик).
б) Последовательности из 14 ноликов и двух крестиков кодируют всевозможные пути черепахи из левого нижнего в правый верхний угол на доске 315 (крестик означает, что на этом ходу черепаха делает ход вверх), т.е. ответ такой же, как в задаче 8б) – всего 120 способов.
Количество таких строчек можно было посчитать и следующим образом: у нас есть 16 позиций. Количество способов заполнить их 14 ноликами и 2 крестиками равно числу способов выбрать из них 2 места, на которых будут стоять крестики. Первое место мы можем выбрать любое из 16 – т.е. 16 способами, а второе – любое из оставшихся 15 – это 15 вариантов.
Т.е. всего выбрать место для первого крестика, а потом для второго мы можем 15 16 = 240 способами. При этом каждый вариант мы посчитали два раза (например, вариант «первый крестик поставить на 5 место, а второй на 7 место» = варианту «первый крестик поставить на 7 место, а второй – на 5 место»). Поэтому получившееся число способов надо разделить на 2. Итого 240 : 2 = 120.
Математическая черепаха сидит в левой нижней клетке прямоугольника 3n. Докажите, что количество способов, которыми она может добраться до правого верхнего угла, равно количеству способов нарисовать в строчку 2 крестика и n – 1 нолик.
Решение. См. соответствие, построенное в задаче 9б).
Источник