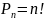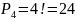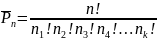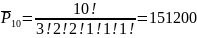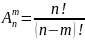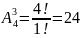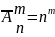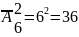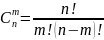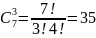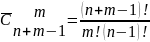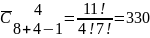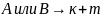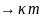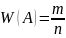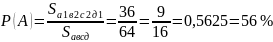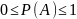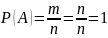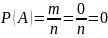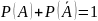Сколькими способами могут взойти 3 зерна пшеницы если посажено 7 зерен
Основоположник теории множеств… Объекты, входящие во множество, называют … и обозначают… Назвать операции над множествами… Объединение (сумма) множеств…. Показать с помощью кругов Эйлера. Мощность множества… Записать формулу числа размещений. Сколько элементов содержится во множестве: А=<2,5,9,11>; B= <1547]; C=<1,4,7,23,145,660,10000>Равны ли множества
Какое из соотношений записано, верно?
8
<5,4,9,8,12>; 11
Сколькими способами могут взойти 3 зерна пшеницы, если посажено 7 зерен? Укажите множество действительных чисел, соответствующих записи:
Составьте различные новые слова из букв слова: норматив.
Понятие множества… Обозначение множеств и способы задания… Кортеж… Пересечение множеств…. Показать с помощью кругов Эйлера. Виды множеств… Записать формулу числа сочетаний. Сколько элементов содержится во множестве: А=<1,5,9,11, 21>; B=
Равны ли множества
Какое из соотношений записано, верно?
12
<5,4,9,8,12>; 9
Сколькими способами из различных нечетных цифр можно составить различные трехзначные числа? Укажите множество действительных чисел, соответствующих записи: А=
> Составьте различные новые слова из букв слова: стадион.
Источник
Разработка по математике на тему: «Комбинаторика»
Прикладной аспект теории связан с необходимостью подсчитывать количества различных объектов, учитывая или не учитывая их порядок. Например, метеорологу для составления прогноза погоды на 10 января этого года приходится анализировать не только характер последних данных о природных явлениях, но и варианты характеристик погоды на 10 января в предыдущие годы.
Раздел математики, занимающийся подсчётами количества различных комбинаций между объектами, называется комбинаторикой.
Группы, составленные из каких–либо элементов, называются соединениями.
Различают три основных вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными.
Раздел математики, занимающийся их решением, называется комбинаторикой.
Рассмотрим три вида соединений.
Перестановками из n элементов называются такие соединения из n элементов, которые отличаются друг от друга лишь порядком их следования.
Число перестановок из n элементов обозначается символом: и вычисляются по формуле:
Произведение, первых натуральных чисел, обозначается: — «э п-факториал» , причем можно записать:
1.На собрании пожелали выступить 4 человека. Сколькими способами можно расположить список докладчиков?
2.Сколько шестизначных чисел, кратных пяти, можно составить из цифр1,2,3,4,5,6 при условии, что в числе цифры не повторяются?
Решение: цифра 5 должна стоять на последнем месте (кратные пяти). Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке, .
Размещениями из n элементов по m называются такие соединения, которые
отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их следования.
Число размещений из n элементов по m обозначаются символом: и вычисляется по формуле:
В группе 20 студентов. Сколькими способами могут быть выбраны староста и его заместитель при условии, что каждый студент может быть выбран только на одну должность?
Группа изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 3 различных пары?
Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4?
Решение: . Итого 12+4=16.
Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4?
Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4 при условии, что в каждом числе нет одинаковых цифр?
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить 4 фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Сочетаниями из n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по m обозначается символом и вычисляется по формуле:
Группу студентов колледжа должны экзаменовать по математике комиссия из двух преподавателей. Сколькими способами может быть составлена такая комиссия, если в колледже пять преподавателей математики?
Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?
Найти число размещений:
1) из 10 элементов по 4;
2) из ( n + 4) элементов по ( n – 2).
Составить все возможные перестановки из элементов:
Вычислить значения выражений:
Ответы и решения
4. 840; 2652; 105; 16
Задача. Набирая, номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал наугад их наудачу. Какова вероятность того, что номер набран правильно?
n – Число всех исходов возможных.
При решении комбинаторных задач в первую очередь будем применять два важных правила: правило суммы и правило произведения.
Обозначения: А и В – конечное множество, n ( A ), n ( B ) – число элементов множества А и В.
Если А и В не содержит общих элементов , то
Например, если в группе 13 юношей и 12 девушек, то преподаватель может вызвать к доске одного студента 12+13 =25 способами.
Если А и В содержит общие элементы , то
Пример. Сколько человек в группе занимается спортом, если 9 человек занимаются лыжами и плаванием, а 12 человек – плаванием и волейболом, причем в секцию по плаванию ходят 4 человека из группы.
Решение. Имеем: n ( A )=9, n ( B )= 12,
Правило суммы А, В и С.
Из 35 студентов, побывавших на каникулах в Москве, все, кроме двоих, делились впечатлениями. О посещении Большого театра с восторгом вспоминали 12 человек, Кремля – 14 , а 16 – о концерте, по три студента запомнили посещение театра и Кремля, а также театра и концерта, а четверо – концерта и пребывания в Кремле. Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле?
А – число студентов, вспоминающих о театре, n ( A ) =12;
B – о Кремле, n ( B ) = 14;
C – о концерте, n (С) = 16;
D – число студентов, побывавших в поездке.
(35 – 2=33) – делились впечатлениями, обозначим через: х =
=33=12+14+16 – 3 – 3 – 4 – x ,
ОТВЕТ: Всего три студента рассказывали о трёх культурных мероприятиях поездки.
Упражнение. В результате социологического опроса студентов факультета программирования о занятиях в свободное от занятий время выяснилось, что из 100 человек:
18 – любят читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
28 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
1.Сколько студентов любят ходить в театр?
2.Сколько студентов читают книги, посещают театр, но не дискотеки?
3.Сколько студентов посещают либо дискотеки, либо театр?
4.Сколько студентов, посещая дискотеки и театр, не любят читать книги?
5.Сколько студентов предпочитают только дискотеки?
6.Сколько студентов посещают либо дискотеки, либо театр, либо читают книги?
Правило произведения. Если элемент b можно выбрать k способами, а элемент с можно выбрать m способами, то пару ( b , c ) можно выбрать km способами.
Пример. В колледже есть три варианта занятий по интересам: творческие объединения (ТО), спортивные секции (СС) и научное студенческое общество (НСО). Каждое направление содержит по четыре вида коллективов: ТО – театральный, музыкальный, танцевальный и КВН; СС – лёгкая атлетика лыжи, спортивные игры и плавание; НСО – естественно – математическое, гуманитарное, техническое и информационное направление. Сколькими способами студенты могут разнообразить свой досуг в колледже после занятий, выбрав коллектив по интересам?
Решение. Так как надо учесть и три основных направления, и то, что в каждом из них по четыре коллектива, то для подсчёта общего числа вариантов их нужно перемножить: n ( A ) = 3, n ( B ) = 4,
Частным случаем правила произведения является число размещений с повторениями .
Пример. Сколькими способами из различных нечетных цифр можно составить различные трёхзначные числа? (
Пример. Сколькими способами могут взойти 3 зерна пшеницы, если посажено 7 зёрен?
Решение, так как порядок не важен, то
Перестановки с повторениями
Если имеются соединения с повторяющимися элементами, то формула уже неприменима, так как при переставлении одинаковых элементов соединение не изменится. Соединения, имеющие повторяющиеся элементы, называются перестановками с повторениями.
1.Сколькими способами можно расставить белые фигуры на первой линии шахматной доски?
Решение: на первой линии могут находиться король, ферзь, 2 ладь, 2 коня, 2 слона. Длина 8, состав(1,1,2,2,2). Тогда число перестановок с размещениями найдём по формуле: .
Решение задач, связанных с перебором вариантов, требует анализа комбинаторных вычислений.
2.Сколько слов можно получить, переставляя буквы в слове математика?
Решение: слово имеет длину 10; состав (2;3;2;1;1;1), т. е.
«и» — 2 раза; «а» — 3 раза, «м» — 2 раза …
3.Сколько различных перестановок можно образовать из букв следующих слов: а) зебра; б) баран; в) водород; г) абракадабра.
Ответ: 120; 60; 420; 83160.
Упражнение. Составьте различные новые слова из букв слова: а) апельсин; б) норматив; в) стационар; г) ромашка; д) множества; е) ратификация.
Задачи подсчёта возможных комбинаций объектов, удовлетворяющих определённым условиям, часто встречаются в практической деятельности и получили название комбинаторных.
Многообразие таких задач не всегда удается описать с помощью математических формул. Однако для стандартных распространенных ситуаций способы подсчёта вариантов определены.
Разложить n различных деталей в m ящиков. Сколько вариантов таких размещений можно перебрать?
Решение: так как все n деталей могут поместиться и в один ящик, то на языке функции можно установить связь: между количеством n деталей и количеством ящиков m : n .
Такое часто встречающееся число подсчётов вариантов называют размещением с повторением и обозначают . Так как каждую из n деталей можно разместить в m ящиков, то необходимо n раз умножить число m , то есть .
Сколько различных двоичных чисел длиной 6 можно записать с помощью цифр 0 и 1?
Решение: размещаем две цифры 0 и 1 на 6 мест, то есть на каждом из шести мест ( m =6) может быть одна из двух двоичных цифр. Всего таких вариантов будет двоичных чисел: на каждом из шести мест по два варианта цифр.
Сколько проводится матчей в Чемпионате РФ по футболу в премьер – лиге (16 команд) за сезон?
Решение: поскольку один матч проводится между двумя командами, каждый матч состоит из двух элементов (одна команда играет дома, вторая на выезде), количество матчей вычисляется по формуле: .
Комбинаторный анализ, или комбинаторика, одна из наиболее успешно применяемых в настоящее время областей математики.
Прикладной характер комбинаторики проявляется в её применении в операционных исследованиях, в статистике и др. В операционных исследованиях она применятся для составления расписаний, определения последовательности промышленных операций, распределения материала, маршрутов транспортных средств и т. д.
Источник
1. Элементы комбинаторики. Понятие. Пример.
Комбинаторика раздел математики, занимающийся подсчетами количества различных комбинаций между объектами.
Перестановка – упорядоченные множества состоящие из n различных элементов 
Пр-р: сколько можно составить все возможных комбинаций из букв АВСД? 
Перестановка с повторениями – если множество имеет повторяющиеся элементы 
Пр-р: в слове математика: а-3, м-2, т-2, е-1, и-1, к-1 
Размещение – упорядоченное подмножество m элементов, составленное из всего множества, содержащего n элементов 
Пр-р: Сколькими способами можно распределить 3 путевки между 4мя желающими? 
Размещение с повторением – случай, когда размещение из n элемениов по m элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем. 
Пр-р: сколько различных двоичных чисел длинной 6 можно записать с помощью цифр 0 и 1? 
Сочетание из n элементов по m наз неупорядоченное подмножество, состоящее из m элементов, взятых из множества, состоящего из n элементов 
Пр-р: сколькими способами могут взойти 3 зерна пшеницы если посажено 7 зерен? 
Сочетания с повторениями – каждое сочетание с повторением из n элементов по m элементов может содержать не только из различных элементов, но и из m каких угодно и как угодно повторяющихся элементов или не содержать совсем. 
Пр-р: студент покупает 4 тет. В магазине выставлены тет 8ми видов. Сколько сущ различных способов купить 4 тет? 
2. Правило умножения и сложения комбинаторики. Пример.
Пусть элемент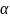 
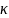
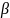
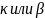
можно выбрать 
способами, а элемент 
— m способами, причем, если любой способ выбора отличается от любого способа выбора (независимо) то выбор « 
» можно сделать К+m способами.
(в группе 16 юношей и 14 девушек, то преподаватель может вызвать к доске 1 учащегося 14+16=30 способами.)
Если элемент можно выбрать способами, а элемент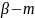 
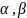
способами, то пару ( 
)можно выбрать m способами. А и В 
(всего 26 человек, м-21, ж -5, то 21*5=105 способов.)
3. Классическое и статистическое определение вероятности. Пример.
Вероятность события – это численная мера объективной возможности его появления.
Вероятность события А наз отношение числа благоприятствующих этому событию исходов к общему числу равновозможных несовместных элементарных исходов, образующие полную группу.
, где n-число всех исходов, m-число благоприятствующих исходов.
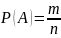
Пр-р: вероятность выпадения решки Р(А)=m/n=1/2
Статистическая вероятность события принимают относительную частоту или число близкое к ней.
Под относительной частотой события понимают отношение m/n, где n-число опытов, m-число появления событий. 
4. Геометрическое определение вероятности. Пример.
Геометрической вероятностью события наз. Отношение меры, благоприятствующей появлению события, к мере всей области.
Пр-р: на плоскости нанесена сетка квадратов со стороной 8 см. найти вероятность, что брошенный на плоскость круг радиуса не пересечет ни одной стороны квадрата.
S(А)=64см 2 , S(В)=36см 2 , Р(А)=36/64=0,6=60%, 
5. Свойства вероятности. Пример.
Вероятность случайного события А, есть положительное число, заключенное между 0 и 1 
Вероятность достоверного события равно 1 
Вероятность невозможного события равно 0 
Сумма вероятностей 2-х противоположных событий равна 1 
6. достоверные, невозможные и случайные события. Пример.
Достоверным событием наз событие, которое обязательно произойдет при определенном комплексе условий (омега)
Пр-р: из ящикас кубиками вытащить кубик – 100%
Невозможное – которое не может произойти в результате данного испытания
Пр-р: из ящика с зелеными кубиками вытащить красный – 0%
Случайное – которое может произойти либо не произойти в результате некоторого события.
7. виды случайных событий. Пример.
Совместные если в результате эксперимента наступление одного из них не исключает появление других. (при бросании монеты появление цифры на одной не иск появление цифр на других.)
Несовместные если появление одного исключает появление других (на экзамене не возможно получить 2 и 3 и 4 и 5)
Единственно возможное если в результате, испытания хотя бы одно из них обязательно произойдет (купил или не купил журнал)
Равновозможные события если в результате испытания ни одно из них не имеет объективно большую возможность появления чем другое (при бросании кости появл каждой грани равновозможное событие)
Противоположные – два единственно возможных и не совместных (попадание и промах при стрельбе)
Полная группа событий — совокупность всех единственно возможных и несовместных событий (получил на экзамене 5,4,3,2)
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
