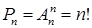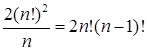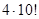Сколькими способами могут сесть 6 человек

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .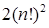

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .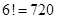

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .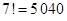

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .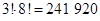

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .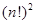

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .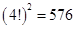

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .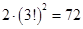

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник

Сколькими способами 6 человек могут сесть на 6 стульев?

Математика | 10 — 11 классы

Сколькими способами 6 человек могут сесть на 6 стульев?

Мне кажется, что ответ будет 6!

N — — кол — во человек, M — кол — во стульев, таким образом :

Остап вошёл в комнату, в которой вокруг круглого стола стояло 12 стульев?

Остап вошёл в комнату, в которой вокруг круглого стола стояло 12 стульев.

Он решил сесть так, чтобы на соседнем с ним стуле никто не сидел.

Присмотревшись Остап увидел, что не сможет этого сделать.

Сколько могло быть занято стульев?

5 мальчиков — Алёша, Коля, Вова, Саша и Дима — хотят сесть на скамейку?

5 мальчиков — Алёша, Коля, Вова, Саша и Дима — хотят сесть на скамейку.

Сколькими способами они могут сделать это?

В классе стояло 9 стульев?

В классе стояло 9 стульев.

Этого оказалось мало, Принесли еще стулья, и все 19 учеников смогли сесть.

Сколько стульев принесли для учеников.

В басне И?

А. Крылова «Квартет» 4 животных никак не могли усесться и начать игру.

Сколькими различными способами могут сесть крыловские музыканты в один ряд?

Сколькими способами можно поставить в ряд 6 стульев ?

Сколькими способами можно поставить в ряд 6 стульев ?

Решите задачу?

Виталик Миша и Сережа пришли вместе сфотографироваться .

Сколькими различными способами они могут сесть.

В Легковой автомобиль могут съесть 4 пассажирп сколько пассажиров могут сесть в три машины?

В Легковой автомобиль могут съесть 4 пассажирп сколько пассажиров могут сесть в три машины.

Виталик Миша и Сергей пришли вместе сфотографироваться ?

Виталик Миша и Сергей пришли вместе сфотографироваться .

Сколькими различными способами они могут сесть.

У круглого стола поставили четыре стула?

У круглого стола поставили четыре стула.

Сколькими способами можно рассадить на эти стулья трёх детей.

Пять мальчиков — Алёша, Коля, Вова, Саша и Дима — хотят сесть на скамейку?

Пять мальчиков — Алёша, Коля, Вова, Саша и Дима — хотят сесть на скамейку.

Скольким способами они могут это сделать?

На этой странице сайта размещен вопрос Сколькими способами 6 человек могут сесть на 6 стульев? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

= — 0, 96b + 3 — 2, 9b + 8 — 16 + 6b = ( — 0, 96b — 2, 9b + 6b) + (3 + 8 — 16) = 2, 14b — 5 приb = — 9 / 13 2, 14 * ( — 9 / 13) — 5 = 214 / 100 * ( — 9 / 13) — 5 = — 1 313 / 650 — 5 = — 6 313 / 650 Пояснение : 214 / 100 * ( — 9 / 13) = — 1926 / 1300 ..

S = π * r² площадь круга S = 3, 14 * 5² = 3, 14 * 25 = 78, 5см² площадь круга 10 * 10 = 100см² площадь квадрата 100 — 78, 5 = 21, 5см² площадь закрашенной части квадрата.

S = 1 × a×h — 2 Нужно просто сосчитать клетки . S = 1×4×10 = 20 см в квадрате — 2.

Икс — 17 = 36 Икс = 36 + 17 Икс = 53.

X — 17 = 36 x = 36 + 17 x = 53 Ответ : 53.

R = 3 (радиус) l = 4 (образующая) Площадь боковой поверхности конуса находится по формуле : S = pi * R * l = 12 * pi.

Решений систем уравнений с помощью матриц. 1)Методом Гаусса 2)Метод Крамера 3)Методом обратной матрицы.

Сложение и умножение : 56 + 78 ; 8 * 7 ; 76 + 6.

18 / 90 = 2 / 10 = 1 / 5 Или 18 / 90 = 9 / 45 = 1 / 5.

Источник

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .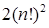

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .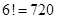

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .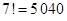

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .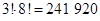

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .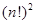

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .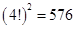

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .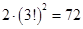

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник