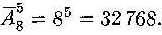Сколькими способами могут быть распределены 3 награды одинаковые между 12 участниками соревнований

Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований помогите пожалуйста?

Алгебра | 10 — 11 классы

Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований помогите пожалуйста.

36 способами так как 3 * 12 = 36.

В соревновании участвуют 10 человек?

В соревновании участвуют 10 человек.

Сколькими способами могут распределиться между ними места?

В конкурсе 8 школьников?

В конкурсе 8 школьников.

Сколькими способами могут быть распределены места между ними?

В соревнованиях по плаванию участвуют 10 спортсменов?

В соревнованиях по плаванию участвуют 10 спортсменов.

Сколькими способами могут быть распределены 1, 2 и 3 места?

Комиссия состоит из главного, его заместителя и ещё 5 человек?

Комиссия состоит из главного, его заместителя и ещё 5 человек.

Сколькими способами члены комиссии могут распределить между собой обязаности главного и заместителя?

В финале международных соревнований по бальным танцам участвуют 6 пар?

В финале международных соревнований по бальным танцам участвуют 6 пар.

Сколькими способами могут распределиться места между ними?

В олимпиаде по математике 32% участников получили грамоты ?

В олимпиаде по математике 32% участников получили грамоты .

Сколько школьников всего приняло участие в олимпиаде , если наградили 416 человек?

В группе 12 ученбных предметов и 4 разных пары в день?

В группе 12 ученбных предметов и 4 разных пары в день.

Сколькими способами могут быть распределены занятия в один день?

Помогите, пожалуйста решить задачу?

Помогите, пожалуйста решить задачу!

На спортивные соревнования прибыло 120 участников , среди которых 36 мастеров спорта и 60 кандидатов в мастера спорта.

А)какую часть от общего числа участников составляют мастера спорта?

, )сколько процентов участников являются кандидатами в мастера спорта?

В) во сколько раз общее число участников больше количества мастеров спорта среди них?

Помогите плизз ?

В финал конкурса вышли шесть его участников .

Сколькими способами могут распределиться два первых места?

В соревновании по настольному теннису было сыграно 66 матчей?

В соревновании по настольному теннису было сыграно 66 матчей.

Определите число участников соревнований, если известно, что каждый участник сыграл с каждым по одному матчу.

Вы открыли страницу вопроса Сколькими способами 3 награды могут быть распределены между 12 участниками соревнований помогите пожалуйста?. Он относится к категории Алгебра. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Алгебра, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Половину нормы, так как интенсивность возросла увеличилась в 6 / 4 = 1, 5 раза.

√(Х — 5)² = 8 Возведём в квадрат обе части (Х — 5)² = 64 Х² — 10х + 25 = 64 Х² — 10х — 39 = 0 Д = √256 = 16 Х1 = (10 + 16) : 2 = 13 Х2 = (10 — 16) : 2 = — 3).

Расстояние = х км (в одну сторону) скорость лодки течению 9 + 3 = 12км \ час значит время тудах / 12часов скорость против течения 9 — 3 = 6км / ч время затратили обратно х / 6 часов. Время в пути 6 — 3 = 3 часа. Составим уравнение : х / 12 + х / 6 ..

Вот) Вроде так Сначала мы применяем формулу разности квадратов, а в след. Скобке раскрываем квадрат) дальше легко решается)).

Источник

Сколькими способами могут быть распределены 3 награды одинаковые между 12 участниками соревнований

Вопрос по алгебре:

сколькими способами 3 награды могут быть распределены между 12 участниками соревнований помогите пожалуйста

Ответы и объяснения 1

36 способами так как 3*12=36

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Источник

Элементы комбинаторики
презентация к уроку по алгебре (9 класс) на тему

В презентации рассмотрены основные понятия комбинаторики, а также приведены решения задач. Данная работа можетбыть полезна на уроках алгебры в 9 классепри изучении темы «Элементы комбинаторики и теории вероятностей», а также на занятиях математического кружка.

Скачать:

Вложение	Размер
elementy_kombinatoriki.ppt	1.07 МБ

Предварительный просмотр:

Подписи к слайдам:

Теорема 1. Правило умножения : если из некоторого конечного множества первый объект (элемент а ) можно выбрать n 1 способами, а второй объект (элемент b ) – n 2 способами, то оба объекта ( а и b ) в указанном порядке можно выбрать n 1 ∙ n 2 способами. Теорема 2. Правило сложения : если некоторый объект а можно выбрать п 1 способами, а объект b можно выбрать n 2 способами, причем первые и вторые способы не пересекаются, то любой из объектов ( а или b ) можно выбрать n 1 + n 2 способами.

Схема выбора без возвращений Размещения из n элементов по k элементов (0 ≤ k ≤ n ) где n ! = 1 ∙ 2 ∙ 3 ∙ … ∙ n, причем 1! = 1, 0! = 1 Перестановки из n элементов Сочетания из n элементов по k элементов (0 ≤ k ≤ n )

Схема выбора с возвращением Размещения с повторениями Сочетания с повторениями Перестановки с повторениями ( n 1 + n 2 + n k = n )

(1-я строка – без повторений, 2-я строка – с повторениями) Размещения Перестановки Сочетания 1 2 ( n 1 + n 2 + n k = n )

Задача 1. Сколько различных трехзначных чисел можно составить из цифр 0, 2, 3, 5, 7 если: а) цифры не повторяются; б) цифры могут повторяться? Решение: а) Первую цифру можно выбрать четырьмя способами (числа вида 025, 073, … не считаем трехзначными). Выбрав первую цифру (например, цифру 5) вторую цифру можно также выбрать четырьмя способами . Третью цифру, очевидно, можно выбрать тремя способами. Следовательно, согласно правилу умножения имеется 4 ∙ 4 ∙ 3 = 48 способов расстановки цифр, т.е. искомых трехзначных чисел будет 48 . б) Если цифры могут повторяться, то трехзначные числа можно составить 4 ∙ 5 ∙ 5 = 100 способами .

Задача 2. Составить различные размещения по два элемента из элементов множества А = <3, 4, 5>и подсчитать их число. Решение: Из трех элементов можно образовать следующие размещения по два элемента: (3,4); (4,3); (3,5); (5,3); (4,5); (5,4). Таким образом, всего их 6. Однако число размещений можно посчитать по формуле: или

Задача 3. Сколькими способами 3 награды (за I , II , III места) могут быть распределены между 10 участниками соревнований? Решение: Будем считать, что каждый участник соревнований может получить не более одной награды. Выбрать 3-х участников из 10 можно следующим образом, так как «призовые тройки» отличаются друг от друга либо составом участников, либо порядком их следования. Этот же результат можно получить, применяя правило умножения: претендентов на главную награду ( I место) 10, на вторую – 9, на третью – 8; число различных способов распределения наград равно 10∙9∙8=720.

Задача 4. В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее: а) 3 гвоздики; б) 6 гвоздик одного цвета; в) 4 красных и 3 розовые гвоздики? Решение: а) Так как порядок выбора цветов не имеет значение, то выбрать 3 гвоздики из вазы, в которой стоят 16 гвоздик, можно б) Выбрать 6 гвоздик красного цвета можно

а 6 гвоздик розового цвета одного цвета (красных или розовых) можно способом. в) Выбрать 4 красных гвоздики из 9 имеющихся можно способами, а 3 розовых из 7 имеющихся можно способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения способами.

Задача 5. На диск сейфа нанесены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова? Решение: Общее число комбинаций можно вычислить по формуле Значит, неудачных попыток может быть 248831. Впрочем, обычно делают сейфы так, что после первой же неудачной попытки открыть их раздается сигнал тревоги.

Задача 6. Пять человек вошли в лифт на 1-м этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах? Решение: Каждый из 5 пассажиров может выйти на любом из восьми этажей со 2-го по 9-ый включительно. Возможными вариантами их выхода являются, например, 2-3-5-5-5 (это значит, что на 2-ом этаже вышел один пассажир, на 3-ем – один, а трое вышли на 5-ом этаже) или 9-9-9-9-9, или 4-5-6-7-9 и т.д. Общее число выходов пассажиров, по формуле равно Этот же результат можно получить, используя правило умножения: для 1-го пассажира имеется 8 вариантов выхода на этаже, для 2-го тоже 8, и для 3-го тоже 8, и для 4-го – 8, и для 5-го – 8. Всего получается 8∙8∙8∙8∙8=8 5 вариантов для выхода 5-ти пассажиров.

Задача 7. Сколько различных « слов » (под « словом » понимается любая комбинация букв) можно составить, переставляя буквы в слове АГА? MISSISSIPPI ? Решение: Из трех букв можно составить Р 3 =3!=6 различных трехбуквенных « слов » . В слове АГА буква А повторяется, а перестановка одинаковых букв не меняет « слова » . Поэтому число перестановок с повторениями меньше числа перестановок без повторений во столько раз, сколько можно переставлять повторяющиеся буквы. В данном слове две буквы (1-ая и 3-я) повторяются; поэтому различных трехбуквенных « слов » из букв АГА можно составить столько: Впрочем, ответ можно получить и проще: каждое слово из букв А, Г и А однозначно определяется положением буквы Г; их всего три, поэтому и различных слов будет тоже три. .

Результат можно получить другой формулой: По этой же формуле найдем число одиннадцатибуквенных « слов » при перестановке букв в слове MISSISSIPPI . Здесь п =11, п 1 =1, п 2 =4 (4 буквы S ), п 3 =4 (4 буквы I ), п 4 =2 (2 буквы Р), поэтому

По теме: методические разработки, презентации и конспекты

Элементы комбинаторики и основы теории вероятности

Данная программа элективного курса объёмом 34 часа рассчитана на учащихся 8 классов и является дополнением общеобразовательной программы, в которой данному вопросу внимания уделяется мало.

Элементы комбинаторики. Поурочные разработки. Алгебра 9 класс

Работа содержит все, что необходимо для подготовки к урокам: подробные поурочные планы, примеры, задачи с разбором решения, разноуровневые проверочные работы.

Элементы комбинаторики. Поурочные разработки. Алгебра 9 класс

Работа содержит все, что необходимо для подготовки к урокам: подробные поурочные планы, примеры, задачи с разбором решения, разноуровневые проверочные работы.

Опорный конспект по теме «Элементы комбинаторики»

В данном конспекте даны основные определения и формулы для вычисления числа перестановок, размещений и сочетаний без повторений. Можно использовать на уроках комбинаторики в 11-м классе (базовый урове.

Тесты по теме «Элементы комбинаторики и теории вероятностей»

В материале предлагается 10 вариантов тестов по теме «Элементы комбинаторики и теории вероятностей». Тесты можно использовать с использованием любого учебника, рекомендованного или допущенного Ф.

«Элементы комбинаторики в школьном курсе математике»

Исторические сведения, дерево возможностей, перестановки, сочетания, размещения.

Методическая разработка «Элементы комбинаторики и теории вероятностей»

Методическая разработка раздела программы по математике.

Источник

Схема выбора с возвращением

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

Во многих задачах классической теории вероятностей используется комбинаторика, т. е. раздел математики, в котором изучаются различные соединения (комбинации) элементов конечных множеств.

Многие комбинаторные задачи могут быть решены с помощью двух правил – правила умножения и правила сложения

Теорема 1. Правило умножения: если из некоторого конечного множества первый объект (элемент а) можно выбрать n₁ способами, а второй объект (элемент b) – n₂способами, то оба объекта (a и b)в указанном порядке можно выбрать n₁ * n₂ способами.

Этот принцип распространяется на случай трех и более объектов.

Теорема 2. Правило сложения: еслинекоторый объект а можно выбрать n₁ способами, а объект b можно выбрать n₂ способами, причем первые и вторые способы не пересекаются, то любой из объектов (а и b) можно выбрать n₁ + n₂ способами.

Это правило распространяется на любое конечное число объектов.

Существуют две схемы выбора элементов из заданного множества: без возвращения, когда выбранные элементы не возвращаются в исходное множество, и с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.

Схема выбора без возвращений

Пусть дано множество, состоящее из n различных элементов.

Размещением из п элементов по k элементов (0

Схема выбора с возвращением

Если при упорядоченной выборке k элементов из п элементы возвращаются обратно, то полученные выборки представляют собой размещения с повторениями. Число всех размещений с повторениями из п элементов по k обозначается символом и вычисляется по формуле

Если при выборке k элементов из п элементы возвращаются обратно без последующего упорядочивания (таким образом, одни и те же элементы могут выниматься по нескольку раз, т. е. повторяться) то полученные выборки есть сочетания с повторениями. Число всех сочетаний с повторениями из п элементов по k обозначается символом и вычисляется по формуле

Пусть в множестве из п элементов есть k различных типов элементов, при
этом 1-й тип элементов повторяется п₁ раз, 2-й – п₂ раз, … k-й – п_k раз, причем п₁ + п₂ + … + п_k = п. Тогда перестановки элементов данного множества представляют собой перестановки с повторениями.

Число перестановок с повторениями (иногда говорит о числе разбиений
множества) из п элементов обозначается символом Рn(п₁ , п₂ , … п_k ) и вычисляется по формуле

Итоговая сводка формул приведена в следующей таблице.

(1- строка — без повторений 2-я строка — с повторениями)

1.1. Сколько различных трехзначных чисел можно составить из
цифр 0, 2, 3, 5, 7если: а) цифры не повторяются; б) цифрымогут повторятся?

О а)Первую цифру можно выбрать четырьмя способами (числа вида
025, 073, .. не считаем трехзначными). Выбрав первую цифру (например, цифру 5),вторую цифру можно также выбрать четырьмя способами (второй цифрой может быть любая из оставшихся 0 2, 3, 7). Третью цифру, очевидно, можно выбрать тремя способами. Следовательно, согласно правилу умножения имеется 4 * 4* 3 = 48 способов расстановки цифр, т е. искомых трехзначных чисел будет 48 (вот некоторые из них: 500, 237, 530, 702, 523, …).

б) Понятно, что если цифры могут повторяться, то трехзначные числа можно составить 4*5*5 = 100 способами (вот некоторые из них: 222, 200, 332, .. ).

1.2. Сколько чисел, содержащих не менее трех попарноразличных цифр можно составить из цифр 2, 4, 6, 8, 9?

ОПо правилу умножения трехзначных чисел можно составить 5*4*3 = 60 способами, а четырехзначных — 5*4*3*2 = 120 способами, столько же пятизначных чисел (5*4*3*2*1). По правилу сложения всего можно составить 60+ 120 + 120 = 300 чисел, состоящих не менее чем из трех попарно различных цифр.

1.3. Сколькими способами могут быть распределены три призовых места среди 16 соревнующихся?

1.4. В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать двух студентов одного пола?

1.5.Если подбросить одновременно три игральные кости то сколько имеется различных возможных комбинаций выброшенных очков?

1.6.В цветочном киоске 7 видов цветов. Сколькими разными способами можно составить букет, содержащий 3 цветка?

1.7.Из пункта А в пункт В можно добраться самолетом, поездом, автобусом а из него в пункт С — пешком, на тракторе, на лошади, на лодке. Сколькимиспособами можно выбрать дорог от пункта А до пункта С через В?

1.8.Сколькимиспособами можно выбрать один цветок из корзины, в которой имеется 12 гвоздик, 15 роз и 7 хризантем?

1.9. Составить различные размещения по два элемента из элементовмножества А (3, 4, 5) и подсчитать их число.

О Из трех элементов можно образовать следующие размещения по два элемента: (3, 4); (4, 3); (3, 5); (5, 3); (4, 5); (5, 4).Таким образом, всех их 6. Однако число размещений можно подсчитать и по формуле (1):

1.10. Сколькими способами 3 награды (за I, II, III места) могут быть
распределены между 10 участниками соревнований?

О Будем считать, что каждый участник соревнований может получить
не более одной награды. Выбрать 3-х участников соревнований из 10 можно

способами, так как призовые тройки отличаются друг от друга либо составом участников, либо порядком их следования.

Этот же результат можно получить, применяя правило умножения: претендентов на главную награду (за 1 место) 9; на вторую — 8; на третью 7; число различных способов распределения наград равно 10*9*8 = 720.

1.11. Сколько имеется пятизначных чисел, все цифры у которых
различны?

1.12. Сколькими способами можно составить трехцветный полосатый флаг (три горизонтальных полосы), если имеется материя 5различных цветов?

1.13. Из группы в 15человек выбирают 4-х участников эстафеты
800 х 400 х 200 х 100. Сколькими способами можно расставить спортсменов на этих этапах?

1.14. Составить различныеперестановки из элементов множества
А <5; 8; 9>.

О По формуле (2)число перестановок из 3-х элементов равно Р₃ = 3! = 1*2*3 = 6, Составляем их: (5, 8, 9); (5, 9, 8); (8, 9, 5); (8, 5, 9); (9, 5, 8);(9, 8, 5).

1.15.Сколькими способами можно расставить на книжной полке десятитомникпроизведений Д. Лондона, располагая их: а) в произвольном порядке; б) так чтобы I, V и IХ тома стояли рядом (в любом порядке); в) так, чтобы I, II, III тома не стояли рядом (в любом порядке).

О а) Число способов расстановки 10 книг равно числу перестановок из
элементов: Р₁₀ = 10! = 3 628 800.

б) Мысленно связав I, V и IХ тома или положив в один пакет, получим 8 книг, т. е, 7 книг и 1 связку (или пакет) книг. Их можно расставить на полке = 8! способами. Каждому из этих способов расстановки соответствуют Рз = 3! способов расстановки книг, находящихся в связке (I, V и IХ тома по-прежнему стоят рядом, но в ином порядке). Согласно правилу умножения, число возможных расстановок 10 книг на полке так, чтобы 3 определенные книги (I, V и IХ тома) стояли рядом равно Р₈ * Р₃ =8! * 3! = 40320 * 6 = 241920.

в) Искомое число способов расстановки книг, с учетом пунктов а) и 5), равно Р₁₀ — Р₈ * P₃ = 3 628 800 — 241 920 = 3 386 880.

1.16. В комнате имеется 7 стульев. Сколькими способами можно разместить па них 7гостей? 3 гостя?

1.17. Студенты дают 5 экзаменов, в том числе 2 экзамена по математике. Сколькими способами можно распределить экзамены но так, чтобыэкзамены по математике следовали один за другим? Не следовали один за другим?

1.18. Сколько различных слов можно получить, переставляя буквы в слове:
а) СОЛНЦЕ; б) ТЕАТР; в) ЛИЛИ; г) SOS?

1.19. Сколькими способами можно упорядочить множество А = <8, 9, 10, 11, . 15>так, чтобы каждое четное число имело четный номер?

1.20. Составить различные сочетания по два из элементов множества А <3, 4, 5>и подсчитать их число

О Из трех элементов можно составить следующие три сочетания по два
элемента: <3, 4>; <3, 5>; <4, 5>.Их число можно подсчитать к по формуле (3):

6.1.21. Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькимиспособами онможет выбрать приглашенных?

ОТак как для Владимира важен только состав гостей (порядок роли не играет), то число способов выбора троих гостей из 7 можно найти по формуле сочетаний (3)

1.22.В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее а) 3 гвоздики; б) б гвоздик одного цвета; в) 4 красных и 3 розовых гвоздики?

О а) Так как порядок выбора цветов не имеет значения то выбрать гвоздики из вазы, в которой стоят 16 гвоздик можно С способами по формуле (3) находим:

б) Выбрать б гвоздик красного цвета можно 84 способами а 6
гвоздик розового цвета = 7 способами. По правилу сложения выбрать б гвоздик одного цвета (красных или розовых) можно = 84 + 7 = 91 способом.

в) Выбрать 4 красных гвоздики из 9 имеющихся можно С способами, а 3 розовых из имеющихся 7 можно С способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения способами

1.23. Сколькими способами можно разбить 8 предметов на две равные (по количеству предметов) группы?

1.24.Группа шахматистов сыграла между собой 28 партий. Каждые два из них встречались между собой один раз. Сколько шахматистов участвовало в соревновании?

1.25.Группа туристов из 12 юношей и 7 девушек выбирает по жребию 5 человек для приготовления ужина. Сколько существует способов, при которых в эту «пятерку» попадут:

а) одни девушки; б) 3 юноши и 2 девушки; в) 1 юноша и 4 девушки; г) 5 юношей?

1.26.Сколькими способами можно разбить 9 предметов на 2 группы (выбор одной группы однозначно определяет вторую)?

1.27.Пять авторов должны написать задачник по математике, состоящий из 14 глав. Два автора напишут по 2 главы два других по 3 и еще один 4 главы книги. Сколькими способами может быть распределен материал между авторами?

1.28.В ящике 15 деталей среди которых 6 бракованных. Наудачу
выбирается комплект из 5 деталей. Сколько всего комплектов, в каждом из которых 2 детали бракованные?

1.29.Из элементов (цифр) 2, 4, 5 составить все размещения и сочетания с повторениями по два элемента,

О Размещения с повторениями по два элемента таковы (2, 2); (2, 4); (2, 5); (4, 4); (4, 5); (4, 2); (5, 5); (5,2); (5,4). Их число можно вычислить и по формуле (4):

Сочетания с повторениями по два элемента таковы (в отличие от размещений здесь порядок элементов в выборке не имеет значения, т е. например пары (2, 4) и (4, 2) не различаются): (2,2); (2, 4); (2, 5); (4, 4); (4, 5); (5, 5).. Их число можно вычислить и по формуле (5):

1.30. В магазине имеется 7 видов тортов. Сколькимиспособами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?

О Поскольку порядок расположения торгов в наборе не играет роли, то искомое число наборов равно числу сочетаний с повторениями из 7 элементов по 3 в каждом. По формуле (5) имеем (см. также задачу 6.1.6).

Если имеется 3 вида тортов, а нужен набор из 7тортов, то число возможных наборов равно

1.31.Пять человек вошли в лифт 1-м этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?

О Каждый из 5 пассажиров может выйтина любом из восьми этажей со 2-го по 9-й включительно. Возможными вариантами их выхода являются, например 2—3—5—5—5 (это значит что на 2-м этаже вышел один пассажир, на 3-м — один, а трое вышли на 5-м этаже) или 9—9—9—9—9 или 4—5—6—7—9, и т.д. Общее число выходовпассажиров, по формуле (4) равно

Этот же результат можно получить, используя правило умножения: для 1-го пассажира имеется 8 вариантов выхода на этаже, для 2-го тоже 8 и для 8-го — 8, и для 4-го – 8 и для 5-го — 8. Всего получается 8*8*8*8*8 = 8 5 вариантов выхода 5-ти пассажиров.

1.32. Сколько различных слов (под «словом» понимается любая комбинация букв) можно составить, переставляя буквы в слове АГА? MISSISSIPPI?

ОВообще из трех букв можно составить Рз = 3! = 6 различных трехбуквенных слов. Вслове АГА буква А повторяется,аперестановка одинаковых букв не меняет «слова». Поэтому число перестановок с повторениями меньше числа перестановок без повторений во столько раз, сколько можно переставлять повторяющиеся буквы. В данном слове две буквы (1-я и 3-я) повторяются; поэтому различных трехбуквенных «слов»

Источник