Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок 1 апельсин
Добрый день, очень требуется помощь в решении следующих задач:
1) В скольких случаях при игре в «Спортлото» (угадывание 5 номеров из 36)будут правильно выбраны не менее3 номеров?
Вариант как я решил: тут используем сочетания C(n,k) = n!/k!(n-k)!. надо просчитать все варианты что бы были выбраны не менее3 номеров, получаем:
С(36,3)- выбор тройки совпавших, С(33,2)- для оставшихся. так же делаем для 4-ёх и 5-ти шаров
С(36,4) — выбор четверки, С(32,1) — оставшиеся
С(36,5) — полное совпадение.
я не понимаю как правильно это всё связать что бы получилось искомые все варианты.
2)Сколькими способами 3 человека могут разделить между собой: 6 одинаковых яблок, 1 апельсин, 1 сливу, 1 лимон, 1 грушу, 1 айву и 1 финик?
Вариант как я начал решить:
Так как яблоки у нас одинаковы то используем явно формулу с повторениями, думал решить через перестановки с повторениями — получилось общие число перестановок:
12!/6!*1!*1!*1!*1!*1!*1!
а вот дальше не понимаю как связать с Размещением, или тут Сочетание?! не могу понять
3) Найти число способов раскладки N различных шаров по M различным корзинам.
Где то видел на форуме уже решение похожей задаче, но если не сложно объясните по действиям как это сделать, точнее логические шаги
4) Вот то что мой мозг окончательно решил отвергнуть:
Чему равен коэффициент при A^10, B^8 в разложении (3+А+B)^20 ?
помогите пожалуйста, и если не составит труда объясните, потому что решаю это для себя и просто необходима помощь знающих людей 
Спасибо.
| | От: | Аноним |
| Дата: | 30.08.11 12:11 | |
| Оценка: |
P>4) Вот то что мой мозг окончательно решил отвергнуть:
P>Чему равен коэффициент при A^10, B^8 в разложении (3+А+B)^20 ?
(3+A+B)^20 = ((A+B) + 3) ^20 = (A+B)^20 + C(20,1)*3*(A+B)^19 + C(20,2)*3^2*(A+B)^18 + (A+B)^17*.. + .
A^10 * B^8 встречается только где-то внутри (A+B)^18. (раскрывая остальные (A+B)^N, получаем что сумма степеней при A и B равна N а значит рассматриваем только N = 18)
Раскрываем (A+B)^18 и ищем коээфициент при A^10 * B^8
Ответ: C(20,2)*9* C(18,10) = 74826180
| | От: | Аноним |
| Дата: | 30.08.11 12:42 | |
| Оценка: |
P>Добрый день, очень требуется помощь в решении следующих задач:
P>1) В скольких случаях при игре в «Спортлото» (угадывание 5 номеров из 36)будут правильно выбраны не менее3 номеров?
У нас есть эталонные выпавшие номера — 5 штук. Необходимо подсчитать сколькими способоми можно выбрать из 36 пятёрки номеров так чтоб совпадало с эталоном не менее 3.
Выбираем 3 номера из эталонных 5, которые будут совпадать. C(5,3). Оставшиеся два номера в нашей пятёрке могут быть любыми, кроме уже выбранных трёх,(любыми — как включая оставшиеся 2 в эталоне — тогда будет более трёх совпадений, так и нет).
Ответ: C(5,3) * С(33, 2)
Комментарий для понимания лотерейной сути: Случай угадывания — это случай когда выбранная пятёрка совпадает с эталонной. Всего вариантов выбора пятёрки («случаев») = C(5,36). Т.е. Вероятность(угадывания не менее 3) = C(5,3) * С(33, 2)/ C(36,5)
| | От: | Кодт |
| Дата: | 02.09.11 10:02 | |
| Оценка: | +1 | |
Здравствуйте, pinosol666, Вы писали:
P>3) Найти число способов раскладки N различных шаров по M различным корзинам.
P>Где то видел на форуме уже решение похожей задаче, но если не сложно объясните по действиям как это сделать, точнее логические шаги
Ну это совсем банально!
Каждой корзине можно сопоставить множество шаров, так, что множества не пересекаются, а их объединение. динамическое программирование, туда-сюда.
НО!
Каждому шару можно сопоставить номер корзины, причём эти номера независимы!
Ergo, раскладка — это N-мерный вектор чисел 1..M. А количество таких векторов — M^N.
| | От: | Буравчик |
| Дата: | 02.09.11 19:54 | |
| Оценка: |
Здравствуйте, pinosol666, Вы писали:
P>1) В скольких случаях при игре в «Спортлото» (угадывание 5 номеров из 36)будут правильно выбраны не менее3 номеров?
P>Вариант как я решил: тут используем сочетания C(n,k) = n!/k!(n-k)!. надо просчитать все варианты что бы были выбраны не менее3 номеров, получаем:
P>С(36,3)- выбор тройки совпавших, С(33,2)- для оставшихся. так же делаем для 4-ёх и 5-ти шаров
P>С(36,4) — выбор четверки, С(32,1) — оставшиеся
P>С(36,5) — полное совпадение.
P>я не понимаю как правильно это всё связать что бы получилось искомые все варианты.
Имеем спортлото 5 из 36 (k из n). То есть 5 выигрышных номеров (k номеров) и 31 невыигрышный (n-k).
Сначала мы хотим угадать ровно 3 номера (m номеров).
— три числа попали в выигрышные => C(5,3) => C(k,m)
— оставшиеся два числа попали в проигрышные => С(31,2) => C(n-k, k-m)
Общее число комбинаций, когда угадано ровно три числа: C(5,3)*С(31,2) => C(k,m)*C(n-k,k-m)
Угаданы не менее 3 номеров, значит угаданы 3, 4, или 5 номеров.
Итоговая вероятность:
[ C(5,3)*С(31,2) + C(5,4)*С(31,1) + C(5,5)*С(31,0) ] / С(36,5)
| | От: | Буравчик |
| Дата: | 03.09.11 20:26 | |
| Оценка: |
Здравствуйте, pinosol666, Вы писали:
P>2)Сколькими способами 3 человека могут разделить между собой: 6 одинаковых яблок, 1 апельсин, 1 сливу, 1 лимон, 1 грушу, 1 айву и 1 финик?
P>Вариант как я начал решить:
P>Так как яблоки у нас одинаковы то используем явно формулу с повторениями, думал решить через перестановки с повторениями — получилось общие число перестановок:
P>12!/6!*1!*1!*1!*1!*1!*1!
P>а вот дальше не понимаю как связать с Размещением, или тут Сочетание?! не могу понять
Раздадим сначала людям яблоки, затем остальные фрукты. Всего каждый человек должен получить по четыре предмета.
Всего яблок шесть. Пусть мы дали каждому по два яблока. Первый человек должен взять два экзотических фрукта (это которые не яблоки). Он может это сделать С(6,2) способами. Второй человек также должен взять два экзотических фрукта. Это С(4,2). Третий забирает все остальное С(2,2). Значит, когда мы дали каждому по два яблока количество вариантов будет равно С(6,2)*С(4,2)*С(2,2).
Рассматриваем все варианты распределения яблок между тремя людьми (разбиения 6 яблок на трех людей). Затем вычислим, сколько экзотических фруктов должен получить каждый человек (оно равно: четыре минус количество полученных яблок). Затем вычислим количество вариантов при каждом распределении яблок.
4+2+0 => 0+2+4 => С(6,0)*С(6,2)*С(4,4)
4+1+1 => 0+3+3 => С(6,0)*С(6,3)*С(3,3)
3+3+0 => 1+1+4 => С(6,1)*С(5,1)*С(4,4)
3+2+1 => 1+2+3 => С(6,1)*С(5,2)*С(3,3)
2+2+2 => 2+2+2 => С(6,2)*С(4,2)*С(2,2)
Суммируем и получаем общее количество вариантов распределения всех фруктов между тремя людьми:
1*15*1 + 1+20*1 + 6*5*1 + 6*10*1 + 15*6*1 = 215 вариантов
Источник
Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок 1 апельсин
Вопрос по математике:
Сколькими способами 3 человека могут разделить между собой 6 одинаковых слив, 1 яблоко, 1 апельсин, 1 киви, 1 банан, 1
грушу и 1 хурму так, чтобы каждый получил по четыре плода?
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Источник
Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок 1 апельсин
Задача 31:
6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?
Решение:
Выложим шары в ряд. Для определения расклада наших шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая – для второго и так далее. Таким образом, число вариантов раскладки шаров по ящикам равно числу способов расположения пяти перегородок. Перегородки могут стоять на любом из 19 мест (между 20 шарами – 19 промежутков). Поэтому число их возможных расположений равно 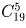
Задача 32:
6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?
Решение:
Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5 одинаковых перегородок, расположенных в произвольном порядке. Каждый такой ряд однозначно соответствует некоторому способу раскладки шаров по ящикам: в первый ящик попадают шары, расположенные левее первой перегородки, во второй – расположенные между первой и второй перегородками и т.д. (между какими-то перегородками шаров может и не быть). Поэтому число способов раскладки шаров по ящикам равно числу различных рядов из 20 шаров и 5 перегородок, т.е. равно 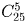
Задача 33:
Сколькими способами натуральное число n можно представить в виде суммы
а) k натуральных слагаемых;
б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?
Решение:
Указание. Представим n в виде суммы n единиц: n = 1 + 1 + … + 1. Назовем теперь эти n единиц «шарами», а k слагаемых из условия задачи – «ящиками». Ответ: а) 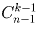
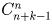
Задача 34:
Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?
Решение:
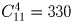
Задача 35:
Переплетчик должен переплести 12 одинаковых книг в красный, зеленый или синий переплеты. Сколькими способами он может это сделать?
Решение:
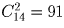
Задача 36:
Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (резать можно только между бусинами)?
Решение:
Нужно указать 8 мест из 30, в которых будут произведены разрезы. Ответ: 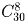
Задача 37:
30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует только за одно предложение и учитывается лишь количество голосов, поданных за каждое предложение?
Решение:
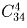
Задача 38:
В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нем
в) 8 различных открыток?
Решение:
а) 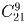
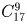
Задача 39:
Поезду, в котором находится m пассажиров, предстоит сделать n остановок.
а) Сколькими способами могут выйти пассажиры на этих остановках?
б) Решите ту же задачу, если учитывается лишь количество пассажиров, вышедших на каждой остановке.
Решение:
а) n m ; б) 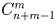
Задача 40:
В кошельке лежит по 20 монет достоинством в 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?
Решение:
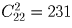
Задача 41:
Сколькими способами можно расположить в 9 лузах 7 белых и 2 черных шара? Часть луз может быть пустой, а лузы считаются различными.
Решение:
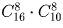
Задача 42:
Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, один апельсин, одну сливу и один мандарин?
Решение:
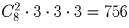
Задача 43:
Сколькими способами 4 черных шара, 4 белых шара и 4 синих шара можно разложить в 6 различных ящиков?
Решение:
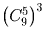
Задача 44:
Общество из n членов выбирает из своего состава одного представителя.
а) Сколькими способами может произойти открытое голосование, если каждый голосует за одного человека (быть может, и за себя)?
б) Решите ту же задачу, если голосование – тайное, т.е. учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально.
Решение:
а) n n ; б) 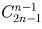
Задача 45:
Сколькими способами можно выложить в ряд 5 красных, 5 синих и 5 зеленых шаров так, чтобы никакие два синих шара не лежали рядом?
Решение:
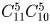
Задача 46:
Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся порядком множителей, считаются различными?
Решение:
1000000 = 2 6 5 6 . Каждый множитель однозначно определяется количеством двоек и пятерок, входящих в его разложение. Суммарное количество в трех множителях как двоек, так и пятерок, равно 6. Ответ: 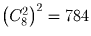
Задача 47:
На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?
Решение:
Рассмотрите 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест однозначно определяет комплект вынутых книг. Ответ: 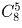
Источник







