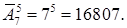Сколькими способами 12 полтинников можно разложить по пяти различным пакетам

Сколькими способами 12 одинаковых монет можно разложить по пяти различным пакетам?

Сколькими способами можно разложить a одинаковых шаров по b различным ящикам?
Сколькими способами можно разложить a одинаковых шаров по b различным ящикам, так, чтобы в каждом.

Сколькими способами можно разложить 7 одинаковых монет в 3 кармана?
С помощью какой формулы надо решать: сочетание, размещение, перестановки?

Сколькими способами можно разложить коллекцию из всех монет?
У девочки есть 15 юбилейных монет 6 монет с изображением Москвы 4 монеты с изображением Сочи.

Сколькими способами можно разложить в 2 кармана 9 чеканных монет
Всем доброго дня!) Есть в учебнике Виленкина в разделе про размещения с повторениями такая задача.

Решение

Сколькими способами 5 монет одного достоинства и 8 другого можно разложить в 4 кармана?
1.Сколькими способами 5 монет одного достоинства и 8 другого можно разложить в 4 кармана? одна.

Сколькими различными способами можно разделить 25 одинаковых монет между четырьмя школьниками?
Сколькими различными способами можно разделить 25 одинаковых монет между четырьмя школьниками? (Два.

Сколькими способами можно разложить 14 одинаковых шаров по 8 ми ящиками?
Сколькими способами можно разложить 14 одинаковых шаров по 8 ми ящиками? Сколько пятизначных.

Сколькими способами можно разложить 28 различных предметов в четыре одинаковых ящика?
Добрый день Нужна ваша помощь Сколькими способами можно разложить 28 различных предметов в.

Сколько способов разложить 12 одинаковых монет по 4 различным карманам
Здравствуйте! Можете помочь решить задачу по комбинаторике? А то я то — то не могу сообразить. .

Сколькими способами можно распределить 10 учебников по двум пакетам
Студент получил 10 учебников. У него есть 2 пакета. Сколькими способами можно распределить их по.

Источник

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

Математика | 10 — 11 классы

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

12умножить на 5 и ответ разделить на пять.

Мама не смогла купить Федору игрушку?

Мама не смогла купить Федору игрушку.

По дороге домой Федор рассуждал : если бы мама положила в свой кошелек еще треть денег находящихся в нем, то в кошельке стало бы 96рб и тогда хватило бы на покупку игрушки.

Сколько денег было у мамы в кошельке?

После того, как мама потратила 1600р?

После того, как мама потратила 1600р.

, она положила в кошелек 400р.

, и в нем стало 3000р.

Сколько рублей было в кошельке сначала?

После того как мама потратила 1 600 р?

После того как мама потратила 1 600 р.

, она положила в кошелек 400 р.

, и в нем стало 3 000 р.

Сколько рублей было в кошельке сначала?

Питерсон 3 класс Математика Коля прочитал вот что : Если к моим деньгам прибавить половинку, то получится 81 рубль?

Питерсон 3 класс Математика Коля прочитал вот что : Если к моим деньгам прибавить половинку, то получится 81 рубль.

Сколько у меня денег?

А Шура прочитала вот что : Если мама положит в кошелек еще треть денег, находящихся в нем то в кошельке станет 68 рублей Сколько денег в кошельке?

(34 Баллов Комбинаторика) Сколькими способами 12 разных монет можно разложить по пяти различным карманам?

(34 Баллов Комбинаторика) Сколькими способами 12 разных монет можно разложить по пяти различным карманам?

Если мама положит в кошелек еще треть денег, находящихся в нем, то в кошельке станет 68 руб?

Если мама положит в кошелек еще треть денег, находящихся в нем, то в кошельке станет 68 руб.

Сколько денег в кошельке.

ЕСЛИ РАЗЛОЖИТЬ МОНЕТЫ ПО 5 В КАЖДЫЙ КОШЕЛЕК, ТО 4 МОНЕТЫ ОКАЖУТСЯ ЛИШНИМИ, А ЕСЛИ РАЗЛОЖИТЬ МОНЕТЫ ПО 6 В КАЖДЫЙ КОШЕЛЕК , ТО 3 — Х МОНЕТ НЕ ХВАТИТ?

ЕСЛИ РАЗЛОЖИТЬ МОНЕТЫ ПО 5 В КАЖДЫЙ КОШЕЛЕК, ТО 4 МОНЕТЫ ОКАЖУТСЯ ЛИШНИМИ, А ЕСЛИ РАЗЛОЖИТЬ МОНЕТЫ ПО 6 В КАЖДЫЙ КОШЕЛЕК , ТО 3 — Х МОНЕТ НЕ ХВАТИТ.

ЗАДАЧУ МЫ РЕШИЛИ, НУЖНО ОБЪЯСНЕНИЕ!

Сколькими способами можно разложить 7 монет по двум карманам так, чтобы ни один карман не был пустым?

Сколькими способами можно разложить 7 монет по двум карманам так, чтобы ни один карман не был пустым?

Если из первого кошелька взять 2 рубля, и положить во второй, то денег в каждом кошельке станет поровну?

Если из первого кошелька взять 2 рубля, и положить во второй, то денег в каждом кошельке станет поровну.

Если же в первый кошелек добавит 8 рублей , а во второй положить столькоже сколько в нем есть , то в каждом кошельке денег опять будет поровну.

Сколько денег в каждом кошельке?

Сколькими способами можно разложить 7 различных писем по семи различным конвертам, если в каждый конверт кладётся только одно письмо?

Сколькими способами можно разложить 7 различных писем по семи различным конвертам, если в каждый конверт кладётся только одно письмо.

Если вам необходимо получить ответ на вопрос Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Источник

Сколькими способами 12 полтинников можно разложить по пяти различным пакетам

Задача 31:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?

Решение:

Выложим шары в ряд. Для определения расклада наших шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая – для второго и так далее. Таким образом, число вариантов раскладки шаров по ящикам равно числу способов расположения пяти перегородок. Перегородки могут стоять на любом из 19 мест (между 20 шарами – 19 промежутков). Поэтому число их возможных расположений равно .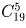

Задача 32:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?

Решение:

Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5 одинаковых перегородок, расположенных в произвольном порядке. Каждый такой ряд однозначно соответствует некоторому способу раскладки шаров по ящикам: в первый ящик попадают шары, расположенные левее первой перегородки, во второй – расположенные между первой и второй перегородками и т.д. (между какими-то перегородками шаров может и не быть). Поэтому число способов раскладки шаров по ящикам равно числу различных рядов из 20 шаров и 5 перегородок, т.е. равно 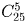(ряд определяется теми пятью местами из 25, на которых стоят перегородки).

Задача 33:

Сколькими способами натуральное число n можно представить в виде суммы

а) k натуральных слагаемых;

б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?

Решение:

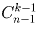
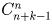
Указание. Представим n в виде суммы n единиц: n = 1 + 1 + … + 1. Назовем теперь эти n единиц «шарами», а k слагаемых из условия задачи – «ящиками». Ответ: а) ; б) .

Задача 34:

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

Решение:

.

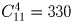
Задача 35:

Переплетчик должен переплести 12 одинаковых книг в красный, зеленый или синий переплеты. Сколькими способами он может это сделать?

Решение:

.

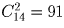
Задача 36:

Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (резать можно только между бусинами)?

Решение:

Нужно указать 8 мест из 30, в которых будут произведены разрезы. Ответ: .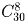

Задача 37:

30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует только за одно предложение и учитывается лишь количество голосов, поданных за каждое предложение?

Решение:

.

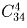
Задача 38:

В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нем

в) 8 различных открыток?

Решение:

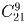
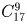
а) ; б) ; в) 10!/2! = 1814400.

Задача 39:

Поезду, в котором находится m пассажиров, предстоит сделать n остановок.

а) Сколькими способами могут выйти пассажиры на этих остановках?

б) Решите ту же задачу, если учитывается лишь количество пассажиров, вышедших на каждой остановке.

Решение:

а) n m ; б) .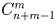

Задача 40:

В кошельке лежит по 20 монет достоинством в 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?

Решение:

.

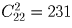
Задача 41:

Сколькими способами можно расположить в 9 лузах 7 белых и 2 черных шара? Часть луз может быть пустой, а лузы считаются различными.

Решение:

.

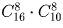
Задача 42:

Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, один апельсин, одну сливу и один мандарин?

Решение:

.

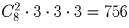
Задача 43:

Сколькими способами 4 черных шара, 4 белых шара и 4 синих шара можно разложить в 6 различных ящиков?

Решение:

.

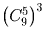
Задача 44:

Общество из n членов выбирает из своего состава одного представителя.

а) Сколькими способами может произойти открытое голосование, если каждый голосует за одного человека (быть может, и за себя)?

б) Решите ту же задачу, если голосование – тайное, т.е. учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально.

Решение:

а) n n ; б) .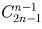

Задача 45:

Сколькими способами можно выложить в ряд 5 красных, 5 синих и 5 зеленых шаров так, чтобы никакие два синих шара не лежали рядом?

Решение:

.

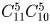
Задача 46:

Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся порядком множителей, считаются различными?

Решение:

1000000 = 2 6 • 5 6 . Каждый множитель однозначно определяется количеством двоек и пятерок, входящих в его разложение. Суммарное количество в трех множителях как двоек, так и пятерок, равно 6. Ответ: .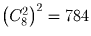

Задача 47:

На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?

Решение:

Рассмотрите 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест однозначно определяет комплект вынутых книг. Ответ: .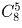

Источник

Сколькими способами 12 полтинников можно разложить по пяти различным пакетам

Пусть имеется три элемента ( n = 3): a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента ( k = 2): ab, ac, ba, bc, ca, cb, aa, bb, cc (порядок важен!)

Общее число размещениями с повторениями определяется формулой:

Пример 1. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?

Решение. Данная задача есть задача на отыскание числа размещений с повторениями

.

Пример 2. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?

Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Пример 3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно .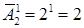

Число всех букв, каждая из которых записывается двумя символами, равно .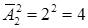

Число всех букв, каждая из которых записывается тремя символами, равно .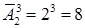

Число всех букв, каждая из которых записывается четырьмя символами, равно .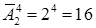

Число всех букв, каждая из которых записывается пятью символами, равно .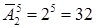

Число всех указанных букв будет равно 62.

Задачи.

1. Сколькими способами можно разложить 12 различных деталей по 3 ящикам?

2. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?

Ответ: .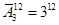

3. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?

Ответ: .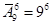

4. Сколькими способами можно разместить 8 пассажиров по трем вагонам?

Ответ: .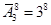

5. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?

Ответ: .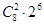

6. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа 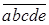(повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a=1; 2) a¹2; 3) a=3, b=2; 4) a=3, b=4, c=5?

Ответ: .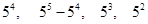

7. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?

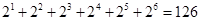
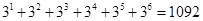
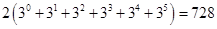
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно . б) Для трёх цифр аналогично получаем . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим чисел.

8. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?

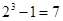
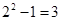
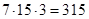
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: способов выбора кур. Точно так же есть способов выбора уток и способов выбора гусей. Всего способов.

Источник