Сколькими способами 12 одинаковых монет можно разложить по пяти разным кошелькам

Содержание

не сложная комбинаторика
Сколькими способами 12 одинаковых монет можно разложить по пяти различным пакетам?
Решение
Сколькими способами 12 одинаковых монет можно разложить по пяти разным кошелькам
Сколькими способами можно разложить 10 одинаковых монет по двум карманам
Решение
Комбинаторика

не сложная комбинаторика

Помогите решить следующую задачку:
Сколькими способами 12 одинаковых монет можно розложить по 5 разных кошелькам так, что бы ни один из кошельков не остался пустым.

И еще одна задачка:
Собрание, на котором присутствуют 30 человек, в том числе 2 женщины, выбирают четырех человек для работы на избирательном участке. Сколько может быть случаев, когда в число избранных войдут обе женщины.

Заранее большое спасибо

Комбинаторика
Помогите пожалуйста!) 9 банкнот достоинством в 1 д.е., 5 — в 10 д.е. наудачу разложили по 3-м.

Комбинаторика.
1) Сколько различных пятизначных чисел, больших за 20000, можно составить из цифр 1,2,3,4, если.

комбинаторика
помогите. не могу решить задачи(( 1. сколько способов разложения семи различных дискет в три.

Комбинаторика
В общем, изучаю комбинаторику в данный момент.Тема «Перестановки». Задание следующее: Hапечатать.

Вторая задачка: C(28, 2) = 28! / (26! * 2!) = 28*27/2
(Женщин можно выбрать единственным способом. Остается выбрать 2-х из 28 мужиков)

Добавлено через 6 минут
Первая. Напрашивается такое решение.
Сначала кладем в каждый кошелек по монете. Остается 7 монет, которые надо разложить по 5 кошелям.
Для любой из монет имеется 5 вариантов, итого 7^5. Но т.к. монеты одинаковы, это надо разделить на 7!
И в ответе — 7^5 / 7! — нецелое!
Что-то тут не так.

Источник

Сколькими способами 12 одинаковых монет можно разложить по пяти различным пакетам?

Сколькими способами можно разложить a одинаковых шаров по b различным ящикам?
Сколькими способами можно разложить a одинаковых шаров по b различным ящикам, так, чтобы в каждом.

Сколькими способами можно разложить 7 одинаковых монет в 3 кармана?
С помощью какой формулы надо решать: сочетание, размещение, перестановки?

Сколькими способами можно разложить коллекцию из всех монет?
У девочки есть 15 юбилейных монет 6 монет с изображением Москвы 4 монеты с изображением Сочи.

Сколькими способами можно разложить в 2 кармана 9 чеканных монет
Всем доброго дня!) Есть в учебнике Виленкина в разделе про размещения с повторениями такая задача.

Решение

Сколькими способами 5 монет одного достоинства и 8 другого можно разложить в 4 кармана?
1.Сколькими способами 5 монет одного достоинства и 8 другого можно разложить в 4 кармана? одна.

Сколькими различными способами можно разделить 25 одинаковых монет между четырьмя школьниками?
Сколькими различными способами можно разделить 25 одинаковых монет между четырьмя школьниками? (Два.

Сколькими способами можно разложить 14 одинаковых шаров по 8 ми ящиками?
Сколькими способами можно разложить 14 одинаковых шаров по 8 ми ящиками? Сколько пятизначных.

Сколькими способами можно разложить 28 различных предметов в четыре одинаковых ящика?
Добрый день Нужна ваша помощь Сколькими способами можно разложить 28 различных предметов в.

Сколько способов разложить 12 одинаковых монет по 4 различным карманам
Здравствуйте! Можете помочь решить задачу по комбинаторике? А то я то — то не могу сообразить. .

Сколькими способами можно распределить 10 учебников по двум пакетам
Студент получил 10 учебников. У него есть 2 пакета. Сколькими способами можно распределить их по.

Источник

Сколькими способами 12 одинаковых монет можно разложить по пяти разным кошелькам

Задача 31:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?

Решение:

Выложим шары в ряд. Для определения расклада наших шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая – для второго и так далее. Таким образом, число вариантов раскладки шаров по ящикам равно числу способов расположения пяти перегородок. Перегородки могут стоять на любом из 19 мест (между 20 шарами – 19 промежутков). Поэтому число их возможных расположений равно .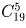

Задача 32:

6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?

Решение:

Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5 одинаковых перегородок, расположенных в произвольном порядке. Каждый такой ряд однозначно соответствует некоторому способу раскладки шаров по ящикам: в первый ящик попадают шары, расположенные левее первой перегородки, во второй – расположенные между первой и второй перегородками и т.д. (между какими-то перегородками шаров может и не быть). Поэтому число способов раскладки шаров по ящикам равно числу различных рядов из 20 шаров и 5 перегородок, т.е. равно 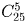(ряд определяется теми пятью местами из 25, на которых стоят перегородки).

Задача 33:

Сколькими способами натуральное число n можно представить в виде суммы

а) k натуральных слагаемых;

б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?

Решение:

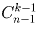
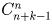
Указание. Представим n в виде суммы n единиц: n = 1 + 1 + … + 1. Назовем теперь эти n единиц «шарами», а k слагаемых из условия задачи – «ящиками». Ответ: а) ; б) .

Задача 34:

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

Решение:

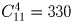
Задача 35:

Переплетчик должен переплести 12 одинаковых книг в красный, зеленый или синий переплеты. Сколькими способами он может это сделать?

Решение:

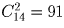
Задача 36:

Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (резать можно только между бусинами)?

Решение:

Нужно указать 8 мест из 30, в которых будут произведены разрезы. Ответ: .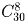

Задача 37:

30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует только за одно предложение и учитывается лишь количество голосов, поданных за каждое предложение?

Решение:

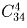
Задача 38:

В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нем

в) 8 различных открыток?

Решение:

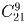
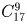
а) ; б) ; в) 10!/2! = 1814400.

Задача 39:

Поезду, в котором находится m пассажиров, предстоит сделать n остановок.

а) Сколькими способами могут выйти пассажиры на этих остановках?

б) Решите ту же задачу, если учитывается лишь количество пассажиров, вышедших на каждой остановке.

Решение:

а) n m ; б) .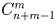

Задача 40:

В кошельке лежит по 20 монет достоинством в 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?

Решение:

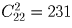
Задача 41:

Сколькими способами можно расположить в 9 лузах 7 белых и 2 черных шара? Часть луз может быть пустой, а лузы считаются различными.

Решение:

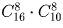
Задача 42:

Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, один апельсин, одну сливу и один мандарин?

Решение:

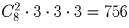
Задача 43:

Сколькими способами 4 черных шара, 4 белых шара и 4 синих шара можно разложить в 6 различных ящиков?

Решение:

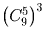
Задача 44:

Общество из n членов выбирает из своего состава одного представителя.

а) Сколькими способами может произойти открытое голосование, если каждый голосует за одного человека (быть может, и за себя)?

б) Решите ту же задачу, если голосование – тайное, т.е. учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально.

Решение:

а) n n ; б) .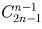

Задача 45:

Сколькими способами можно выложить в ряд 5 красных, 5 синих и 5 зеленых шаров так, чтобы никакие два синих шара не лежали рядом?

Решение:

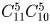
Задача 46:

Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся порядком множителей, считаются различными?

Решение:

1000000 = 2 6 5 6 . Каждый множитель однозначно определяется количеством двоек и пятерок, входящих в его разложение. Суммарное количество в трех множителях как двоек, так и пятерок, равно 6. Ответ: .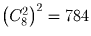

Задача 47:

На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?

Решение:

Рассмотрите 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест однозначно определяет комплект вынутых книг. Ответ: .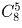

Источник

Сколькими способами можно разложить 10 одинаковых монет по двум карманам

Правильно ли решил?
Сколькими способами можно разложить 10 одинаковых монет по двум карманам?

Сколькими способами 12 одинаковых монет можно разложить по пяти различным пакетам?
Сколькими способами 12 одинаковых монет достоинством в 1р. Можно разложить по пяти различным.

Сколькими способами можно рассовать 10 одинаковых шариковых ручек по 4-м карманам пиджака
Сколькими способами можно рассовать 10 одинаковых шариковых ручек по 4-м карманам пиджака так.

Неверно, хотя хорошо знакомая ситуация!
Falconcheg опередил. Теперь могу отдохнуть!

Добавлено через 6 минут
Хотя Falconcheg тоже ошибся — монеты ведь одинаковые!

Решение

Сколькими способами можно разложить коллекцию из всех монет?
У девочки есть 15 юбилейных монет 6 монет с изображением Москвы 4 монеты с изображением Сочи.

Сколькими способами можно раздать 12 одинаковых монет 7 нищим
Сколькими способами можно раздать 12 одинаковых монет 7 нищим так, чтобы каждый получил не менее.

Источник

Комбинаторика

Логика Перебора. Правило умножения и сложения. Размещения (с повторениями, без повторений). Перестановки (без повторений, с повторениями). Сочетания (без повторений, с повторениями). Формула степени бинома Ньютона, треугольник Паскаля. Решение различных комбинаторных задач.

События и их классификация. Относительная частота событий и ее свойства. Вероятность события и ее свойства. Независимые испытания. Формулы сложения и умножения вероятностей. Условная вероятность. Совместные события. Формула сложения вероятностей. Формула полной вероятности. Формула Байеса. Серия независимых испытаний. Формула Бернулли. Наивероятнейшее число наступлений события.

Таня и Ваня могут сесть рядом 20-ю способами

Размещения (без повторений)

Размещениями из n элементов по R элементов называются подмножества k элементов, отличающихся одно от другого или самими элементами или их порядком.

Ø Сколько трехзначных чисел можно составить из множества цифр 1, 2, 3, 4, 5 без повторений?

Ø Сколькими способами можно распределить два билета в театр между четырьмя людьми? (12 способов).

Ø Сколькими способами можно разложить 7 разных монет в 3 кармана? (210 способов).

Ø Код замка состоит из 4 цифр. Сколько существует способов набора этих цифр, если цифры не повторяются? (5040 способов).

Ø Номер автомашины состоит из 3 цифр. Сколько существует разных номеров, если все цифры разные? (720 номеров). А из четырех цифр? (5040 номеров).

Ø Сколько существует номеров телефона, состоящего из шести различных цифр? (1663200 номеров).

Ø В высшей лиге по футболу 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами они могут быть распределены между командами? (4896 способов).

Размещения с повторениями

v Сколько можно составить различных трехзначных номеров для машин?

v Сколько трехзначных чисел можно составить из цифр 1; 2; 3; 4; 5? (125 чисел).

v Сколько чисел, меньших 105, можно записать с помощью цифр 7; 6; 4?

Числа могут быть однозначные, их три; двузначные, их 32=9; трехзначные 33=27 и т. д.

v Сколько существует пятизначных номеров:

1) не содержащих цифру 8? (59059 номеров).

2) не содержащих 0 и 8? (32768 номеров).

3) составленных из цифр 2; 3; 5; 7? (1024 номера).

v Сколько существует шестизначных номеров телефона? (1000000 номеров).

v Сколько разных четырехзначных чисел можно составить из цифр 0; 1; 2, если цифры могут повторяться?

Всего можно составить: A34=34=81, но числа с нулем впереди не являются четырехзначными, поэтому: A34 – A33=81-27=54

v Сколькими способами можно отослать 6 писем разным адресам, если их будут разносить 3 курьера? (729 способов).

v Четыре студента сдают экзамен. Сколько может быть вариантов распределения оценок, если все они сдали экзамен? (81 вариант).

Перестановки (без повторений)

Перестановками из данных n элементов называются множества из n элементов, различающихся только порядком.

К кассе за получением денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?

Сколько разных пятизначных чисел можно составить из цифр 1; 2; 3; 4; 5? (120 чисел).

Сколькими способами можно расположить на шахматной доске 8 ладей, чтобы они не могли взять друг друга? (40320 способов).

Укротитель хищных зверей хочет вывести на арену цирка 5 львов и 4 тигра, при этом нельзя, чтобы 2 тигра шли друг за другом. Сколько существует способов размещения зверей?

Поставим сначала львов: P5=5!=120. Тигров можно поставить на 6 мест (впереди львов, сзади и между ними): A46=6! : (6-4)!=360. Всего: 120·360=43200 способов.

Сколькими способами можно посадить за круглым столом 5 мальчиков и 5 девочек, чтобы лица одного пола не сидели рядом?

Сначала рассадим девочек: P5=5!. Способов рассадить мальчиков столько же: P5=5! Значит всего (5!)2. Но так как можно рассадить сначала мальчиков, а потом девочек, то всего будет: 2·(5!)2=28800 (способов).

Перестановки с повторениями

Сколько разных слов можно образовать при перестановке букв слова

Сколько слов можно составить при перестановке букв в слове:

1) толпа? (120 слов).

2) топот? (30 слов).

§ Найти сумму четырехзначных чисел, получаемых при возможных перестановках цифр

1) 1; 1; 4; 4; (16665).

§ Мать купила 2 яблока, 3 груши и 4 апельсина. Девять дней подряд она предлагает сыну по 1-ому фрукту. Сколькими способами она может выдавать фрукты? (1260 способов).

Сочетания (без повторений).

Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества называются всевозможные множества, различающиеся хотя бы одним элементом. (Порядок расположения не важен).

На тренировках занимается 12 баскетболистов. Сколько может быть составлено тренером различных стартовых пятерок?

Имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать 3. Сколькими способами можно это сделать? (20 способов).

В ящике 20 шаров, среди которых 12 белых, остальные черные. Отбирается наугад 2 шара. Сколькими способами можно отобрать:

1) 2 белых шара (66 способов);

2) 2 черных шара (28 способов);

3) 1 белый, 1 черный шар? (96 способов).

· Из вазы, в которой стоят 10 красных, 4 розовых и 6 белых гвоздик выбирается 3 красных, 1 розовая и 2 белых. Сколькими способами это можно сделать?

Экипаж корабля состоит из командира, 2-х бортинженеров, врача и 3-х космонавтов. Всего имеются на роль командира 2, на роль бортинженера ─ 3, на роль врача ─ 4, на роль космонавта ─ 5. Сколькими способами можно составить экипаж корабля?

В классе 22 ученика. Надо выбрать командира и 3 звеньевых. Сколькими способами это можно сделать? (7315 способов).

Сколько разных стартовых шестерок можно образовать из 10 волейболистов? (210).

Для полета на Марс необходимо укомплектовать следующий экипаж корабля: командир, 1-ый помощник, 2-ой помощник, 2 бортинженера и 1 врач. Можно отобрать из 25 летчиков, 20 специалистов и 8 медиков. Сколькими способами можно укомплектовать экипаж корабля?

При выборе командира и его помощников важно определить, какой из летчиков лучше справляется с теми или иными функциями, поэтому: A253=25·24·23=13800

C202=190 (способов выбора бортинженеров)

C81=8 (способов выбора врача)

A253·C202·C81·=20 976 000

Сочетания с повторениями

Объем выборки k, а множество, из которого строятся выборки, содержит n элементов.

ü В гастрономе имеются конфеты в коробках 3-х сортов. Сколькими способами можно заказать 5 коробок?

ü В продажу поступили открытки 10 разных видов. Сколькими способами можно отобрать 12 открыток? (293 930 способов).

ü Сколько существует различных треугольников, длины сторон которых принимают значения 8; 10; 12 и 14 см? Сколько среди них равнобедренных, равносторонних?

C43=20 ─ всего треугольников

ü Сколько существует различных треугольников, длины сторон которых принимают значения 5; 6; 7; 8; 9? (35 треугольников).

ü Сколько наборов из 7 пирожных можно составить, если в продаже 4 сорта? (120 наборов).

Элементы теории вероятностей

1) События и их классификация.

События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании. В противном случае события называются совместными.

Несовместность более чем двух испытаний означает их попарную несовместность.

Событие называется невозможным, если при испытании оно не может произойти.

Случайным называется событие, которое может либо произойти, либо не произойти.

События называются равновозможными, если ни одно из них не является более возможным, чем другое.

Два единственно возможных события, образующих полную группу, называются противоположными.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

Событие называется достоверным, если оно обязательно произойдет при данном испытании.

При одном выстреле по мишени возможны следующие события:

а) А ─ попадание в цель;

А и В ─ противоположные, несовместные, случайные.

Камень подбрасывается вверх.

а) А ─ камень упадет на землю;

б) В ─ камень улетит в космос.

А ─ достоверное; В ─ невозможное.

Из партии посевного зерна отбираются 2 зерна.

а) А ─ 1-ое зерно взойдет;

б) В ─ 2-ое зерно взойдет.

А и В ─ случайные, совместные.

а) А ─ выпадает «орел»;

б) В ─ выпадет «цифра».

А и В ─ случайные, противоположные, несовместные, равновозможные.

Какими являются следующие события?

а) У человека есть сердце.

б) После воскресенья наступит вторник.

в) В феврале 28 дней.

г) У человека есть родители.

д) У человека есть дети.

е) Город находится в России.

ж) Число ─ четное.

з) Река впадает в Каспийское море.

и) Земля вращается вокруг Солнца.

к) Утром светит солнце.

л) Ночью идет дождь.

м) Летом цветут цветы.

н) Ученик получил оценку «5».

о) Человек умеет плавать.

п) Квадрат не имеет углов.

р) Круг желтого цвета.

с) Птицы имеют крылья.

Суммой А+В двух событий А и В называются события, состоящие в появлении события А или события В, или обоих этих событий.

Произведены 2 выстрела.

А ─ попадание при первом выстреле;

А+В ─ стрелок попал (один или два раза).

Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий.

Произведением А · В называется событие, состоящее в совместном появлении этих событий.

А · В ─ попал и 1, и 2 раз.

Относительная частота событий и ее свойства

Относительной частотой (частостью) события называется число

m ─ число появлений события А;

n ─ общее число проведенных испытаний.

Стрелок сделал 1000 выстрелов по мишеням и попал 90 раз.

Источник