Сколькими разными способами можно распределить между шестью лицами две разные путевки

Элементы комбинаторики.

Одно из важнейших правил комбинаторики – правило произведения.

Правило произведения. Если объект A₁ может быть выбран k₁ способами, затем для каждого из таких выборов объекта A₁ другой объект A₂ может быть выбран k₂ способами, затем для каждого из таких выборов и объекта A₁, и объекта A₂ третий объект A₃ может быть выбран k₃ способами и т.д., наконец, объект A_m может быть выбран k_m способами, тогда объект «A₁ и A₂, и A₃, и …, и A_m» может быть выбран способами.

Сочетаниями из n различных элементов по m элементов (m≤n)называют комбинации из m элементов, которые составлены из данных n элементов и отличаются хотя бы одним элементом. Число сочетаний из n элементов по m обозначают или и вычисляют по формуле: , где n! (читают «эн факториал») – произведение натуральных чисел от 1 до n: , причем 0!=1.

Пример 1. Сколькими способами между тремя сотрудниками можно распределить две различные путевки?

Решение. Претендент на первую путевку – один из трех сотрудников – может быть выбран тремя способами. Если первая путевка досталась первому сотруднику, то вторая может достаться или второму, или третьему сотруднику. Если первая путевка досталась второму сотруднику, то вторая может достаться или первому, или третьему сотруднику. Если первая путевка досталась третьему сотруднику, то вторая может достаться или первому, или второму сотруднику. Таким образом, для каждого способа распределения первой путевки претендент на вторую путевку может быть выбран двумя способами. Две различные путевки (и первая, и вторая) по правилу произведения могут быть распределены шестью способами:

1) первому и второму сотрудникам;

2) первому и третьему сотрудникам;

3) второму и первому сотрудникам;

4) второму и третьему сотрудникам;

5) третьему и первому сотрудникам;

6) третьему и второму сотрудникам.

Ответ: шестью способами.

Пример 2. Сколькими способами между тремя сотрудниками можно распределить две одинаковые путевки?

Решение. Искомое число равно числу способов выбора из трех сотрудников двух претендентов на путевки. Поскольку 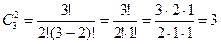, то распределить две одинаковые путевки между тремя сотрудниками можно тремя способами.

Ответ: тремя способами.

7.1.1. Сколькими способами можно составить флаг, содержащий три горизонтальные полосы различных цветов, если имеется материал пяти цветов? Ответ: 60.

7.1.2. Сколькими способами из группы студентов в двадцать пять человек можно выбрать старосту и физорга? Ответ: 600.

7.1.3. Десять спортсменов разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами? Ответ: 720.

7.1.4. Студентам нужно сдать четыре экзамена за восемь дней. Сколькими способами можно составить расписание сдачи экзаменов? Ответ: 1680.

7.1.5. Сколько словарей нужно издать, чтобы непосредственно выполнить переводы с любого из трех языков: русского, английского, французского — на любой другой из этих трех языков? Ответ: 6.

7.1.6. Сколькими способами можно рассадить на скамейке трех человек? Ответ: 6.

7.1.7. Сколькими способами пять книг разных авторов можно расставить на полке? Ответ: 120.

7.1.8. В конкурсе по пяти номинациям участвуют десять кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены различные призы? одинаковые призы? Ответ: 30240; 252.

7.1.9. В хоккейном турнире участвуют шесть команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире? Ответ: 15.

7.1.10. Сколькими способами читатель может выбрать три книжки из пяти имеющихся различных книг? Ответ: 10.

7.1.11. Сколькими способами можно в строчку написать три плюса и два минуса? Ответ: 10.

7.1.12. В лабораторной клетке содержат пять белых и пять коричневых мышей. Найдите число способов выбора: а) трех мышей, если они могут быть любого цвета; б) трех белых мышей. Ответ: 120; 10.

7.1.13. В ящике двадцать кубиков, среди которых пятнадцать окрашены. Сколькими способами можно взять пять кубиков? пять окрашенных кубиков? Ответ: 15504; 3003.

Источник

комбинаторика

Презентация предназначена в помощь ученикам, пропустившим занатия в школе для самостоятельного изучения темы.

Скачать:

Вложение	Размер
kombinatorika.ppt	2.53 МБ

Предварительный просмотр:

Подписи к слайдам:

Комбинаторика Перестановки Размещения Сочетания Презентация выполнена Учеником 10 «а» класса Окуневым Никитой.

Произведения n натуральных чисел от 1 до n обозначается n! ( n факториал ) 1 * 2 * 3 * … * ( n – 1)*n =n! Например: 1*2*3=3! 1*2*3*4*5*6*7*8=8 ! Перестановки Условились считать что: 1!=1 0!=1 Перестановка из n элементов – это расположение их в определённом порядке Например: составим перестановку из х1 х2 х3 х1 х2 х3 х2 х1 х3 х3 х1 х2 х1 х3 х3 х2 х3 х1 х3 х2 х1 Таким образом получаем шесть перестановок

Для любого натурального числа n справедлива формула P n = n! Где P – количество перестановок, а n – число элементов

Задания Вычислите: 7! 5! Ответ: 42

Как – то раз в воскресенье семеро друзей зашли в кафе, уселись за один столик и заказали мороженное. Хозяин кафе сказал, что если друзья в каждое следующее воскресенье будут садиться по новому и перепробуют все способы посадки, то с этого момента он будет кормить их мороженным бесплатно. Удастся ли друзьям воспользоваться предложение ? Ответ: Нет, потому что им нужно будет приходить в кафе 5040 недель 7!=5040

Размещения Размещением из n элементов по k называют любой упорядоченный набор из k элементов , составленный из данных n элементов. Например: составим размещения х1 х2 х3 по 2 х1 х2 х1 х3 х2 х3 х2 х3 х3 х1 х3 х2 Таким образом получилось 9 размещений

n! (n — k)! k A n = n (n — 1)(n — 2)*…*(n – k + 1) A n k Где n – число элементов , а k – число размещений Например: выпишите все размещения из четырёх элементов по два – А 2 4 =4(4 — 1)=4*3=12 А 2 4 = 4 !/ (4 — 2)! = 24/2=12

Задания Вычислите А 7 Ответ: 2520 5 7! (7-5)! 3*4*5*6*7=2520

Сколькими различными способами можно распределить между шестью лицами четыре разные путёвки в санаторий Ответ: 360 6! 2 = 360

Сочетания Сочетанием из данных n элементов по k называют любую группу из k этих элементов Например: из трёх элементов х1 х2 х3 можно составить следующие сочетания по два элемента: х1 х2 х1 х3 х2 х3 Других сочетаний из рассматриваемых элементов по два нет

С n k n! k!(n — k)! Где n – число элементов , а k – число c очетаний Например: Выпишите все сочетания из пяти элементов по два С= 5!/2!(5 — 2)!=120/12=10

Задания Вычислите С 7 5 7! 5!(7-5)! 42 2 24 Ответ:24

Источник

Дополнения к главе IV (4 часа). Размещением из n элементов по два называют любую упорядоченную пару, составленную из данных n элементов. Количество размещений. — презентация

Презентация была опубликована 9 лет назад пользователемschool6.ucoz.com

Похожие презентации

Презентация на тему: » Дополнения к главе IV (4 часа). Размещением из n элементов по два называют любую упорядоченную пару, составленную из данных n элементов. Количество размещений.» — Транскрипт:

1 Дополнения к главе IV (4 часа)

2 Размещением из n элементов по два называют любую упорядоченную пару, составленную из данных n элементов. Количество размещений из n элементов по два обозначают через (по первой букве французского слова arrangement – размещение)

3 a, b, с Ниже написаны все размещения из 3 элементов a, b, с по 2: abac babc cacb

4 Сколькими способами можно распределить два билета на разные кинофильмы между семью друзьями? Размещением из n элементов по k называют любой упорядоченный набор из k элементов, составленный из данных n элементов.

10 Сочетанием из n элементов по k называют любую группу из k элементов, составленную из данных n элементов. Число сочетаний из n элементов по k обозначают через (по первой букве французского слова combination – сочетание). Разница заключается в том, что если в размещении переставить местами элементы, то получится другое размещение, но сочетание не зависит от порядка входящих в него элементов. Разница заключается в том, что если в размещении переставить местами элементы, то получится другое размещение, но сочетание не зависит от порядка входящих в него элементов.

20 Сколькими различными способами можно распределить между шестью лицами две разные путевки в санатории?

21 Сколькими способами можно распределить две одинаковые путевки между пятью лицами?

22 Сколькими способами можно присудить шести лицам три одинаковые премии?

24 Иванов и Степанов входят в группу из семи студентов, имеющих одинаковые шансы получить один из двух разных призов. Какова вероятность того, что: a) Иванов получит первый приз, а Степанов – второй; b) Иванов и Степанов получат призы; c) Иванов получит первый приз; d) Иванов получит один из призов?

25 Из перетасованной колоды, состоящей из 36 карт, наугад взяты 4 карты. Какова вероятность того, в эту четверку: попадут тузы бубен, пик, червей и треф в указанном порядке; попадут 4 туза (в любом порядке); попадет туз бубен и его возьмут первым; попадет туз бубен?

Источник

Описательная статистика (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10

Для п = 1 формула верна по определению. Для п = 2, 3 она уже проверена нами. Чтобы проверить её для n = 4, рассуждаем так. Составим четыре ряда перестановок для цифр 1, 2, 3, 4. В первый ряд поставим все перестановки, начинающиеся с 1:

1234, 1243, 1324, 1342, 1423, 1432.

Таких перестановок 6 = 3!, т. е. столько, сколько раз можно переставить три цифры 2, 3, 4, стоящие после цифры 1.

Но на первое место можно поставить любую из четырёх цифр, и в каждом таком случае получится 6 перестановок, т. е. всего перестановок

Р4 = 4 × Р3 = 4 × 3! = 4!

Доказать, что Рп = п! для любого натурального числа п можно с помощью метода математической индукции.

752. Что называют перестановкой из п элементов?

753. Что обозначает и как читается запись: а) 2!; б) 3!; в) 6!; г) п! ?

754. Выпишите все перестановки из цифр 1, 2, 3. Чему равно P3?

755. Выпишите все возможные перестановки из четырёх букв и подсчитайте их количество (P4).

756. Проказница-Мартышка, Осёл, Козёл да Косолапый Мишка затеяли сыграть квартет. Выясните, сколькими способами они могут сесть со своими инструментами на четыре места.

758 Верно ли, что:

760. У кассира автобуса имеются для продажи билеты на автобус с номерами от 000000 до 999999. Сколько номеров билетов из этого набора записаны цифрами 1, 2, 3, 4, 5, 6 без повторения?

Размещением из п элементов х1, х2, х3, . , хп по два называют любую упорядоченную пару, составленную из данных п элементов. Количество размещений из п элементов по два обозначают через (размещение по-французски arangement).

Ниже выписаны все размещения из 3 элементов по 2:

В первом ряду на первом месте стоит элемент х1, к нему приписаны поочерёдно остальные два элемента. Получилось, что в первом ряду находятся все размещения, начинающиеся с х1, — их два. Во втором и в третьем рядах находятся тоже по два размещения, начинающихся с х2 и с х3. Таким образом, =3 × 2.

Размещения из п элементов по два можно расположить в п рядов. В каждом из них на первом месте стоит один из данных элементов хi, к нему поочерёдно приписываются остальные п – 1 элементов. Этим мы доказали формулу

= n(n – 1). (1)

Пример. Сколькими способами можно распределить два билета на разные кинофильмы между семью друзьями?

Число способов, с помощью которых можно распределить два билета на разные кинофильмы между семью друзьями, равно = 7 × (7 – 1) = 42.

Чтобы в этом убедиться, выпишем все возможные размещения в виде двузначных чисел, первая цифра которых показывает, какому другу достался первый билет, вторая — какому второй:

12, 13, 14, 15, 16, 17,

21, 23, 24, 25, 26, 27,

71, 72, 73, 74, 75, 76.

В каждом из семи рядов по 6 размещений — всего 7 × 6 = 42 размещения, т. е. число способов распределения двух билетов в данной задаче равно 42.

Размещением из п элементов по k называют любой упорядоченный набор из k элементов, составленный из данных п элементов.

Количество размещений из п элементов по k обозначают через . Например, находим следующим образом. Расположим размещения в п рядов. В i-м ряду поместим размещения, начинающиеся с элемента хi. После элемента хi поставим все возможные размещения из оставшихся п – 1 элементов по 2, т. е. (п – 1)(n – 2) различных размещений. Но всего строк п, поэтому = п(п – 1)(п – 2).

Рассуждая подобным же образом, получим, что

= п(п – 1)(п – 2)(п – 3).

Источник