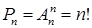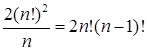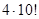Сколькими различными способами можно посадить за стол

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .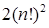

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .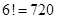

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .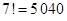

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .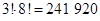

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .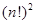

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .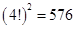

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .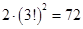

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?

Здравствуйте, уважаемые. Я к вам снова по поводу комбинаторики. Есть задача:
Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? А если они садятся не за круглый стол, а на карусель (способы, переходящие друг в друга при вращении карусели, считаются совпадающими) ?

Первая часть задачи решается как n!*n!, а как решить про карусель, я не поняла? Спасибо большое!

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.

Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две женщины не сидели рядом?
Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две.

Сколькими способами можно посадить n мужчин и n женщин за круглый стол с определенным условием?
Сколькими способами можно посадить n мужчин и n женщин за круглый стол так, чтобы никакие два лица.

Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.

kristi1, разделите на 2n

Добавлено через 3 минуты
Кстати, первая часть — 2*n!*n!, т.к. на стул номер 1 можно посадить как мужчину, так и женщину

Решение

стол от карусели отличается тем, что стулья за столом пронумерованы: есть стул №1, стул №2. стул №10
на карусели нумерация отсутствует

за столом
сначала, как и положено, усаживаем женщин так, чтобы между ними были пустые места
это можно сделать 5! = 120 способами (число перестановок)
однако усадить женщин можно как начиная со стула №1 (по нечётным местам), так и со стула №2 (по чётным местам)
следовательно, 5 женщин можно рассадить 2 * 120 = 240 способами

на оставшиеся 5 мест сядут мужчины — 5! = 120 способами

в итоге за стол мужчин и женщин можно посадить 240 * 120 = 28 800 способами
или в общем виде для n пар мужчин и женщин за столом — 2*n!*n!

на карусели нет нумерации, следовательно, коэффициент 2, введёный при рассадке женщин, не нужен
ответ для карусели — 14 400 способов
в общем виде для n пар мужчин и женщин на карусели — n! * n!

в решении выше ошибка — умножается на 2 (для стола) правильно, а делится (для карусели) почему-то на 2n, что неправильно

Источник

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом? — Комбинаторика — Ответ 3435117

Ответ

стол от карусели отличается тем, что стулья за столом пронумерованы: есть стул №1, стул №2. стул №10
на карусели нумерация отсутствует

за столом
сначала, как и положено, усаживаем женщин так, чтобы между ними были пустые места
это можно сделать 5! = 120 способами (число перестановок)
однако усадить женщин можно как начиная со стула №1 (по нечётным местам), так и со стула №2 (по чётным местам)
следовательно, 5 женщин можно рассадить 2 * 120 = 240 способами

на оставшиеся 5 мест сядут мужчины — 5! = 120 способами

в итоге за стол мужчин и женщин можно посадить 240 * 120 = 28 800 способами
или в общем виде для n пар мужчин и женщин за столом — 2*n!*n!

на карусели нет нумерации, следовательно, коэффициент 2, введёный при рассадке женщин, не нужен
ответ для карусели — 14 400 способов
в общем виде для n пар мужчин и женщин на карусели — n! * n!

в решении выше ошибка — умножается на 2 (для стола) правильно, а делится (для карусели) почему-то на 2n, что неправильно

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, не подскажите как сделать подобную задачу если надо рассадить на карусель 6 детей и 3.

Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две женщины не сидели рядом?
Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две.

Сколькими способами можно посадить n мужчин и n женщин за круглый стол с определенным условием?
Сколькими способами можно посадить n мужчин и n женщин за круглый стол так, чтобы никакие два лица.

Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.

Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.

Сколькими способами можно выбрать 4 женщин и 3 мужчин?
Сколькими способами можно выбрать 4 женщин и 3 мужчин из 9 женщин и 6 мужчин, если не могут быть.

Сколькими способами можно составить компанию из 6 мужчин и 6 женщин?
3)У мужа 12 знакомых, среди которых 5 женщин и 7 мужчин, а у жены 7 женщин и 5 мужчин. Сколькими.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Источник

Рассадка гостей

Добрый вечер! У меня есть задача:

Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколькими различными способами можно посадить четырех человек? А семь человек? Во скольких случаях два данных человека из семи оказываются соседями? Во скольких случаях данный человек (из семи) имеет двух данных соседей?

Мой вариант решения для 4-х гостей: 4*3*2*1 Это же неправильно? Расскажите пожалуйста как это делать? Спасибо!

Добавлено через 16 часов 37 минут
Никто не подскажет?((

Перебор вариантов приглашения гостей на день рождения
Добрый день Прошу помочь в решении. День бьюсь, не могу понять пока решения. Задача следующая.

Распределение (рассадка) сотрудников по рабочим местам
Приветствую всех гением, спасите мой мозг! Не давно столкнулся с такой проблемой: Есть excel файл с.

Задача про гостей
Задача: представьте, что вы намерены пригласить к себе шестерых гостей, но за вашим столом могут.

Скрипт IP гостей сайта
Подскажите что в index.php дописать что бы в текстовый документ записывались ip гостей сайта и.

Решение

гостей всего — m
соседей у одного гостя — n (всегда равно 2)
разных пар двух соседей для одного гостя — число сочетаний из (m — 1) по n

и для n = 2 окончательно

решения:
для 4-х гостей:

в формуле не учитывается «сторона соседства» — «слева Маша, справа Даша» и «слева Даша, справа Маша» считаются одним вариантом.
очевидно, что количество способов рассадки при учёте «сторон соседства» будет вдвое большим.

kristi1, Возьмем рассадку A. В нее приходит человек и создает n новых рассадок, пусть это будет множество R_A. Все они разные с точки зрения соседства.
Теперь возьмем другую рассадку B (она отличается от A). Снова приходит этот тип и создает множество R_B. Но не факт, что множества R_A и R_B не пересекаются, т.е. что нет одинаковых с точки зрения соседства. Т.е. я просто не знаю, как это доказывать.
Плюс, мои результаты не совпадают с результатами Notortep, что наводит на мысль, что скорее всего я ошибаюсь

Добавлено через 43 минуты
Чтобы проверить свои предположения, обратился к эксперементу. Написал программку перебора.
Вот результат
F(3) = 1
F(4) = 3
F(5) = 12
F(6) = 60
F(7) = 360
F(8) = 2520
Выходит, моя формула правильная!
Правда и программа может содержать ошибки, но она такая простенькая!
Плюс совпадение для n=3, n=4 утешают.

Добавлено через 4 минуты
Кажется, можно доказать, что если какие-то рассадки из R_A и R_B совпадают, то совпадают и A с B

Источник

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?

Сколькими способами можно посадить за стол мужчин и женщин так, чтобы два лица одного пола не сидели рядом?
Здравствуйте, уважаемые. Я к вам снова по поводу комбинаторики. Есть задача: Сколькими.

Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две женщины не сидели рядом?
Сколькими способами мужчин и женщин можно усадить за круглый стол так, чтобы никакие две.

Сколькими способами можно посадить n мужчин и n женщин за круглый стол с определенным условием?
Сколькими способами можно посадить n мужчин и n женщин за круглый стол так, чтобы никакие два лица.

Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12 мужчин и 20 женщин?
Сколькими способами можно выбрать комитет,включающий 6 мужчин и 8 женщин из группы, состоящий из 12.

Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.

Сколькими способами можно их рассадить за 10 партами, так чтобы за одной партой не сидели 2 девочки
В классе 12 мальчиков и 8 девочек. Сколькими способами можно их рассадить за 10 партами, так чтобы.

Сколькими способами можно выбрать 4 женщин и 3 мужчин?
Сколькими способами можно выбрать 4 женщин и 3 мужчин из 9 женщин и 6 мужчин, если не могут быть.

Сколькими способами можно составить компанию из 6 мужчин и 6 женщин?
3)У мужа 12 знакомых, среди которых 5 женщин и 7 мужчин, а у жены 7 женщин и 5 мужчин. Сколькими.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Сколькими способами можно посадить рядом 3 англичанина, 3 француза и 3 турка?
Сколькими способами можно посадить рядом 3 англичанина, 3 француза и 3 турка так, что никакие три.

Источник