Сколькими различными способами можно переставить эти буквы

13. Перестановки с повторениями

При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет . Мы имеем здесь дело с перестановками с повторениями.

Общую задачу сформулируем следующим образом.

Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, . Сколько можно составить различных перестановок из этих элементов?

Число перестановок c повторениями обозначают . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом способами так, что она остаётся неизменной.

Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

, (11.1) где .

Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:

.

Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?

Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем

.

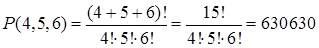
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?

Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:

.

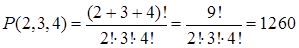
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем

.

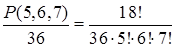
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?

Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим

.

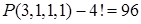
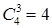
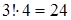
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем способа.

11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?

Ответ: .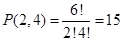

11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?

Ответ: .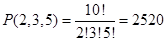

11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?

Ответ: .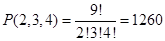

11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?

Ответ: .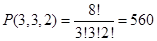

11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?

Ответ: .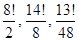

11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?

Ответ: .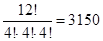

11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?

Ответ: .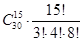

11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?

Ответ: .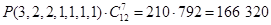

11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?

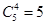
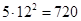
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего способов.

Источник

Перестановка букв в слове, чтоб буквы не стояли рядом

Прошу,помогите

Задача такая: Сколько разных слов можно получить, переставляя буквы слова «КОНДЕНСОВАНIСТЬ» ,если буквы Н не должны стоять рядом?
Начала решать:
1)Нашла число всех возможных перестановок N, учитывая, что буква «Н» в слове повторяется три раза:
N= 15!/3! = 217945728000
2)Потом нашла число К в которых три буквы «Н» стоят рядом(считала их как одну букву)
К= 13!= 6227020800
3)А потом получила число способов перестановок букв в слове так, чтобы три буквы «Н» не стояли рядом
N-K =217945728000-6227020800=211718707200

Но такого быть не может! Как я понимаю,тут дело в мягком знаке, который не может стоять в начале слова.Но как посчитать так,чтобы это учитывалось?

Перестановка букв в слове
Пополню список бездарей, которые не понимают эти задачи, здесь уже был мой пример с просьбой от.

Перестановка букв в слове
Сколько различных слов можно получить перестановкой букв слова А, где А — «диктатура» и условие для.

Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не.

Сколькими способами можно переставить буквы в слове «пурпур», чтобы одинаковые буквы не были рядом
Вот такая задачка попалась. Сколькими способами можно переставить буквы в слове «пурпур»,чтобы.

Источник

Решения задач по комбинаторике

Решения задач по комбинаторике

I. На использование принципов умножения и сложения

1. Сколькими способами могут восемь человек стать в очередь к театральной кассе?

Существует 8 мест, которые должны занять 8 человек. На первое место может стать любой из 8 человек, т. е. способов занять первое место – 8. После того, как один человек стал на первое место, осталось 7 мест и 7 человек, которые могут быть на них размещены, т. е. способов занять второе место – семь. Аналогично для третьего, четвертого и т. д. места. Используя принцип умножения, получаем произведение – . Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8.

2. Позывные радиостанции должны начинаться с буквы W. 1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из трех букв, причем эти буквы могут повторяться? 2) Если позывные состоят из четырех букв, которые не повторяются?

В современном латинском алфавите 26 букв. На первом месте всегда должна стоять одна буква, следовательно, существует только один способ занять первое место.

1) На оставшиеся два места может претендовать любая из 26-ти букв, т. к. буквы в позывных могут повторяться. Используя принцип умножения, получаем произведение: 1= 262.

2) На второе место можно поставить любую из 25 букв, т. к. в позывных буквы не должны повторяться. На третье место – 24 буквы, на четвертое место – 23 буквы. Используя принцип умножения, получаем произведение: 1.

Ответ:; 2) .

3. В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?

Действие, которое должно быть выполнено особым способом, необходимо выполнять первым. Итак, на место водителя можно посадить только одного из трех человек (умеющего водить машину), т. е. существуют 3 способа занять первое место. Второе место может занять любой из 6 человек, оставшихся после того, как место водителя будет занято. И т. д. Используя принцип умножения, получаем произведение: 3 = 36! = 3P6.

Ответ: 3P6 = 36!.

4. Алфавит некоторого языка содержит 30 букв. Сколько существует шестибуквенных слов (цепочка букв от пробела до пробела), составленных из букв этого алфавита, если:

1) буквы в словах не повторяются?

2) буквы в словах могут повторяться?

Существует шесть мест, на которые нужно разместить 30 букв.

1. Буквы не должны повторяться. Используя принцип умножения, получаем произведение: . Такое произведение достаточно сложно использовать в дальнейшем, и информация задачи представлена в ней в скрытой форме. В комбинаторике используют для таких произведений формулу размещений. Чтобы получить формулу размещений, умножим это произведение на единицу, которую представим следующим образом: 1 = = = = = А ‑ формула для размещений.

2. Буквы повторяются. Используя принцип умножения, получаем: 303030303030 = 306 = Ã – формула для размещений с повторениями.

Ответ: 1) А; 2) Ã.

5. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?

Необходимо посчитать, сколько существует трехзначных, четырехзначных и пятизначных чисел, составленных из этих пяти цифр. Трехзначных чисел — 543 = А, четырехзначных – 5432 = А, пятизначных – 54321 = А. Используем принцип сложения: А+ А + А = 60 + 120 + 120 = 300.

II. На использование формул для перестановок и размещений

1. Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять:

(а) из восьми букв, (б) из семи букв, (в) из трех букв?

В слове фрагмент 8 букв алфавита.

(а) Всевозможные перестановки 8 букв по восьми местам: А = =P8.

(б) Размещения 8 букв по 7 местам: А.

(в) Размещения 8 букв по 3 местам: А.

2. Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, а) если первая из них не равна нулю; б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?

а) Всего существует 10 цифр. На первом месте не может быть цифры 0, поэтому способов поставить цифру на первое место существует 9. На втором месте может стоять любая из 10-ти цифр (цифры могут повторяться), т. е. способов поставить цифру на второе место существует 10, и т. д. Используя принцип умножения, получаем: 910101010 = 9104 =9Ã.

б) На первом месте может стоять любая из 26 букв. На остальных местах — любые из девяти цифр, причем они могут повторяться. Используя принцип умножения, получаем: 269999=26Ã.

Ответ: 9Ã, 26Ã.

3. Сколькими способами можно расставить на полке семь книг, если (а) две определенные книги должны всегда стоять рядом, (б) эти две книги не должны стоять рядом?

(а) Книги, которые должны стоять рядом, считаем за одну книгу. Тогда нужно расставить 6 книг по шести местам. Применяя формулу перестановок, получаем: P6 = 6!. Мы учли перестановки шести книг, не учитывая порядок внутри тех книг, которые мы посчитали за одну. А так как две книги по двум местам можно разместить только двумя способами (P2), то получаем окончательно следующее произведение: P2P6 =2 6! = 1440.

(б) Способов переставить 7 книг существует P7= 7!. Из них ‑ 26! способов поставить определенные книги вместе. Следовательно, способов поставить книги так, чтобы 2 заданные книги не стояли вместе существует: 7! ‑ 26!.

Ответ: 1440; . 7! ‑ 26!

III. На использование формул для сочетаний

1. Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

Для решения этой задачи необходимо использовать формулу для сочетания элементов, т. к. здесь не имеет значения порядок элементов в выборке. Запишем формулу для сочетаний и произведем вычисления:

С = .

2. Компания из двадцати мужчин разделяется на три группы, в первую из которых входят три человека, во вторую — пять и в третью — двенадцать. Сколькими способами они могут это сделать? (Ответ записать в виде произведения сомножителей, не вычисляя его.)

Из 20-ти элементов необходимо сделать три выборки, причем порядок внутри выборок значения не имеет. Поэтому используем формулу для сочетаний. Чтобы выбрать из 20-ти элементов 3, существует С способов. Остается 17 элементов, из которых выбирается 5 элементов — С способами. Остается 12 элементов, из которых выбирается 12 элементов. Это можно сделать С = 1, т. е. одним способом. Используя принцип произведения, получаем: С С С.

Ответ: С С С.

3. Сколькими способами можно отобрать несколько фруктов из семи яблок, четырех лимонов и девяти апельсинов? (Мы считаем, что фрукты одного вида неразличимы.)

Т. к. фрукты одного вида неразличимы, то существует один способ взять одно яблоко, один способ взять 2 яблока, один способ взять три яблока и т. д., т. е. всего семь способов выбрать несколько яблок (несколько – это не менее одного). Необходимо также прибавить один способ не взять ни одного яблока. Следовательно, существует 8 способов взять яблоки. Аналогично существует 5 способов выбрать лимоны и 10 способов выбрать апельсины. Следуя принципу умножения, получим все способы отбора фруктов: 7510. Но среди этих способов существует один способ, когда не выбирается ни один фрукт. Следовательно, решением данной задачи будет следующее выражение: 7510 – 1 = 349.

IV. На использование формул для перестановок и сочетаний

1. Сколько четырехбуквенных слов можно образовать из букв слова сапфир? 2) Сколько среди них таких, которые не содержат буквы р? 3) Сколько таких, которые начинаются с буквы с и оканчиваются буквой р?

1. Из шести букв составляются четырехбуквенные слова, причем порядок букв важен для образования новых слов. Поэтому используется формула для размещений: А.

2. Необходимо исключить букву р из рассмотрения. Количество слов, не содержащих эту букву: А.

3. На первое место поставить букву с можно только одним способом. На последнее место поставить букву р можно тоже только одним способом. Остаются 4 буквы, которые необходимо разместить по двум местам: А.

2. Сколько пятибуквенных слов, каждое из которых состоит из трех согласных и двух гласных, можно. образовать из букв слова уравнение?

В слове уравнение 3 согласных и 4 гласных буквы русского алфавита. Чтобы посчитать количество требуемых пятибуквенных слов, необходимо посчитать количество сочетаний 3 согласных из 3-х заданных и двух гласных из четырех заданных: С и С. После того, как 5 букв выбраны, необходимо посчитать все возможные перестановки этих букв: С С P5.

Ответ: СС P5.

V. На использование формул для перестановок и сочетаний с повторениям

1. Сколько различных перестановок можно образовать изо всех букв слова перестановка? Сколько из них начинается с буквы п и оканчивается буквой а?

В слове перестановка 12 букв, из них повторяются 2 буквы е и две буквы а. Число перестановок из 12 элементов вычисляется с помощью формулы P12. Но среди этих перестановок будут повторяющиеся, в которых буквы е или а меняются местами. Чтобы не считать такие перестановки, используется формула для перестановок с повторениями: = .

Чтобы посчитать количество перестановок, начинающихся на букву п и оканчивающихся на букву а, необходимо исключить эти элементы и места, на которых они стоят из рассмотрения. Остается 10 букв и десять мест, причем остается только одна повторяющаяся буква е. Применяем формулу для перестановок с повторениями:

= .

Ответ: , .

Источник