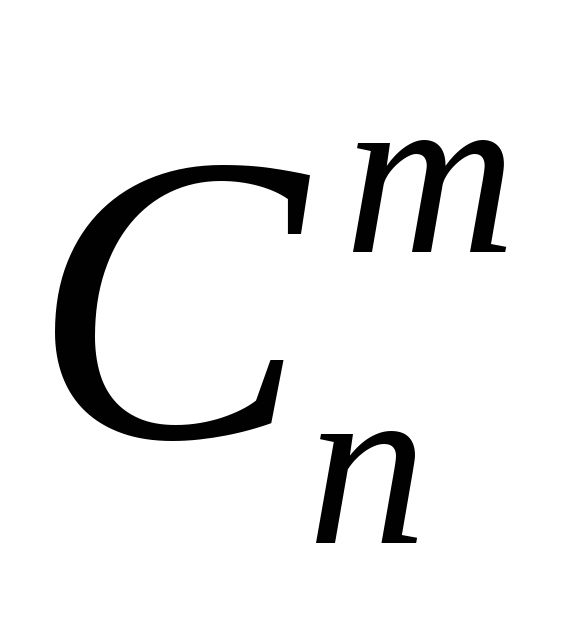Скількома способами можна з 30 учнів вибрати трьох чергових

Сполучення (комбінації) без повторень

Перевірка лекційного матеріалу (фронтальне опитування)

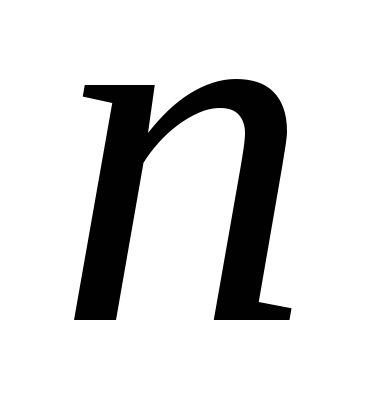
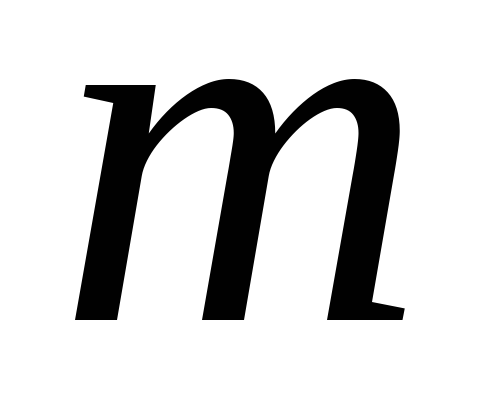
Дайте означення сполучення з елементів по .

Запишіть формули за якими знаходиться

Запишіть основні властивості комбінацій

Задача 1. Скількома способами можна вибрати трьох чергових із класу, у якому 20 учнів ?

Розв’язання. 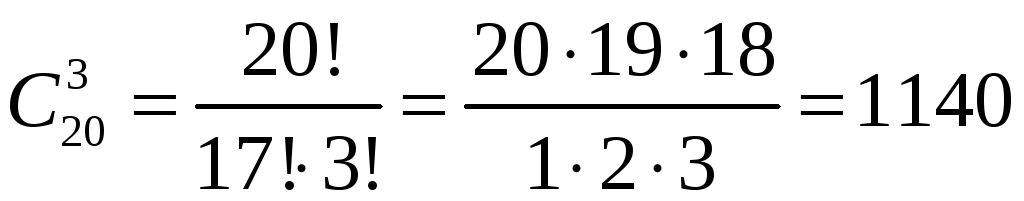способами.

Задача 2. Скількома способами можна роздати 6 різних предметів трьом особам так, щоб кожна отримала по 2 предмета ?

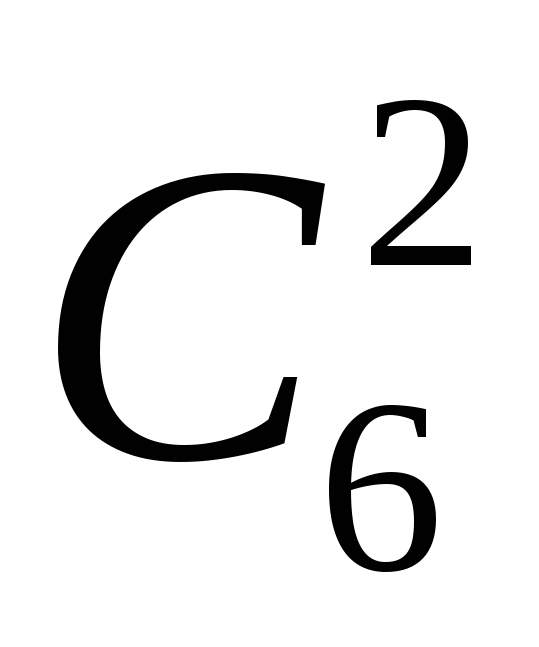
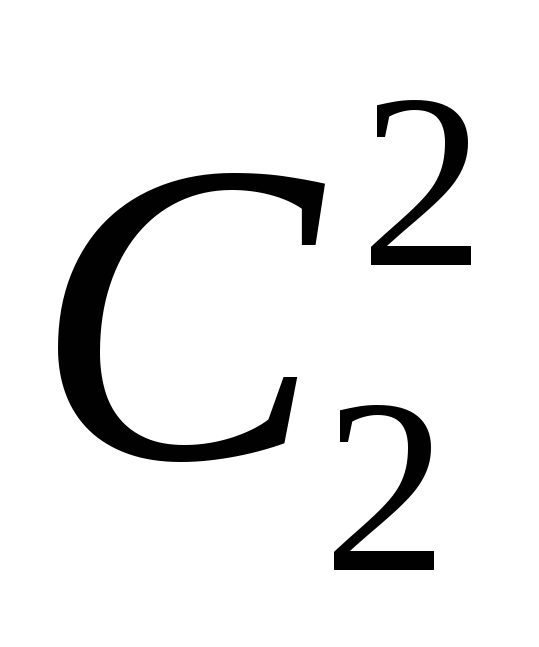
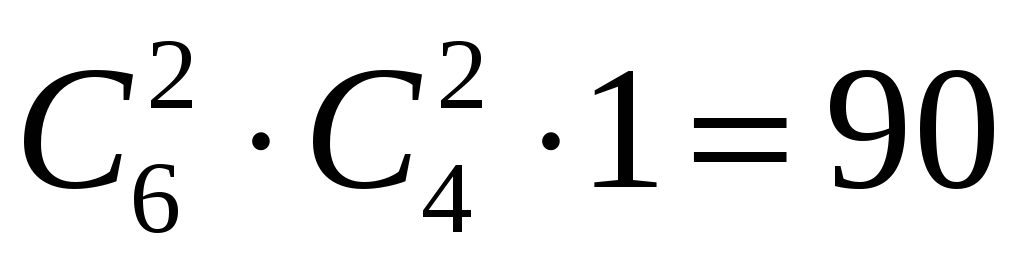
Розв’язання. Перша особа може вибрати довільні два предмети з шести способами; друга може вибрати два предмети з чотирьох, що залишилися, способами; а третя візьме два останніх предмета =1 способом. За правилом добутку всього способів.

Задача 3. Скількома способами можна вибрати 2 олівця і 3 ручки з 6 різних олівців і 8 різних ручок ?

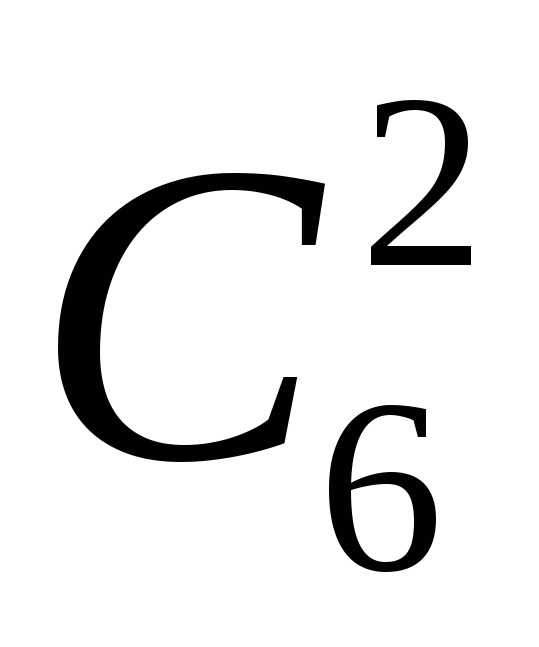
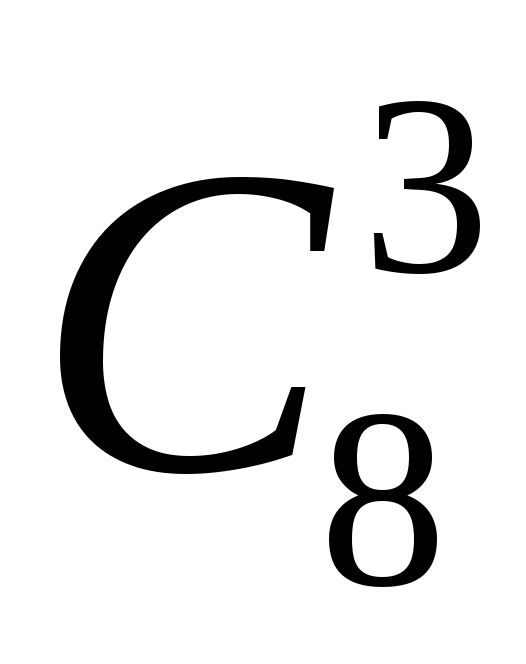
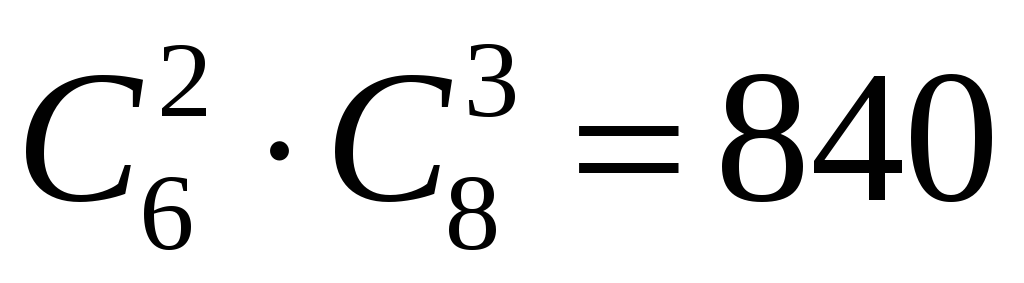
Розв’язання. Олівці можна вибрати способами, а ручки способами. Отже, всього є способів.

Задача 4. Скільки різних звукосполучень можна взяти на десяти вибраних клавішах рояля, якщо кожне звукосполучення може містити від трьох до десяти звуків ?

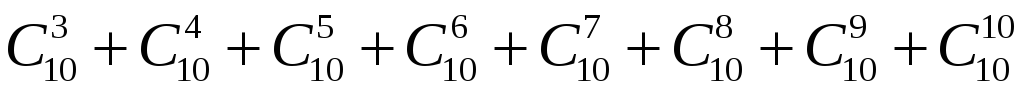
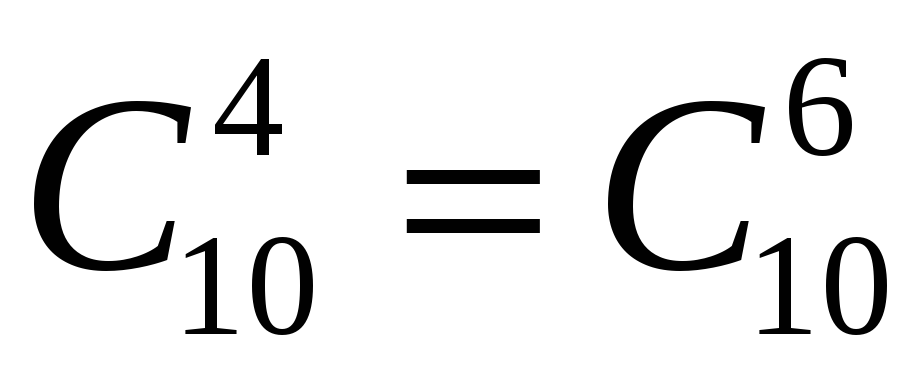
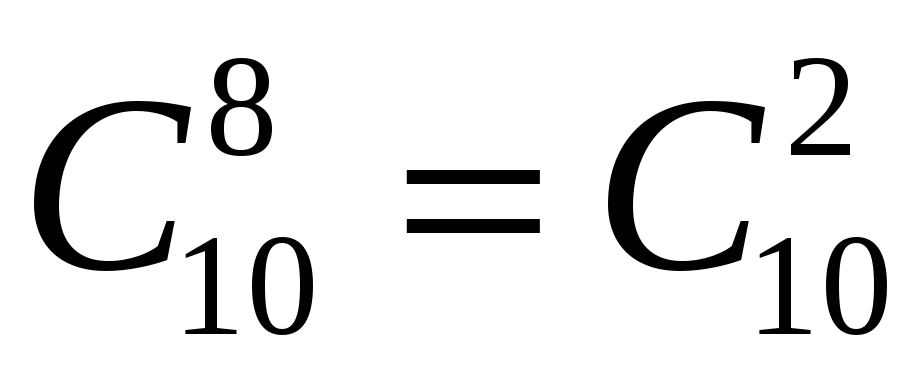
Розв’язання. Очевидно, що нам потрібно знайти суму . Застосуємо властивість комбінації. Маємо: , , , . Тому шукана кількість звукосполучень дорівнює способів.

Задача 5. В колоді 36 карт, з них 4 тузи. Скількома способами можна вибрати 6 карт так, щоб серед них було рівно 2 тузи ?

Розв’язання. Виберемо два тузи з чотирьох способами, а ще чотири карти виберемо з 32 , що залишилися, способами. За правилом добутку остаточно маємо, що способів вибору буде .

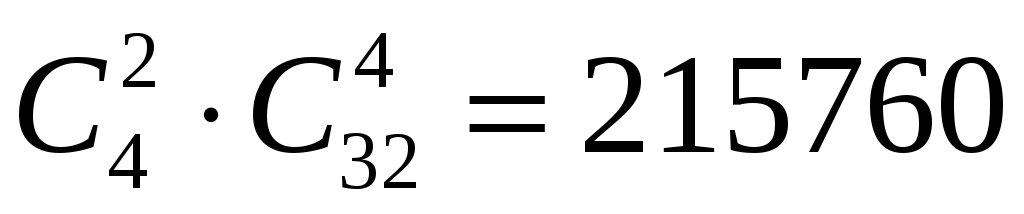
Задача 6. У вазі стоять пронумеровані 10 червоних і 5 рожевих гвоздики. Скількома способами можна вибрати з вази: а) три квітки; б) три квітки одного кольору; в) три квітки так, щоб серед них були як червоні, так і рожеві гвоздики ?

Розв’язання. а) =455 способами, б) Можна вибрати три червоних гвоздики способами, або три рожевих способами. За правилом суми маємо способів вибору, в) Можна вибрати дві червоні і одну рожеву гвоздики способами, або одну червону і дві рожеві гвоздики способами. Отже, всього способів буде .

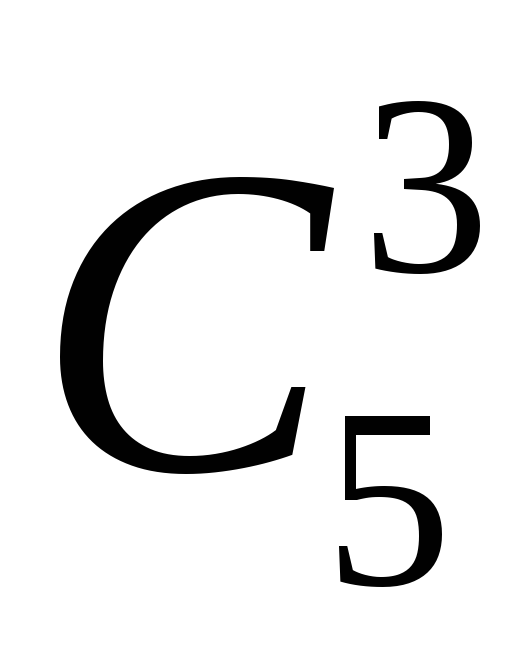
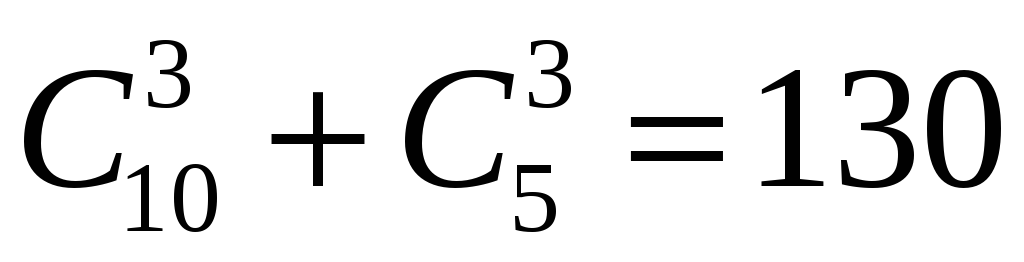
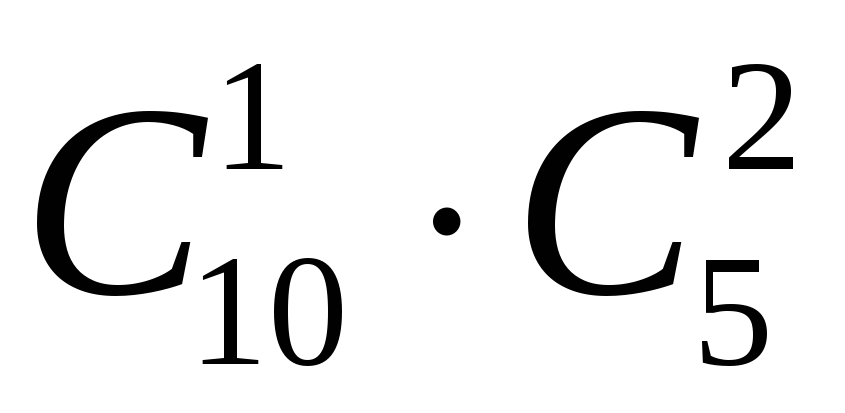
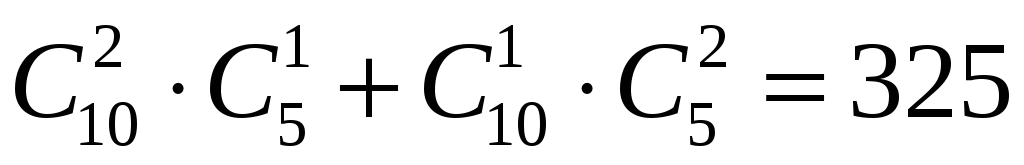
Задача 7. З групи, в яку входять 7 хлопчиків, і 4 дівчини, треба скласти команду з 6 чоловік так, щоб вона містила не менше двох дівчинок. Скільки є способів скласти таку команду ?

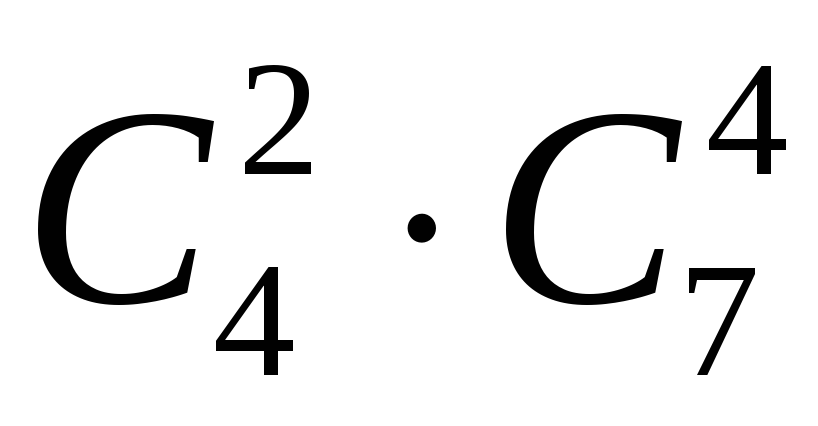
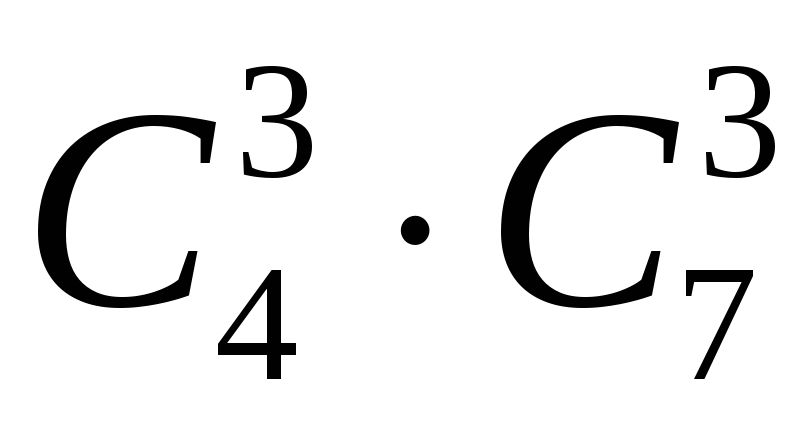
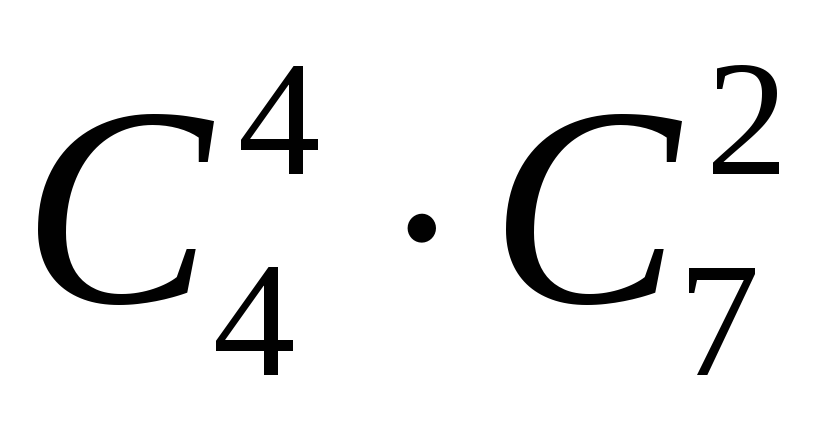
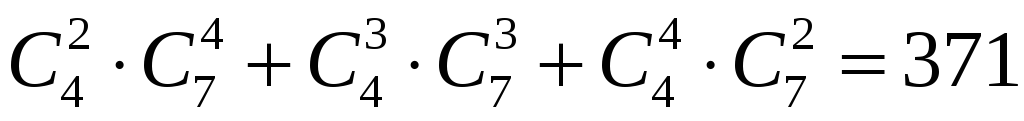
Розв’язання. Якщо в команді 2 дівчини і 4 хлопця, то маємо способів; якщо по 3 дівчини і хлопця, то способів; якщо ж 4 дівчини і 2 хлопця, то способів. За правилом суми всього маємо спосіб.

Задача 8. Скільки різних добутків, кратних 10, можна дістати з чисел 2,3,5,7,11,13 ?

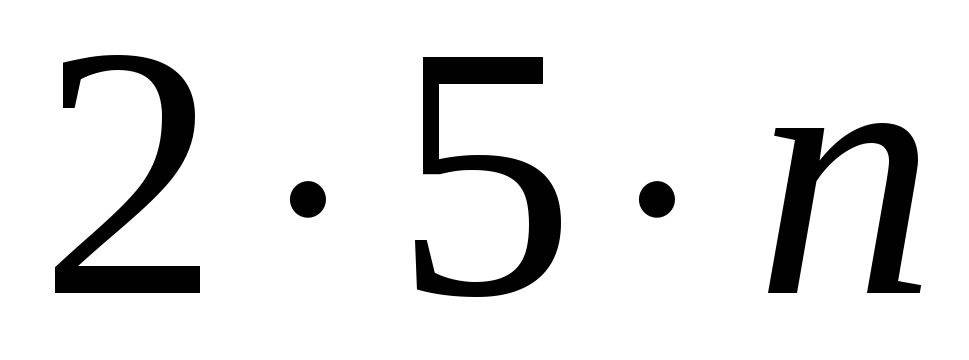
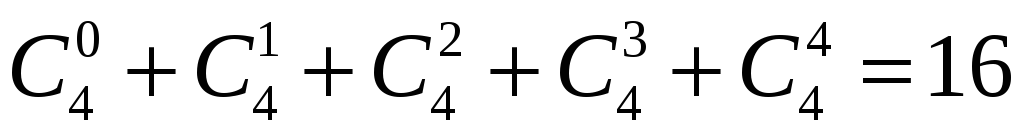
Розв’язання. Будемо складати добутки, кратні 10 , у вигляді , де п всі можливі добутки з чисел 3,7,11,13. В число п можуть включатись від 0 до 4 множників. Отже, всіх можливих добутків, що задовольняють умові, буде .

Задача 9. Скільки різних дільників має число 2310?

Розв’язання. Оскільки 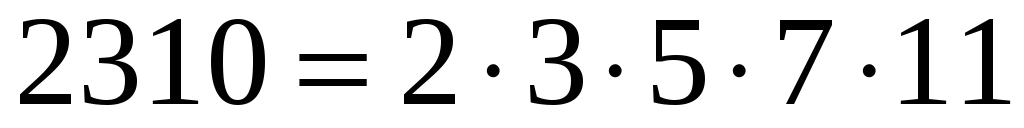, то число d буде дільником 2310, якщо d  добуток чисел з набору 2,3,5,7,11. Будемо складати всі можливі добутки з цих чисел(вони містять від 1 до 5 множників) і додамо дільник даного числа 1. Отримаємо, що число 2310 має дільники.

Источник

Комбінаторика

У готелі є 50 номерів, із них — 17 — економ-класу, 18 — класу «Стандарт», а решта — класу «Люкс». Скількома способами можна вибрати номер класу «Стандарт» або класу «Люкс»?

Виберіть випадкову подію.

Після літа наступить осінь.

У крокодила виросли крила.

Завтра піде дощ.

У слові «кіт» немає літери «А».

Скільки тризначних чисел можна записати цифрами 0, 1, 2, 3, 4, якщо кожну з цих цифр можна використовувати не більше одного разу?

Скільки чотирицифрових чисел можна скласти з чисел 1, 2, 3, 4, 5, якщо цифри в числі не повторюються?

Скільки трицифрових чисел можна скласти з чисел 1, 2, 0, якщо цифри в числі не повторюються?

Якщо деякий елемент А можна вибрати k₁ способами, а елемент В (незалежно від вибору елемента А) – k₂ способами, то скількома способами можна вибрати А або В?

Скільки трицифрових чисел можна скласти з чисел 1, 2, 3, якщо цифри в числі можуть повторюватися?

Скільки трицифрових чисел можна скласти з чисел 1, 2, 0, якщо цифри в числі можуть повторюватися?

Скількома способами можна з 30 учнів вибрати трьох чергових?

Скількома способами можна розсадити 6 учнів за круглим столом?

Із цифр 1,2,3,4,5 складають всеможливі числа, кожне з яких складається не більше ніж з 3 цифр. Скільки таких чисел можна утворити, якщо повторення цифр не дозволяється?

Скількома способами можна скласти список з 9 осіб?

Із класу, в якому навчаються 18 учнів, вибирають трьох делегатів на шкільну конференцію. Скількома способами це можна зробити?

1. Скільки прямих ліній можна провести через 7 точок, з яких ніякі три не лежать на одній прямій?

PIN-код мобільного телефону складається з 4-х цифр. Скільки різних варіантів PIN-коду існує, якщо вони складаються лише з одиниць і двійок?

Студент на першому курсі повинен вибрати одну з трьох іноземних мов, яку вивчатиме, та одну з п’яти спортивних секцій, що відвідуватиме. Скільки всього існує варіантів вибору студентом іноземної мови та спортивної секції?

Источник

Элементы комбинаторики

Приклад 5. Команда із трьох членів виступає на змаганнях, у яких беруть участь ще 15 спортсменів. Скількома способами можуть бути розподілені місця, що посіли члени цієї команди, за умови, що жодне місце не може бути поділене?

Розв’язання . Усьоговзмаганняхберутьучасть18спортсменів. Будемо з 18 наявних місць вибирати 3 для членів даної команди.

A 18 3 =18 17 16 =4896.

Приклад 6. Якою буде кількість способів розподілу місць у попередній задачі, якщо відомо, що жоден із членів даної команди не посів місце нижче десятого?

Розв’язання . Вибираємо три місця із десяти, що залишилися.

A 10 3 =10 9 8 =720 .

Приклад 7. Скільки різних трицифрових натуральних чисел можна скласти із запропонованого набору цифр за умови, що жодна цифра в кожному із цих чисел не повторюється?

а) Із п’ятиелементної множини складатимемо різні трьохелементні підмножини.

б) усього трицифрових чисел буде A 5 3 =60, але нас не задовольняють числа, які починаються з нуля, таких чисел буде A 4 2 (до першої цифри «0» приєднуватимемо різні двохелементні підмножини, які складаються з чотирьох цифр, що залишилися). Разом: A 5 3 − A 4 2 =60−12=48 чисел.

Відповідь : а) 60; б) 48.

Приклад 8. Скільки різних натуральних чисел, які містять не більше ніж три знаки, можна скласти з цифр 2, 4, 6, 8?

Розв’язання . «Не більше ніж» означає, що числа можуть бути одно-, або дво-, або трицифровими. За правилом суми маємо

A 4 1 + A 4 2 + A 4 3 =4+4 3+4 3 2=4+12+24 =40 чисел.

Приклад 9. Скільки різних натуральних чисел можна скласти із цифр 0, 1, 2, 3, щоб до кожного такого числа кожна із цих цифр входила не більше одного разу?

Розв’язання . Ми вже розв’язували схожу задачу (див. приклад 7, б), проте тепер складемо одно-, дво-, три- і чотирицифрові числа. Одноцифрових: A 3 1 ; двоцифрових — A 4 2 − A 3 1 ; трицифрових — A 4 3 − A 3 2 ; чотирицифрових — A 4 4 − A 3 1 .

Усього чисел — A 3 1 + A 4 2 − A 3 1 + A 4 3 − A 3 2 + A 4 4 − A 3 3 = 48 .

Приклад 10. (Узагальнена задача.) Скільки є різних упорядкованих підмножин множини, що складається з n елементів?

Відповідь : A n 1 + A n 2 + A n 3 +…+ A n n .

Задачі для самостійного розв’язування

1. У команді 12 членів. Скількома способами можна вибрати

в ній капітана і воротаря?

2. Скільки словників треба видати, щоб можна було безпосередньо виконувати переклади з кожної із п’яти мов: російської, англійської­ , французької, німецької та іспанської на будь-яку іншу з цих мов?

3. Розклад одного дня містить 5 уроків. Визначте кількість таких розкладів при виборі з 11 предметів і за умови, що один предмет займає один урок. Як зміниться розв’язування задачі, якщо відомо, що першим уроком обов’язково має бути математика?

4. Скількома способами можна вибрати з повної колоди карт (52 шт.) по одній карті кожної масті за умови, що серед вийнятих карт немає жодної пари однакових, тобто двох королів, двох дам і т. д.?

5. Скільки різних дробів, що не дорівнюють одиниці, можна скласти з чисел 3, 5, 7, 11, 13, 17, 19, 23 так, щоб до кожного дробу входило два числа? Скільки серед них буде правильних?

6. Чотири біатлоністи з України брали участь у чемпіонаті світу. Скількома способами могли бути розподілені місця, які посіли представники України, якщо:

а) жоден із них не посів місце нижче п’ятнадцятого, і жодне місце не було поділено;

б) жоден із них не посів призового місця, а всього було 15 учасників чемпіонату?

7. Скільки різних чотирицифрових натуральних чисел можна скласти із цифр:

а) 2, 3, 5, 7, 9; б) 0, 2, 3, 5, 7, 9?

8. Скількирізнихчотирицифровихпарнихчиселможнаскласти із цифр:

а) 1, 3, 5, 7, 8; б) 2, 4, 6, 8, 9?

9. Людина має 10 друзів і протягом декількох днів запрошує двох із них у гості так, що кожен побував у неї в гостях тільки один раз. Скільки різних варіантів зустрічей вона може скласти?

10. Людина має 10 друзів і щодня запрошує декількох із них

у гості (або одного), але в різний час. Скільки варіантів прийому гостейвонаможескласти,якщожоднігрупигостейнеповторюються?

11. Скільки різних натуральних чисел можна скласти із цифр

Стислі теоретичні відомості

• • Перестановкою із n елементів називається будь-яка впорядкована множина з усіх цих елементів, причому дві такі множини вважаються різними, якщо вони відрізняються між собою порядком елементів.

Читають: кількість перестановок із n елементів.

Зрозуміло, що кількість перестановок із n елементів — це число розміщень із n елементів по n елементів, тобто вибір різних n -елеметних підмножин із n -елементної множини, кожні дві з яких відрізняються порядком елементів.

P n = A n n = ( n n − ! n ) ! = n 0! ! = n 1 ! = n !

Приклад. Скількома способами можна розставити в шеренгу 10 людей?

Розв’язання . Маємо різні перестановки з 10 елементів:

Приклади розв’язування задач

Приклад 1. Скількома способами можна розставити на полиці 5 книг?

Відповідь : P 5 =5!

Приклад 2. Скільки нових «слів» можна скласти з букв слова: а) «цукат»; б) «ручник»?

Відповідь : а) P 5 =5! ; б) P 6 =6!

Приклад 3. Скільки чотирицифрових чисел можна скласти із запропонованого набору цифр, не повторюючи їх?

Источник