ВАРІАНТ 6
1. На базі відпочинку 70 чоловік. З них 27 займаються в драмгуртку, 32 співають в хорі, 22 захоплюються спортом. В драмгуртку 10 чоловік з хору, в хорі 6 спортсменів, в драмгуртку 8 спортсменів; 3 спортсмени відвідують й драмгурток, й хор. Скільки чоловік не співають в хорі, не захоплюються спортом та не займаються в драмгуртку? Скільки чоловік зайняті лише спортом?
2. Скільки різних натуральних чисел можна скласти з цифр,0,1,2,3,4, щоб в кожне таке число кожна з цих цифр входила не більше одного разу?
3. У вазі стоять пронумеровані 10 червоних і 5 рожевих гвоздики. Скількома способами можна вибрати з вази: а) три квітки; б) три квітки одного кольору; в) три квітки так, щоб серед них були як червоні, так і рожеві гвоздики?
4. Ліфт, в якому знаходяться 9 пасажирів, може зупинитись на десяти поверхах. Пасажири виходять групами по два, три і чотири чоловіки. Скількома способами вони можуть вийти, якщо ліфт не повертається на поверх, де він вже був?
5. Десять тенісистів мають бути розподілені в групи по 2,3 і 5 спортсменів для поїздки на три турніри, які обираються з 6 можливих. Скількома способами це можна зробити? Скількома способами можна розділити 6 різних цукерок між трьома дітьми?
6. Скількома способами можна розкласти 28 різних предметів по чотирьох ящиках, так, щоб в кожному ящику опинилося по 7 предметів?
7. В поштовому відділенні продаються листівки 10 сортів. Скількома способами можна купити в ньому 12 листівок?
Источник
ВАРІАНТ 2



1. На одній з кафедр університету працює 13 чоловік, кожен з них знає хоча б одну іноземну мову. 10 чоловік знають англійську, 7 – німецьку, 6 – французьку, 5 – англійську та німецьку, 4 – англійську та французьку, 3 – німецьку та французьку. Скільки чоловік:
1) знають всі три мови,
2) знають рівно дві мови,
знають лише англійську?
2. Команда з п’яти чоловік виступає в змаганнях, в яких бере участь ще 20 спортсменів. Скількома способами можуть бути розподілені місця, зайняті членами цієї команди, при умові, що жодне місце на цих змаганнях не може бути поділено?
3. Садівник повинен протягом трьох днів посадити 10 дерев десяти різних порід. Скількома способами він може розподілити за днями свою роботу, якщо буде висаджувати не менше одного дерева в день?
4. Ліфт, в якому знаходяться 9 пасажирів, може зупинитись на десяти поверхах. Пасажири виходять групами по два, три і чотири чоловіки. Скількома способами вони можуть вийти, якщо ліфт не повертається на поверх, де він вже був?
5. Десять тенісистів мають бути розподілені в групи по 2,3 і 5 спортсменів для поїздки на три турніри, які обираються з 6 можливих. Скількома способами це можна зробити?
6. Скількома способами можна розділити 6 різних цукерок між трьома дітьми?
7. Скількома способами можна розкласти 28 різних предметів по чотирьох ящиках, так, щоб в кожному ящику опинилося по 7 предметів?
8. В поштовому відділенні продаються листівки 10 сортів. Скількома способами можна купити в ньому 12 листівок?
9. Знайдіть показник бінома 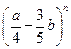
Источник
ВАРІАНТ 6



1. На базі відпочинку 70 чоловік. З них 27 займаються в драмгуртку, 32 співають в хорі, 22 захоплюються спортом. В драмгуртку 10 чоловік з хору, в хорі 6 спортсменів, в драмгуртку 8 спортсменів; 3 спортсмени відвідують й драмгурток, й хор. Скільки чоловік не співають в хорі, не захоплюються спортом та не займаються в драмгуртку? Скільки чоловік зайняті лише спортом?
2. Скільки різних натуральних чисел можна скласти з цифр,0,1,2,3,4, щоб в кожне таке число кожна з цих цифр входила не більше одного разу?
3. У вазі стоять пронумеровані 10 червоних і 5 рожевих гвоздики. Скількома способами можна вибрати з вази: а) три квітки; б) три квітки одного кольору; в) три квітки так, щоб серед них були як червоні, так і рожеві гвоздики?
4. Ліфт, в якому знаходяться 9 пасажирів, може зупинитись на десяти поверхах. Пасажири виходять групами по два, три і чотири чоловіки. Скількома способами вони можуть вийти, якщо ліфт не повертається на поверх, де він вже був?
5. Десять тенісистів мають бути розподілені в групи по 2,3 і 5 спортсменів для поїздки на три турніри, які обираються з 6 можливих. Скількома способами це можна зробити? Скількома способами можна розділити 6 різних цукерок між трьома дітьми?
6. Скількома способами можна розкласти 28 різних предметів по чотирьох ящиках, так, щоб в кожному ящику опинилося по 7 предметів?
7. В поштовому відділенні продаються листівки 10 сортів. Скількома способами можна купити в ньому 12 листівок?
8. Знайдіть середній член розкладу 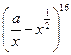
Источник
ВАРІАНТ 14



1. В класі 40 чоловік. З них з англійської мови трійки мають 19 чоловік, з математики – 17, з фізики – 22. Лише з одного предмета мають трійки: з фізики – 11, з англійської – 4, з математики – 4. 7 чоловік мають трійки й з математики, й з фізики, з них 5 чоловік мають трійки й з англійської.
Скільки чоловік навчаються без трійок?
Скільки чоловік мають лише по дві трійки?
2. Учасники шахового турніру грають в залі, де є 8 столів. Скількома способами можна розмістити шахістів, якщо учасники всіх партій відомі?
3. Скільки існує різних нескоротних дробів, чисельниками і знаменниками яких є числа 2,3,5,7,11,13,17,19?
4. Ліфт, в якому знаходяться 9 пасажирів, може зупинитись на десяти поверхах. Пасажири виходять групами по два, три і чотири чоловіки. Скількома способами вони можуть вийти, якщо ліфт не повертається на поверх, де він вже був?
5. Десять тенісистів мають бути розподілені в групи по 2,3 і 5 спортсменів для поїздки на три турніри, які обираються з 6 можливих. Скількома способами це можна зробити?
6. Скількома способами можна розділити 6 різних цукерок між трьома дітьми?
7. Скількома способами можна розкласти 28 різних предметів по чотирьох ящиках, так, щоб в кожному ящику опинилося по 7 предметів?
8. В поштовому відділенні продаються листівки 10 сортів. Скількома способами можна купити в ньому 12 листівок?
9. Розв’яжіть рівняння 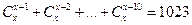
Источник
Математика 5 клас
Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ
§ 14. Комбінаторні задачі
Комбінаторика — розділ математики, який вивчає комбінації і перестановки предметів, розміщення елементів, що мають певні властивості тощо. Розглянемо задачу.
Задача 1. На пошті в продажу є 5 різних конвертів і 3 різні марки. Скількома способами можна купити конверт з маркою?
Розв’язання. 1-й спосіб. Намалюємо дерево можливих варіантів (рис. 5). Позначимо конверт буквою К, марку — буквою М. Малюємо від стовбура 5 гілок (оскільки є 5 видів конвертів). Оскільки маємо 3 марки, то від кожної з п’яти отриманих точок
малюємо по 3 гілки. Рахуємо кількість отриманих внизу точок — 15 і отримуємо відповідь до задачі. Дерево можливих варіантів дає змогу розв’язувати різноманітні задачі, пов’язані з обчисленням кількості способів.
2-й спосіб. Оберемо конверт. У комплект до нього можна вибрати будь-яку з трьох марок. Тому є 3 комплекти, що містять обраний конверт. Оскільки конвертів усього 5, то кількість різних способів становить 15 (5 ∙ 3 = 15).
Дійшли до важливого правила комбінаторики — правила добутку:
якщо елемент А можна обрати m способами, а після кожного такого вибору інший елемент В можна обрати (незалежно від вибору елемента А) n способами, то пару елементів А і В можна обрати m ∙ n способами.
Правило добутку можна використовувати, якщо треба обрати більше 2 елементів.
Задача 2. На пошті в продажу є 5 різних конвертів, 3 різні марки і 4 різних вітальні листівки. Скількома способами можна купити комплект, що містить конверт, марку та листівку?
Розв’язання. 5 ∙ 3 ∙ 4 = 60 способів.
Розглянемо далі задачу, у якій треба полічити кількість способів, якими можна розмістити в ряд певну кількість предметів.
Задача 3. Дитина грається трьома іграшками: машиною, трактором, кораблем. Скількома способами їх можна викласти в ряд?
Розв’язання. На перше місце можемо поставити одну з трьох іграшок: машину, трактор або корабель. Після цього на друге місце можна поставити одну з двох наступних іграшок. Після цього на третє місце ставимо одну іграшку, яка залишилася після вибору перших двох. Використовуючи правило добутку, знайдемо, що іграшки можна розмістити шістьма різними способами (3 ∙ 2 ∙ 1). Перевіримо розв’язок задачі за допомогою дерева можливих варіантів (рис. 6).
Обчислили кількість способів, якими можна розмістити в ряд кілька предметів. Такі розміщення називають перестановками, вони відіграють велику роль у комбінаториці.
Позначають перестановки буквою Р. У задачі 3 кількість перестановок з трьох елементів дорівнює Р3 = 1 ∙ 2 ∙ 3; аналогічно кількість перестановок з двох елементів Р2 = 1 ∙ 2; із чотирьох елементів Р4 = = 1 ∙ 2 ∙ 3 ∙ 4 = 24; з п’яти Р5 = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120 і т. д.
Розглянемо ще кілька комбінаторних задач.
Задача 4. З даних чисел вибрати такі, які при перестановці цифр утворюють числа, у яких число одиниць на 3 більше за число десятків: 42, 36, 74, 14, 85, 92, 47.
Розв’язання. Переставляючи цифри, маємо числа 24, 63, 47, 41, 58, 29, 74. Умову задовольняють числа 74 та 85.
Задача 5. В алфавіті племені БАБА є тільки дві літери «а» і «б». Запиши всі слова цього племені, що містять: 1) дві літери; 2) три літери.
Розв’язання. 1) аа, ба, аб, бб (усього чотири слова); 2) ааа, ааб, аба, абб, ббб, бба, баб, баа (усього вісім слів). Зауважимо, що знайдена кількість слів узгоджується з правилом добутку. Оскільки на кожне місце є два «претенденти» — «а» і «б», то слів, що містять дві літери, має бути 2 ∙ 2 = 4, а три літери — 2 ∙ 2 ∙ 2 = 8.
Розглянемо дві задачі на знаходження конфігурації елементів, що мають певні властивості.
Задача 6. У клітинки квадрата (рис. 7) треба поставити числа 1, 2, 3 та 4 так, щоб числа не повторювалися ні в рядках, ні в стовпчиках, ні по діагоналях (лініях, що ведуть з лівого нижнього кута в правий верхній та з правого нижнього кута в лівий верхній).
Розв’язання. Один з варіантів розв’язання подано на рисунку 8.
Задача 7. Скількома способами можна розділити 5 цукерок між трьома дітьми так, щоб кожна дитина отримала хоча б по одній цукерці?
Розв’язання. Подамо розв’язок у вигляді таблиці. Отже, всього є 6 способів.
Источник











