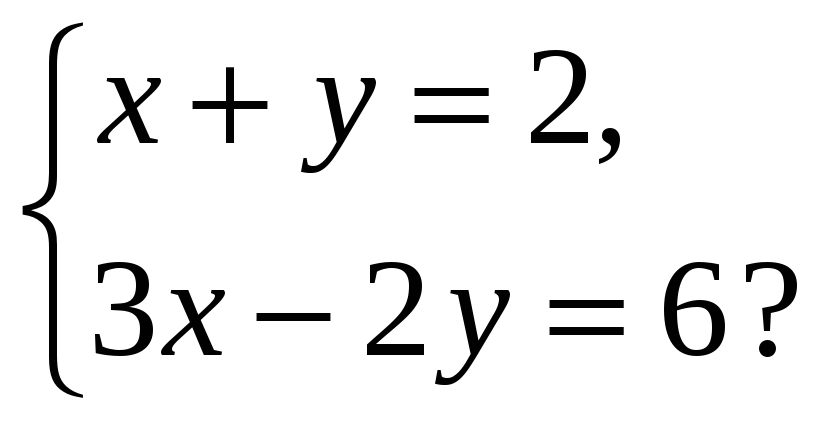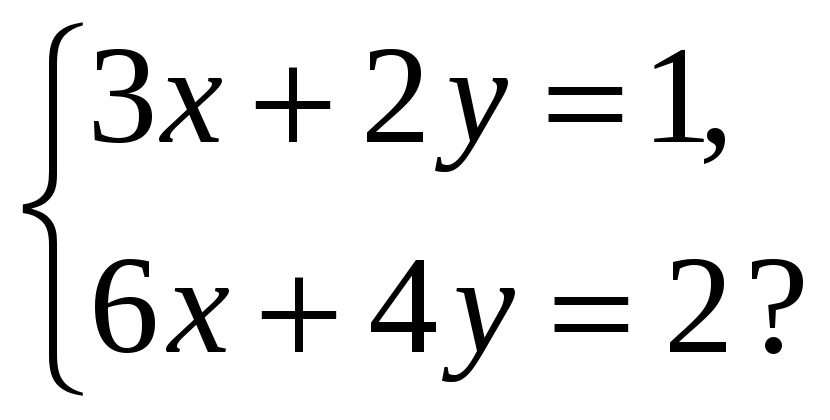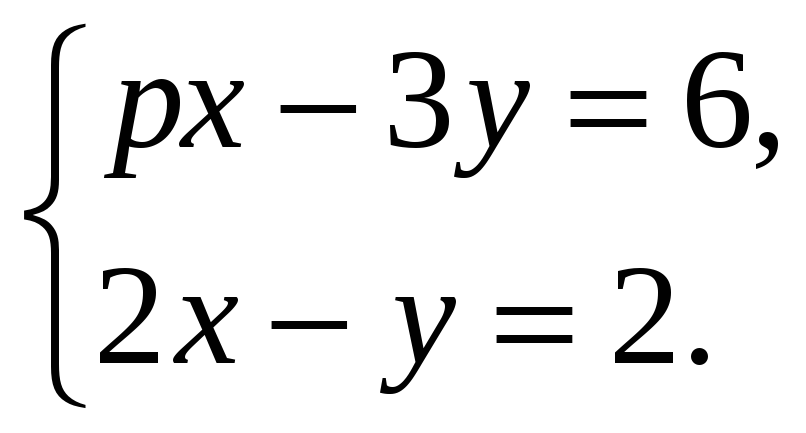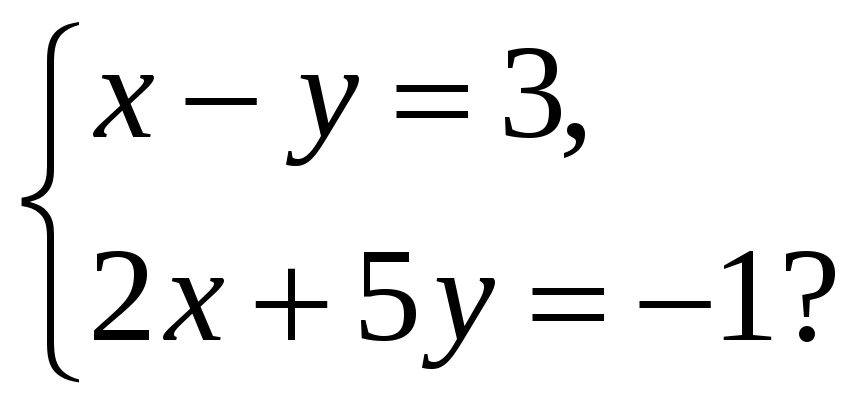- Проверочная работа по теме Графический способ решения СЛУ 7 класс
- Просмотр содержимого документа «Проверочная работа по теме Графический способ решения СЛУ 7 класс»
- Самостоятельная работа «Решение систем линейных уравнений»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Проверочная работа по теме Графический способ решения СЛУ 7 класс

Проверочная работа по теме Графический способ решения СЛУ 7 класс
Просмотр содержимого документа
«Проверочная работа по теме Графический способ решения СЛУ 7 класс»
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 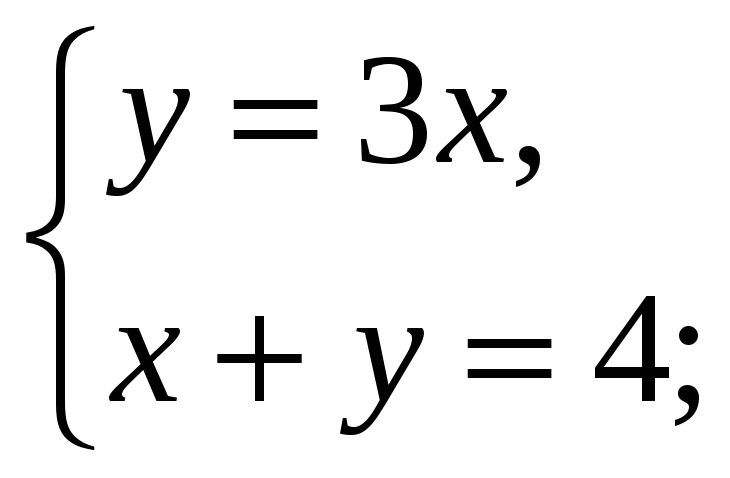
3. Сколько решений имеет система уравнений
а) 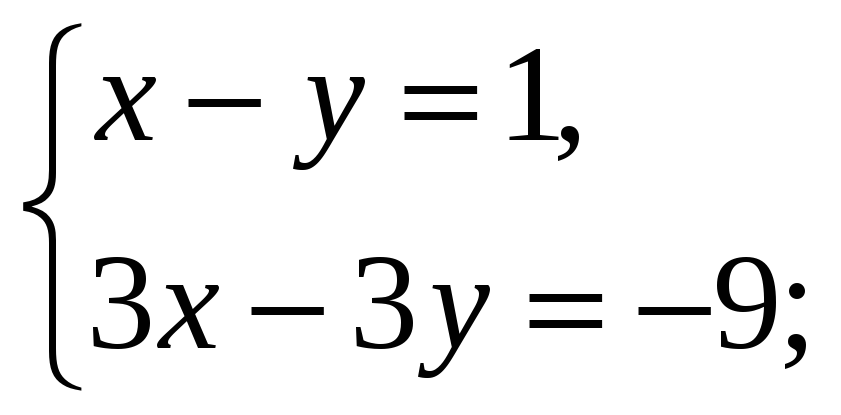
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 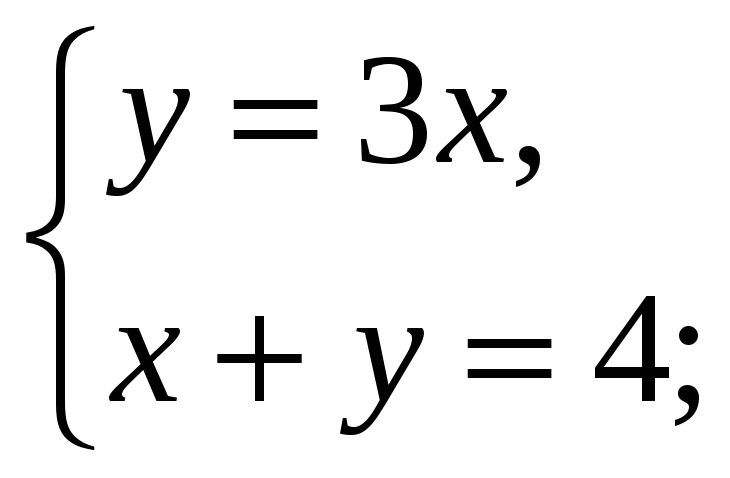
3. Сколько решений имеет система уравнений
а) 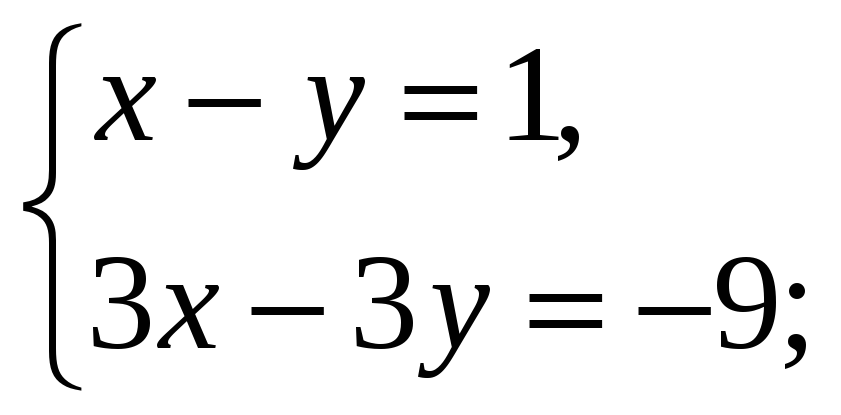
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 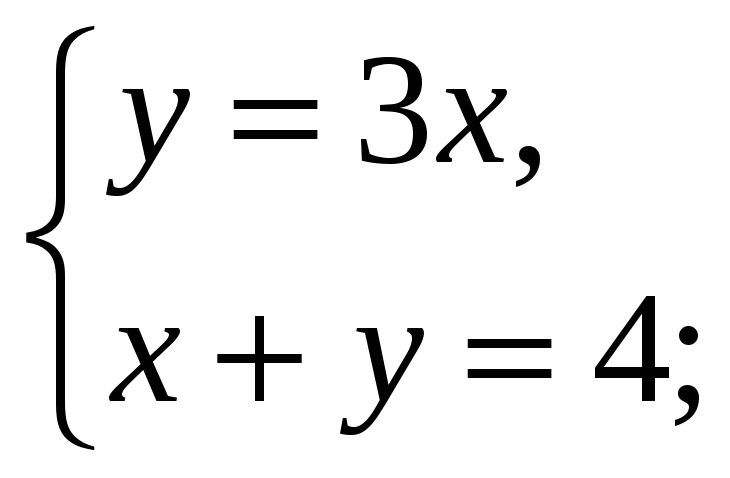
3. Сколько решений имеет система уравнений
а) 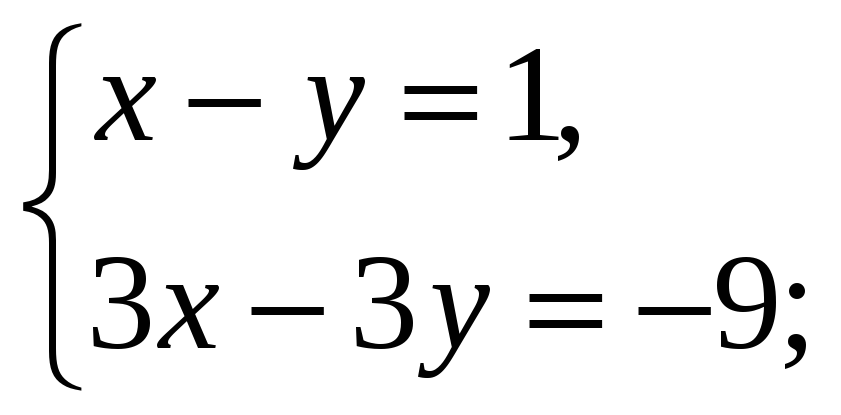
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 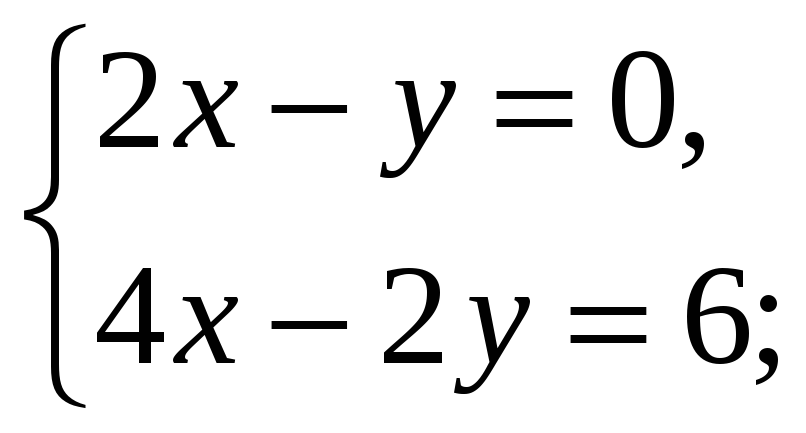
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 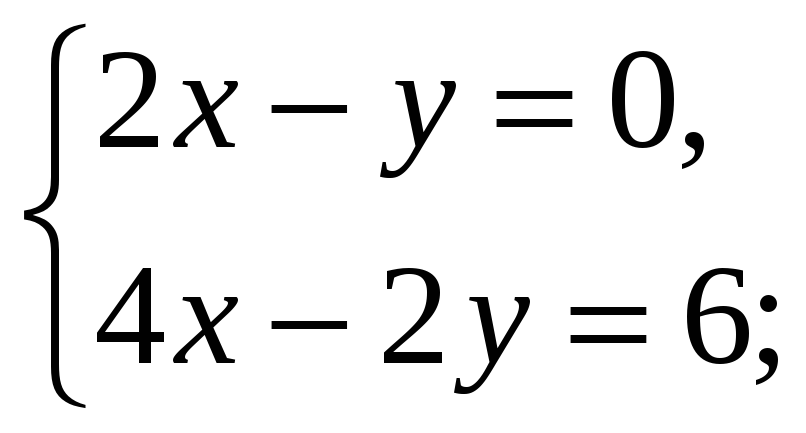
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 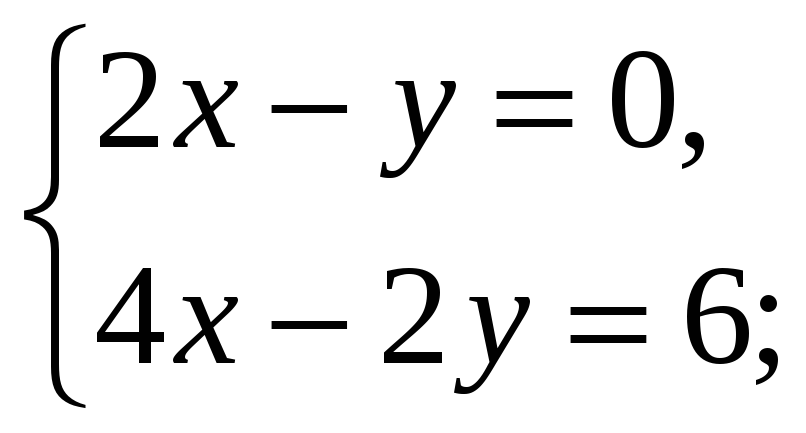
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
Источник
Самостоятельная работа «Решение систем линейных уравнений»
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом подстановки:
а)
б)
в)
Решите систему уравнений методом сложения:
а)
б)
в)
Решите систему уравнений методом сложения:
а)
б)
в)
Решите систему уравнений методом сложения:
а)
б)
в)
Решите систему уравнений методом сложения:
а)
б)
в)
Решите систему уравнений методом сложения:
а)
б)
в)
Решите систему уравнений методом сложения:
а)
б)
в)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 798 человек из 78 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 284 человека из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 602 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-416187
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Российский совет олимпиад школьников намерен усилить требования к олимпиадам
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Вопрос о QR-кодах для сотрудников школ пока не обсуждается
Время чтения: 2 минуты
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
Российские адвокаты бесплатно проконсультируют детей 19 ноября
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник