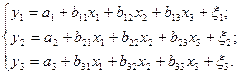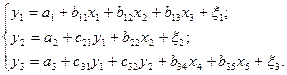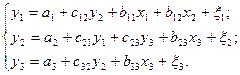Системы эконометрических уравнений классифицируются по способу

Виды систем эконометрических уравнений

Тема 5. Системы эконометрических уравнений

Ввиду многогранности экономические процессы наиболее полно могут быть описаны с помощью системы эконометрических уравнений.

Системы эконометрических уравнений подразделяются на следующие виды:

i. системы независимых уравнений;

ii. системы рекурсивных уравнений;

iii. системы одновременных уравнений.

Система независимых уравнений представляет собой систему, в которой эндогенные переменные (у₁,у₂, … , у_n) рассматриваются как функции объясняющих переменных (х₁, х₂, …, х_m). Каждое уравнение такой системы является уравнением регрессии, нахождение параметров которого может быть осуществлено МНК. Это значит, что каждое уравнение системы независимых уравнений рассматривается самостоятельно, и в системе из n уравнений n раз применяется МНК.

Пример системы независимых уравнений, содержащей три эндогенных переменных и три экзогенных переменных:

Система рекурсивных уравнений представляет собой систему, в которой эндогенная переменная одного уравнения системы в каждом последующем уравнении является фактором наряду с другими факторами.

Пример системы рекурсивных уравнений:

где а – свободные члены в каждом уравнении;

b_ij – коэффициенты при х в i-м уравнении при j-м факторе х;

с_ik — коэффициенты при у в i-м уравнении при k-м у.

В рекурсивной модели в качестве объясняющих переменных в правой части модели могут участвовать только те эндогенные переменные, которые ранее были определены в предыдущих уравнениях системы.

Каждое уравнение рекурсивной модели можно рассматривать самостоятельно, а оценку параметров производить с помощью обычного МНК.

Система одновременных уравнений (взаимозависимых) представляет собой систему, в которой результативный признак одного уравнения системы входит во всех другие уравнения системы в качестве фактора наряду с другими факторами.

Для нахождения параметров системы одновременных уравнений не может быть применен МНК, поэтому требуются другие специальные методы.

Источник

Классификация систем эконометрических уравнений

Система уравнений в эконометрических исследованиях может быть построена по-разному.

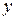
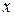
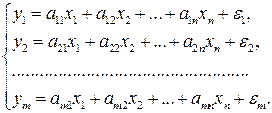
Возможна система независимых уравнений, когда каждая зависимая переменная рассматривается как функция одного и того же набора факторов :

(2.1)

Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки .

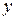
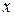
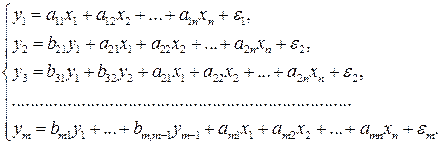
Если зависимая переменная одного уравнения выступает в виде фактора в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:

(2.2)

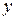
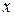
В данной системе зависимая переменная включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов . Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:

(2.3)

Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

В рассмотренных классах систем эконометрических уравнений структура матрицы коэффициентов при зависимых переменных различна.

Представим систему эконометрических уравнений в матричном виде:

где B – матрица коэффициентов при зависимых переменных;

Y – вектор зависимых переменных;

Г— матрица параметров при объясняющих переменных;

X — вектор объясняющих переменных;

E – вектор ошибок.

Если матрица В диагональная, то рассматриваемая модель является системой независимых уравнений. Так, при трех зависимых и трех объясняющих переменных модель имеет вид:

Матрица параметров при зависимых переменных является диагональной:

Если матрица В треугольная (или может быть приведена к такому виду), то модель представляет собой систему рекурсивных уравнений. Так, если модель имеет вид:

т.е. зависимая переменная y₁ первого уравнения участвует как объясняющая переменная во втором уравнении системы, а зависимая переменная y₂ второго уравнения рассматривается как объясняющая переменная в третьем уравнении. Тогда матрица коэффициентов при зависимых переменных модели составит:

,

т.е. представляет собой треугольную матрицу.

Если матрица В не является ни диагональной, ни треугольной, то модель представляет собой систему одновременных уравнений. Так, для модели вида

получим матрицу коэффициентов при зависимых переменных:

,

которая не является ни диагональной, ни треугольной. Соответственно то отражается на выборе метода оценки параметров эконометрических систем.

Источник

Общие понятия о системах уравнений, используемых в эконометрике

#Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками…

-определения случайных воздействий

-однородности выборочной совокупности

#Система эконометрических уравнений систему …

-систему экономических показателей

-систему социальных показателей

#Основной задачей построения систем эконометрических уравнений является описание …

+структуры связей реальной экономической системы

-взаимодействия реальных экономической и политической систем

-структуры связей реальной политической системы

#Основным преимуществом использования систем эконометрических уравнений является …

+возможность описания сложных систем

-построение изолированных уравнений регрессии

-исследование связи между двумя признаками

-исследование связи между моделируемым показателем и рядом влияющих на него факторов

#Система эконометрических уравнений не используется при моделировании …

+взаимосвязей временных рядов данных

-механизма функционирования экономических систем

-связей между экономическими показателями

#Для моделирования сложных экономических систем целесообразно использовать …

+систему эконометрических уравнений

-изолированное уравнение регрессии

#Первопричиной использования систем эконометрических уравнений является то, что …

+изолированное уравнение не отображает истинные влияния факторов на вариацию результативных переменных

-существует доминирующий фактора

-отсутствует связь между экономическими показателями

-случайные факторы оказывают существенное влияние на моделируемую экономическую систему

#Изолированное уравнение множественной регрессии может быть использовано для моделирования взаимосвязи экономических показателей, если …

+факторы не взаимодействуют друг с другом

-система не предполагает использование уравнений множественной регрессии

-при изменении одного экономического показателя другие факторы также изменяются

-при изменении переменной влечет за собой изменения во всей системе взаимосвязанных признаков

#При изучении взаимодействия спроса и предложения целесообразно использовать …

+систему эконометрических уравнений

-уравнение зависимости спроса от цены

-уравнение зависимости предложения от цены

#Система эконометрических уравнений предполагает наличие …

+нескольких зависимых и нескольких независимых признаков

-нескольких зависимых и одного независимого признаков

-одного зависимого и нескольких независимых признаков

-одного зависимого и совокупности независимых признаков

#При построении системы эконометрических уравнений необходимо учитывать …

+структуру связей реальной экономической системы

-среднюю величину каждой зависимой переменной

-максимальную величину каждого фактора

#Структурной формой модели называется система …

-уравнений с фиксированным набором факторов

#Система независимых уравнений предполагает …

+совокупность независимых уравнений регрессии

-совокупность зависимых уравнений регрессии

-одно изолированное уравнение регрессии

-совокупность независимых временных рядов

#В левой части системы взаимозависимых переменных, как правило, находится …

+несколько зависимых переменных

-одна независимая переменная

-несколько зависимых переменных и случайная величина

-одна зависимая переменная

#В левой части системы независимых уравнений находится …

+одна зависимая переменная

-одна независимая переменная

-совокупность зависимых переменных

-совокупность независимых переменных

#Система рекурсивных уравнений включает в каждое …

+последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений с набором собственно факторов

-предыдущее уравнение в качестве факторов все зависимые переменные последующих уравнений с набором собственно факторов

-уравнение в качестве факторов все зависимые переменные с набором собственно факторов

-последующее уравнение в качестве зависимых переменных собственно факторы предшествующих уравнений

#Система взаимозависимых уравнений в ее классическом виде называется также системой _______ уравнений

#Системы эконометрических уравнений классифицируются по …

+способу вхождения зависимых и независимых переменных в уравнения регрессии

-количеству факторов в каждом уравнении системы

-количеству уравнений в системе

-способу ранжирования факторов в зависимости от силы влияния на моделируемые показатели

#Выделяют три класса систем эконометрических уравнений: …

+системы независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений

-системы одновременных уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений

-система независимых уравнений, системы изолированных уравнений и системы рекурсивных уравнений

-системы взаимозависимых уравнения, системы рекурсивных уравнений и системы возвратных уравнений

#В системе независимых уравнений каждое уравнение представлено …

+изолированным уравнением регрессии

-уравнением временного ряда

-рекурсивным уравнением регрессии

-совместным уравнением регрессии

#В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как …

+сумма количества зависимых переменных предыдущих уравнений и количества независимых факторов

-сумма количества зависимых переменных последующих уравнений и количества независимых факторов

-разность количества зависимых переменных предыдущих уравнений и количества независимых факторов

-разность количества зависимых переменных последующих уравнений и количества независимых факторов

#При построении систем независимых уравнений набор факторов в каждом уравнении определяется числом факторов, оказывающих ___________ на моделируемый показатель

-оказывающих как существенное, так и несущественное влияние

-оказывающих несущественное влияние

-не оказывающих существенное влияние на моделируемый показатель

#В правой части структурной формы взаимозависимой системы могут стоять _______ переменные

#Структурной формой модели называется система _______ уравнений

#Структурными коэффициентами модели называются коэффициенты _________ в структурной форме модели

+при экзогенных и эндогенных переменных

-только при экзогенных переменных

-только при эндогенных переменных

#Приведенная форма модели представляет собой систему …

+линейных функций эндогенных переменных от экзогенных

-нелинейных функций эндогенных переменных от экзогенных

-случайных функций эндогенных переменных от экзогенных

-обратных функций эндогенных переменных от экзогенных

#Под идентификационной моделью подразумевается …

+единственность соответствия между приведенной и структурной формами модели

-существование нескольких приведенных моделей для одной структурной формы

#Модель идентифицируема, если число параметров структурной формы модели …

+равно числу параметров приведенной формы модели

-меньше числа параметров приведенной формы модели

-больше числа параметров приведенной формы модели

-равно числу уравнений модели

#Приведенная форма модели получена из _______ формы модели …

#Эндогенными переменными являются …

-переменные, значение которые определяется вне системы

#Экзогенными переменными являются …

-переменные, значение которые определяется внутри системы

#Эндогенными переменными не являются …

-переменные y в уравнениях системы вида у = f(x)

-переменные, значение которые определяется внутри системы

#Экзогенными переменными не являются …

-переменные х в уравнениях системы вида у = f(x)

-переменные, значение которые определяется вне системы

#Косвенный метод наименьших квадратов применим для …

+идентифицируемой системы одновременных уравнений

-любой системы одновременных уравнений

-неидентифицируемой системы уравнений

-неидентифицируемой системы рекурсивных уравнений

#Косвенный метод наименьших квадратов требует …

+преобразования структурной формы модели в приведенную

-линеаризации уравнений структурной формы модели

-нормализации уравнений структурной формы

-линеаризации уравнений приведенной формы

#Двухшаговый метод наименьших квадратов применим для решения …

+системы одновременных уравнений в качестве наиболее общего метода решения

-только сверхидентифицированной системы одновременных уравнений

-только идентифицированной системы одновременных уравнений

-неидентифицированной системы одновременных уравнений

#Двухшаговый метод наименьших квадратов применяется для оценки параметров …

+систем эконометрических уравнений

-нелинейных уравнений регрессии

-линеаризованных уравнений регрессии

#В приведенной форме модели в правой части уравнений находятся …

+только независимые переменные

-зависимые и независимые переменные

-только зависимые переменные

#Для оценки коэффициентов структурной формы модели не применяют _____ метод наименьших квадратов

#При оценке параметров приведенной формы модели косвенный метод наименьших квадратов использует алгоритм…

+обычного метода наименьших квадратов

-метода максимального правдоподобия

-метода главных компонент

-расчета средней взвешенной величины

#Двухшаговый метод наименьших квадратов предполагает ______ использование обычного МНК

-не использовать обычный МНК

#На первом этапе применения косвенного метода наименьших квадратов …

+структурную форму преобразуют в приведенную

-приведенную форму преобразуют в структурную

-проводят процедуру линеаризации структурной формы модели

-проводят процедуру линеаризации приведенной формы модели

#При оценке параметров систем одновременных уравнений не производят …

+линеаризацию уравнений системы

-преобразование структурной формы модели в приведенную

-расчет коэффициентов приведенной формы

-идентификацию системы одновременных уравнений

#Приведенная форма модели является результатом преобразования …

Источник