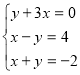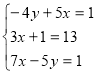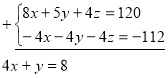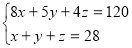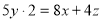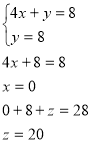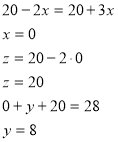Систему рівнянь за трьома способами

Тема 9. Розв’язування найпростіших систем трьох рівнянь з трьома змінними

Розробка циклу уроків однієї з навчальних тем курсу алгебри „Системи лінійних рівнянь з двома змінними» для 7 класу. Дев’ятий урок із даної теми

Тема 9.

Розв’язування найпростіших систем трьох рівнянь з трьома змінними

Мета: поглибити навички розв’язування систем лінійних рівнянь з двома невідомими способом підстановки та додавання; розвивати логічне мислення, культуру математичних записів, виховувати вміння аналізувати; пояснити алгоритм розв’язування систем 3-х лінійних рівнянь з трьома невідомими.

Тип уроку: формування умінь і навичок

1. Організаційний момент. Перевірка домашнього завдання. Усебічна перевірка ступеня засвоєння змісту навчального матеріалу.
2. Підготовка учнів до активного й усвідомленого засвоєння навчального матеріалу.
3. Постановка пізнавального завдання. Пояснення нового матеріалу.
4. Засвоєння нових способів дій.
5. Первинна перевірка і корекція засвоєння учнями нового матеріалу.
6. Закріплення знань і способів дій.
7. Підсумки уроку. Повідомлення домашнього завдання.
8. Рефлексія. Створення „Пам’ятки”. Діти разом із вчителем здійснюють покрокову деталізацію розв’язування системи з трьома невідомими(алгоритм).

Учні на дошці розв’язують домашні вправи, решта – приклади.

№1

Розв’яжіть графічно систему рівнянь:

№2

При якому значенні k пряма y = kx – 4 проходить через точку перетину прямих y =2 x – 5 i y =- x +1?

№3

Чи має розв’язок система рівнянь:

№4

Чи проходять прямі 2х+3у=20, 3х – 5у=11 і х+у=9 через одну і ту саму точку?

№5

Чи існує на прямій 7х+8у=135 точка:

• абсциса якої дорівнює її ординаті;
• абсциса протилежна її ординаті;
• ордината якої дорівнює подвоєній абсцисі?

Серед математичних задач є чимало економічних, розв’язання яких часто зводиться до розгляду системи лінійних рівнянь з ба ­ гатьма змінними.

Розглянемо декілька задач.

Задача 1. Завод повинен переслати замовникам 1200 деталей. Деталі упаковують у ящики трьох видів: по 80, по 50 і по 40 деталей. Скільки ящиків і якого виду повинен використати завод?

У задачі треба визначити три невідомі числа; число ящиків по 80, по 50 i по 40 деталей.

Позначимо число ящиків першого, другого і третього видів через х, у і z . Тоді 80 x , 50у і 40 z — кількість деталей у ящиках першого, другого і третього видів.

За умовою задачі

80х + 50у + 40 z = 1200, або 8х + 5у + 4 z = 120. (1).

Рівняння розв’язується методом простого перебору. Надаючи, наприклад, двом довільним змінним певних значень, дістаємо від ­ повідне значення третьої змінної. Певну кількість розв’язків цього рівняння можна подати у вигляді такої таблиці:

Заповніть таблицю.

Що ви можете сказати про значення змінних, що містяться в таблиці?

Чи всі вони є розв’язками рівняння ( 1 )?

Які значення х, у і z задовольняють умову задачі?

Поміркувавши над цими запитаннями, можемо дати таку від ­ повідь. Одне рівняння з трьома змінними х, у і z може мати безліч розв’язків. Проте далеко не всі з них задовольняють умову задачі практичного змісту, оскільки змінні х, у і z — натуральні числа.

Задача 2 . Завод повинен переслати замовникам 1200 деталей, які треба упакувати в 28 ящиків трьох видів: на 80, 50 i 40 деталей. Скільки ящиків кожного виду можна використати?

Залишивши ті самі позначення, що й у першій задачі, діста ­ немо те саме рівняння:

80 x + 50у + 40 z = 120 або 8х + 5у + 4 z = 120.

Однак, крім цього, з умови задачі випливає, що х + у + z = 28. Отже, маємо систему двох рівнянь з трьома змінними:

(2)

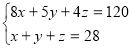
Цікаво, чи система має розв’язок? Якщо має, то скільки їх?

Для розв’язування цієї системи застосуйте спосіб алгебричного додавання. У результаті ви одержите таке розв’язання:

Вам уже відомо , що рівняння з двома змінними має безліч розв’язків.

Оскільки значення змінних х і у згідно з умовою задачі є на ­ туральними числами і х + у + z = 28, то рівняння 4х+у= 8 має такі розв’язки: (0; 8), (1; 4), (2; 0).

Користуючись розв’язками рівняння 4х+у=8, самостійно знайдіть розв’язки системи (2) за умови, що х, у і z — натуральні числа і х+у+г=28.

Задача 3. Завод повинен переслати замовникам 1200 деталей, які треба упакувати в 28 ящиків трьох видів; на 80, 50 і 40 деталей, причому третю частину деталей треба упакувати в ящики по 50 де ­ талей. Скільки ящиків і якого виду повинен використати завод?

Залишивши ті самі позначення, дістанемо, як і раніше, рів ­ няння:

Проте за умовою задачі можемо скласти ще й третє рівняння, а саме:

Отже, маємо систему трьох рівнянь з трьома змінними:

(3)

Подумайте, як розв’язати систему (3).

Спробуйте розв’язати цю систему, застосовуючи спосіб алгеб ­ ричного додавання або підстановки.

Спосіб алгебраїчного додавання

; ; ;

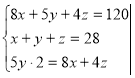
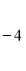
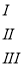
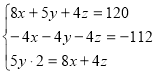
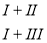
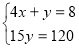
Спосіб підстановки

; ; ;

; ;

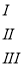
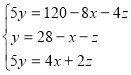
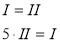
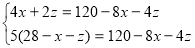
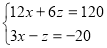
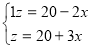
Отже, розв’язком даної системи трьох рівнянь з трьома змін ­ ними є трійка чисел: (0; 8; 20).

IV . Робота із Експертом у середовищі «Системи лінійних рівнянь» .

V . Розв’язування завдань

№№1 – 5.

; ; ; ; ;

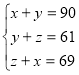
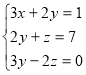
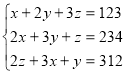
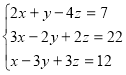
1. Розв’язування систем з трьома невідомими, попередньо зі складеної задачі. Вчитель допомагає учням скласти рівняння(якщо у цьому виникне потреба).

№1

Сума кутів А і В трикутника АВС дорівнює 110°, а сума кутів А і С — 120°. Знайдіть кути трикутника АВС.

№2

На літніх Олімпійських іграх у Барселоні спортсмени Ук ­ раїни здобули 40 медалей. Золотих і срібних – 31 спортсмен, а срібних і бронзових – 23 спортсмени. Скільки золотих, срібних і бронзових медалей одержали спортсмени України?

№3

Пропонуємо завдання, якими перевіряється кмітливість та швидкість мислення. Над рискою вказана залежність між трьома швидкостями. Під рискою потрібно визначити залежність між двома швидкостями.

а). 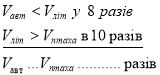б).

в). г).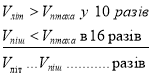

Визначте швидкості літака, автомобіля і птаха, якщо швидкість пішохода 4 км/год.

№4

Три села А, В і С розміщені так, що шлях від А до С через В дорівнює 12,5 км, а від В до А через С — 15,5 км і від С до В через А — 9 км. Знайдіть відстань між селами.

№5

Периметри трьох граней прямокутного паралелепіпеда, що мають спільну вершину, дорівнюють відповідно 172, 178 І 202 см. Знайдіть площу поверхні цього паралелепіпеда та його об’єм.

№6

Знайдіть сторони трикутника, якщо його периметр дорів ­ нює 90 см, більша сторона менша від суми двох інших сторін на 10 см, а потроєна менша сторона на 2 см більша від суми двох сторін.

№7

Сума цифр трицифрового числа дорівнює 21. Якщо в цьому числі поміняти місцями цифру сотень і цифру десятків, то число зменшиться на 180, а якщо поміняти місцями цифру десятків і цифру одиниць, то число збільшиться на 36. Знайдіть це трицифрове число.

№8

Сума цифр трицифрового числа дорівнює 16. Якщо в цьому числі поміняти місцями цифру сотень і цифру одиниць, то число зменшиться на 297, а якщо цифру сотень з першого місця пере ­ ставити на останнє, залишивши інші цифри на своїх місцях, то число зменшиться на 477. Знайдіть це трицифрове число.

№9

Периметр трикутника дорівнює 16 дм. Більша сторона дов ­ ша за меншу на 25 см, а подвоєна середня сторона менша від суми двох інших сторін на 1 см. Знайдіть сторони трикутника.

№10

У трьох посудинах 54 л води. Якщо з першої посудини перелити у другу 4 л, то в обох посудинах буде води порівну, а якщо з третьої посудини перелити у другу 17 л, то в другій буде в чотири рази більше води, ніж у третій. Скільки води в кожній посудині?

№11

У трьох посудинах 36 л води. З першої посудини перелили половину води в другу, потім третю частину води з другої посудини перелили в першу. Після цього в усіх посудинах води стало порівну. Скільки води було в кожній посудині спочатку?

№12

Дорога з М до К завдовжки 90 км веде на гору, рівниною і з гори. Велосипедист їхав з М до К 5,5 год, а назад — 6 год. Швидкість велосипедиста, коли він їхав на гору, була 12 км/год, на горизонтальній ділянці шляху — 18 км/год, а з гори — 20 км/год. Визначте довжину трьох відтинків дороги: на гору, рівниною і з гори.

2. Робота у середовищі «Системи лінійних рівнянь» .

VII . Підсумки уроку. Повідомлення домашнього завдання.

Источник

Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Матричний метод. Метод оберненої матриці

Скориставшись цим онлайн калькулятором для розв’язання системи лінійних рівнянь (СЛР) матричним методом (методом оберненої матриці), ви зможете дуже просто і швидко знайти розв’язок системи рівнянь.

Скориставшись онлайн калькулятором для розв’язання системи лінійних рівнянь матричним методом (методом оберненої матриці) ви отримаєте детальний розв’язок вашого прикладу, який дозволить зрозуміти алгоритм розв’язання таких задач і закріпити вивчений матеріал.

Розв’язати систему лінійних рівнянь матричним методом

Змінити назви змінних в системі

Заповніть систему лінійних рівнянь:

Ввід даних в калькулятор для розв’язання системи лінійних рівнянь матричним методом

• В онлайн калькулятор можна вводити числа або дроби. Більш детально читайте в правилах вводу чисел.
• Для зміни в рівнянні знаків з «+» на «-» введіть від’ємне число.
• Якщо у вашому рівнянні відсутня яка-небудь змінна, то у відповідне поле в калькуляторі введіть нуль.
• Якщо в рівнянні попереду змінною відсутні числа, то в відповідне поле калькулятора введіть одиницю.

Наприклад, лінійне рівняння x ₁ — 7 x ₂ — x ₄ = 2

буде вводитися в калькулятор наступним чином:

Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь матричним методом

• Використовуйте кнопки , , та на клавіатурі, для переміщення між полями калькулятору.
• Замість x ₁, x ₂, . ви можете ввести власні назви змінних.

Вводити можна лише числа або дроби (-2.4, 5/7, . ). Більш детально читайте в правилах вводу чисел.

Источник