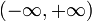Система штурма для многочлена способ ее построения

Ряд штурма

Ряд Штурма (система Штурма) для вещественного многочлена — последовательность многочленов, позволяющая эффективно определять количество корней многочлена на промежутке и приближённо вычислять их с помощью теоремы Штурма. Ряд и теорема названы именем французского математика Жака Штурма.

Содержание

Определение

Рассмотрим многочлен f(x) с вещественными коэффициентами. Конечная упорядоченная последовательность отличных от нуля многочленов с вещественными коэффициентами

называется рядом Штурма для многочлена f(x) , если выполнены следующие условия:

• не имеет корней;
• если и , то ;
• если , то произведение меняет знак с минуса на плюс, когда x , возрастая, проходит через точку c , т.е. когда существует такое δ > 0 , что для и для .

Иногда ряд Штурма также определяют как построенный определённым образом ряд Штурма.

Связанные определения

• Значением ряда Штурма в точке c называется количество смен знака в последовательности f₀(c),f₁(c). f_s(c) после исключения нулей.

Теорема Штурма

Пусть f(x) — ненулевой многочлен с вещественными коэффициентами, f₀(x),f₁(x). f_s(x) — некоторый ряд Штурма для него, [a,b] — промежуток вещественной прямой, причём . Тогда число корней многочлена f(x) на промежутке [a,b] равно W(a) − W(b) , где W(c) — значение ряда Штурма в точке c .

Построение

Ряд Штурма существует для любого ненулевого вещественного многочлена.
Пусть многочлен f(x) , отличающийся от константы, не имеет кратных корней. Тогда ряд Штурма для него можно построить, например, следующим образом:

• ;
• ;
• Если f_k(x) ( k > 0 ) имеет корни, то , где — остаток от деления многочлена f(x) на многочлен g(x) в кольце многочленов , иначе s = k .

Для произвольного многочлена, отличающегося от константы, можно положить

,

и далее следовать приведенному выше способу. Здесь (f(x),f ‘ (x)) — наибольший общий делитель многочленов f(x) и f ‘ (x) . Если многочлен f(x) есть ненулевая константа, то его ряд Штурма состоит из единственного многочлена f₀(x) = f(x) .

Применение

Ряд Штурма используется для определения количества вещественных корней многочлена на промежутке (см. теорему Штурма). Отсюда вытекает возможность его использования для приближённого вычисления вещественных корней методом двоичного поиска.

Пример

Построим указанным выше способом ряд Штурма для многочлена f(x) = (x − 1)(x − 3) = x 2 − 4x + 3

Многочлен fi(x)	Знак многочлена в точке
		0	1	2	3	4
f0(x) = x 2 − 4x + 3
f1(x) = 2x − 4
f2(x) = 1
Значение ряда в точке

Таким образом, по теореме Штурма число корней многочлена f(x) равно:

• 2 − 0 = 2 на промежутке
• 2 − 0 = 2 на промежутке (0,4)
• 2 − 1 = 0 на промежутке (0,2)

Источник

Теорема Штурма

Метод штурма и его применение

Изучение вопроса о вычислении корней полиномов когда-то составляло основное содержание высшей алгебры. В прикладных задачах важную роль играет также задача аппроксимации вещественных корней полинома путем указания их достаточно точных границ.

В данной статье рассматривается решение такого вопроса с помощью метода Штурма.

Для начала рассмотрим вопрос о границах действительных корней.

Существует несколько способов их нахождения. Изложим некоторые.

Пусть дан многочлен степени пусть будет верхней границей его положительных корней. Рассмотрим многочлены

и найдем верхние границы их положительных корней; допустим это будут соответственно числа , , . Тогда все положительные корни многочлена удовлетворяют неравенствам , все отрицательные корни неравенствам

Для определения верхней границы положительных корней можно применить метод Ньютона.

Пусть дан многочлен с действительными коэффициентами и положительным старшим коэффициентом Если при многочлен и все его последовательные производные принимают положительные значения, то число служит верхней границей положительных корней.

Пример. Применим метод Ньютона к многочлену . Мы имеем:

Все эти многочлены положительны при , что легко проверить хотя бы методом Горнера. Следовательно, число есть верхняя граница положительных корней многочлена .

Рассмотрим многочлен для нахождения нижней границы отрицательных корней исходного полинома (мы берем вместо потому, что для применимости метода Ньютона старший коэффициент должен быть положительным, на корни многочлена эта перемена знака не оказывает никакого влияния). Так как

а все эти многочлены положительны при , то число служит верхней границей положительных корней для , и поэтому число будет нижней границей отрицательных корней для .

Рассматривая, наконец, многочлены

мы найдем для них, применяя метод Ньютона, в качестве верхних границ положительных корней соответственно числа 1 и 4, а поэтому нижней границей положительных корней многочлена служит число , верхней же границей отрицательных корней число .

Следовательно, положительные корни многочлена расположены между числами и , отрицательные корни между числами и . [1, с. 244-246]

Определение 1. Конечная упорядоченная система отличных от нуля многочленов с действительными коэффициентами

где все многочлены, начиная с , являются остатками от деления двух предыдущих, взятых с противоположным знаком, называется системой (рядом) Штурма для многочлена , если выполняются следующие условия:

1. Любые два соседних полинома системы не имеют общих корней.
2. Если действительный корень промежуточного полинома системы, то предыдущий и последующий полиномы имеют разные знаки.
3. Если действительный корень многочлена , то произведение меняет знак с минуса на плюс, когда , возрастая, проходит через точку .
4. Последний полином системы не имеет вещественных корней.

Пусть дана конечная упорядоченная система действительных чисел, отличных от нуля, например:

Выпишем знаки этих чисел последовательно:

В системе трижды рядом стоят противоположные знаки. Поэтому говорят, что в упорядоченной системе имеют место три перемены знаков.

Определение 2. Число, равное разности между числом перемен знаков в значениях многочленов ряда Штурма при и при называется характеристикой пары многочленов .

Правило нахождения числа корней многочлена связано с характеристикой пары многочленов и звучит так:

Для того чтобы найти число корней многочлена (не имеющего кратных действительных корней), расположенных между и , надо найти ряд Штурма для многочлена и его производного многочлена и вычислить значения многочленов этого ряда при и при . Разность между числом перемен знаков в первом и втором рядах чисел и будет искомым числом корней.

Это правило является знаменитой теоремой Штурма. [2, с. 19]

Таким образом, для определения числа вещественных корней многочлена , расположенных между и , нужно установить, насколько уменьшается число перемен знаков в системе Штурма данного многочлена при переходе от к .

Для того чтобы воспользоваться теоремой Штурма для нахождения общего числа действительных корней многочлена рассматривают интервал .

Расмотрим применение метода Штурма на примере.

Найдем число корней многочлена и укажем их границы.

Для применения метода Штурма к многочлену требуется составить систему (ряд) Штурма.

Замечание. Многочлен должен иметь действительные корни и не иметь кратных корней.

Правило построения системы Штурма:

1. .
2. Если известны и , то будет равен остатку от деления на , взятым с противоположным знаком: .

Замечание. В процессе деления остаток можно умножать лишь на произвольное положительное число, т. к. знак остатка важен.

Получим систему Штурма:

Определим знаки этих многочленов при и . Для этого достаточно посмтореть на коэффициенты при старших степенях и на сами эти степени.

Занесем результаты выводов в таблицу №1.

Таблица 1.

Знаки многочлена и его производных в бесконечно удаленных точках.

Число перемен знаков

Многочлен имеет действительных корня.

Найдем их границы. Продолжим таблицы, выбрав “на глаз” точки для проверки знаков многочленов системы. Первую точку берем такую, чтобы набор плюсов и минусов был одинаков с , а последующие выгодны такие, при которых количество перемен знаков изменяется, причем таких перемен должно быть ровно столько, сколько корней имеет многочлен.

Таблица 2.

Знаки многочлена и его производных в действительных точках.

Кол-во перемен знаков

Таким образом, система Штурма многочлена теряет по одной перемене знаков при переходе от к и от к . Корни и этого многочлена удовлетворяют, следовательно, неравенствам:

Список литературы:

1. Курош А.Г. Курс высшей алгебры. М.: Наука, 1965. – 431 с.
2. Шафаревич И.Р. О решении уравнений высших степеней (метод Штурма), государственное издательство технико – теоретической литературы. Москва, 1954. – 24 с.

Теоремы Штурма. Краевые задачи

Тема: ТЕОРЕМЫ ШТУРМА. КРАЕВЫЕ ЗАДАЧИ

12.2Понятие о краевых задачах

12.3 Задача Штурма-Лиувилля. Понятие о собственныхчислах и собственных функциях

12.4Решение краевых задач методом функции Грина

12.1 Теоремы Штурма

и рассмотрим два его линейнонезависимые решения и . Мывидим, что между двумя последовательными корнями решения находится один, и только один, кореньрешения . И это не случайно. Любые линейно независимыерешения любого линейного уравнения 2-го порядка, имеющего колебательныерешения, обладает этим свойством.

Т е о р е м а Ш т ур м а. Нули двух действительных линейно независимых решений однородноголинейного уравнения 2-го порядка с действительными коэффициентами взаимноотделяются.

Пусть имеем однородноелинейное уравнение 2-го порядка

линейнонезависимые решения которого обозначим через и . Полагаем . Предположим, что обращаетсяв ноль не менее двух раз на , а и являютсяего двумя последовательными нулями в этом промежутке:

Докажем, что тогда существуетодно, и только одно значение , , для которого . Т.к.функции и линейнонезависимые, то и , ибо впротивном случае

обращался бы в ноль в этих точках. Положим,что совсем не имеет корней на и рассмотрим функцию . Она непрерывна на ,имеет непрерывную производную и обращается в ноль на концах отрезка. Поэтому потеореме Ролля ее производная должна обращаться в ноль хотя бы один раз в интервале, т.е. в т. , , а этоневозможно, т.к.

числитель этой дроби является определителем. В поисках линейнонезависимых решений, т.е. при предположение о том, что совсем не имеет корней на неверно, и функция имеетхотя бы один корень на промежутке .

Их не может быть два,потому что тогда между ними на основании только что доказанного находился быноль функции и, значит, и не были бы последовательными нулями этойфункции, как это предполагалось.

Рассмотренная теорема теряетсилу, если решения недействительные. Так, например, комплексное решение уравнения (12.40) не имеет совсем нулей налюбом промежутке действительной переменной .

В ы в о д из теоремы: еслиодно решение линейного уравнения имеет на промежутке болеедвух нулей, то все решения этого уравнения являются колебательными.

Теорема сравнения

Предыдущая теоремаустанавливает, что решения одного и того же линейного уравнения имеютодинаковый характер (оба колебательные или неколебательные). Естественнопоставить вопрос о сравнении решений двух различных уравнений.

Т е о р е м а. Пустьданы два линейные уравнения 2-го порядка, записанные в самосопряженной форме:

где на. Если на , то решения уравнения (12.43) колеблютсяне медленнее, чем решения уравнения (12.42). Точнее: между двумя корнямирешения (12.42) находится хотя бы один корень каждого решения уравнения(12.43).

Д о к а з а т е л ь с т в о.Пусть и решенияуравнений (12.42) и (12.43) соответственно, т.е.

а и последовательныенули: и на .

Умножив (12.44)на , а (12.45) на и,вычитая почленно, получим:

Интегрируя (12.46) в пределахот до ,находим:

Положим теперь, что не имеет корней на ,тогда на функция однозначна,например .

Не ограничивая общностиположим, что и на . Наосновании наших допущений правая часть равенства (12.47) неотрицательна.Рассмотрим левую часть последнего равенства.

Она отрицательная, т.к. и подопущению, и , т.к. на и и .Равенства и исключаются,т.к. в этом случае . Значит, мы пришли кпротиворечию. Т.о., предположение, что неимеет корней на неверно, т.е. обращается в ноль не меньше одного раза наинтервале . Теорема доказана.

З а м е ч а н и е. Случаи , ; приводятся к рассмотренному случаю и , т.к.наряду с и () и () тожебудут решениями уравнений (12.42) и (12.43).

Если ,то из теоремы следует, что обращается в ноль до появленияочередного нуля функции . Решение , как говорят, осцилирует быстрее,чем .

При применении теоремысравнения в качестве одного из уравнений берут уравнение с постояннымикоэффициентами или такое, которое умеют интегрировать.

П р и м е р. Установитьколичество нулей решения уравнения

Некоторые Теоремы Штурма (стр. 1 из 5)

Быков В.В. bikov@rambler.ru

§1. Предварительные сведения……………………………………5

Тема дипломной работы “Теорема Штурма”, связана с именем французского математика Жака Шарля Франсуа Штурма.

Штурм Жак Шарль Франсуа (Sturm J. Ch. F. – правильное произношение: Стюрм), родился 29 сентября 1803 года в Женеве. Был членом Парижской академии наук с 1836, а также иностранным членом – корреспондентом Петербургской академии наук с того же года. С 1840 года был профессором Политехнической школы в Париже.

Штурм (1824/25) и Раабе (1827) ввели главные формулы сферической тригонометрии при помощи пространственных координат.

Теорему Фурье ( Теорема о числе действительных корней между двумя данными пределами ), математика Жозефа Фурье (Joseph Fourier, 1768-1830), затмила более общая теорема, опубликованная Штурмом в Bull. mathem., 1829.

Доказательство сам Штурм представил только в одной премированной работе 1835г. Коши Огюстен (Cauchy Augustin, 1789-1857) распространил теорему Штурма на комплексные корни (1831). Дополнение к ней дал также Сильвестр Джемс Джозеф (Sylvester Y.Y.

, 1814-1897) в 1839 году и позже.

Основные работы Жана Шарля Штурма относятся к решению краевых задач уравнений математической физики и связанной с этим задачей о разыскивании собственных значений и собственных функций для обыкновенных дифференциальных уравнений. (Задача Штурма-Лиувилля, о нахождении отличных от нуля решений дифференциальных уравнений :

удовлетворяющих граничным условиям вида:

(так называемых собственных функций), а также о нахождении значений параметра l (собственных значений), при которых существуют такие решения. При некоторых условиях на коэффициенты p(t), q(t) задача Штурма-Лиувилля сводилась к рассмотрению аналогичной задачи для уравнения вида: -u¢¢+q(x)u=lu).

Эта задача была впервые исследована Штурмом и Жозефом Лиувиллем (Joseph Liouville, 1809-1882) в 1837г. и закончена в 1841 г.

Также Жак Штурм дал общий метод для определения числа корней алгебраических уравнений, лежащих на заданном отрезке, названный правилом Штурма, который позволяет находить непересекающиеся интервалы, содержащие каждый по одному действительному корню данного алгебраического многочлена с действительными коэффициентами (уже упоминалось выше).

Ему принадлежат ряд работ по оптике и механике.

Штурм Жак Шарль Франсуа умер 18 декабря 1855года.

§ 1. Предварительные сведения

Среди дифференциальных уравнений, наиболее часто исполь­зуемых в математике и физике, следует выделить линейное уравне­ние второго порядка, имеющее вид

Как правило, если не оговорено противное, предполагается, что функции (t), g (f), h (f) и р (f) ¹0, q (t), входящие в эти урав­нения, являются непрерывными (вещественными или комплекс­ными) на некотором t-интервале J, который может быть как огра­ниченным, так и неограниченным. Причина, по которой предпола­гается, что р(t)¹ 0, скоро станет ясной.

Из двух выражений (1.1) и (1.2) последнее является более общим, поскольку уравнение (1.1) может быть записано в виде

если определить p(t) следующим образом:

при некотором a€J. Частичное обращение этого утверждения также верно, поскольку если функция р(t) непрерывно дифференци­руема, уравнение (1.2) можно записать в виде

а это уравнение имеет вид (1.1).

В случае, если функция р (t) непрерывна, но не имеет непрерыв­ной производной, уравнение (1.2) не может быть записано в виде (1.1). Тогда уравнение (1.2) можно интерпретировать как линейную систему из двух уравнений первого порядка для неизвестного двумерного вектора

Другими словами, решение и = и (t) уравнения (1.2) должно быть такой непрерывно дифференцируемой функцией, что функция р(t) u'(t) имеет непрерывную производную, удовлетворяющую (1.2). Если р(t) ¹ 0 и q(t), h(t) непрерывны, к системе (1.

5), а потому и к уравнению (1.2) применимы стандартные теоремы существования и единственности для линейных систем (Мы можем рассматривать также более общие (т. е.

менее гладкие) типы решений, если предполагать, например, только, что функции 1/p(t), q (t), h (t) локально интегрируемы.)

Частному случаю уравнения (1.2) при

принимает вещественные значения, урав­нение (1.2) может быть приведено к такому виду с помощью замены независимых переменных , т.е. (1.7)

при некотором a € J. Функция s = s (t) имеет производную

и потому строго монотонна. Следовательно, функция s = s (t) имеет обратную t= t (s), определенную на некотором s-интервале. После введения новой независимой переменной s урав­нение (1.2) переходит в уравнение (1.8)

где аргумент t выражений p(f)q(t) и p(t) h(f)должен быть заме­нен функцией t = t(s). Уравнение (1.8) является уравнением типа (1.6).

Если функция g (t) имеет непрерывную производную, то урав­нение (1.1) может быть приведено к виду (1.6) с помощью замены неизвестной функции и на z:

при некотором a € J. В самом деле, подстановка (1.9) в (1.1) приводит к уравнению

которое имеет вид (1.6).

В силу сказанного выше, мы можем считать, что рассмат­риваемые уравнения второго порядка в общем случае имеют вид (1.2) или (1.6). Утверждения, содержащиеся в следующих упраж­нениях, будут часто использоваться в дальнейшем.

§ 2. Основные факты

Прежде чем перейти к рассмотрению специальных вопросов, мы получим следствия, касающиеся однородного и неоднородного уравнений

Для этого перепишем скалярные уравнения (2.1) или (2.2) в виде системы двух уравнений

где векторы х= (х1, х2), у == (у1, y2) совпадают с векторами

, , A(t)- матрица второго порядка: (2.5)

Если не оговорено противное, то предполагается, что

, q (t), h (t) и другие коэффициенты являются непрерывными ком­плексными функциями на t-интервале J (который может быть зам­кнутым или незамкнутым, ограниченным или неограниченным).

и , — произвольные комплексные числа, то задача Коши для уравнения (2.2) , (2.6)

имеет единственное решение, существующее при всех

(ii) В частном случае (2.1) уравнения (2.2) и при

соответствующим единственным решением служит функция . Поэтому, если есть решение уравнения (2.1), то нули функции и (t) не могут иметь предельной точки в J.

(iii)Принцип суперпозиции. Если

, —решения урав­нения (2.1), a , -постоянные, то функция является решением уравнения (2.1). Если —решение урав­нения (2.2), то функция также является решением уравнения (2.2) тогда и только тогда, когда функция удовлетворяет уравнению (2.1).

§ О20. Теория осцилляций

§ О20. Теория осцилляций

Новая идея появляется в результате сравнения двух вещей, которые еще не сравнивали.

Теория осцилляций занимается темисвойствами решений уравнения

y′′ +a1(t)y′ +a0(t)y = 0

(1)

и его обобщений, которые можно охарактеризовать словом»колеблемость». Точнее, основной вопрос теории формулируетсятак: как часто у нетривиальных решений уравнения (1)встречаются нули? Эта теория находит важные как математические,так и естественнонаучные приложения (см., в частности,очерк О25).

В дальнейшем мы будем предполагать, что a0 иa1 — непрерывные на всей оси скалярные функции. Слово»решение» всюду ниже будет обозначать лишь нетривиальные решенияуравнения (1).

Первое утверждение в этом направлении, а именно, тот факт, чтолюбое решение уравнения (1) на любом конечноминтервале имеет конечное число нулей, доказывается совсем легко.

Действительно, если на каком-либо конечном промежутке Jнекоторое решение φимеет бесконечное число нулей, скажем t1,t2, …,то в силу компактности промежутка J можно считать, чтоtk →t0 ∈ Jпри k → ∞.

Из равенств φ(tk) = 0(k = 1, 2, …), как легко видеть, следуют равенства

(докажите!). А так как решение любойзадачи Коши дляуравнения (1) единственно,последние равенства гарантируют тривиальность решенияφ. Противоречие.

Таким образом, решение уравнения (1) может иметьбесконечное число нулей только на бесконечном промежутке.В этом случае оно называется осциллирующим,а в противном случае — неосциллирующим.

Фундаментальная роль в теории осцилляций принадлежит формулируемойи доказываемой ниже теореме Штурма. Она позволяет делать заключениеоб осцилляционных свойствах решения уравнения (1),сравнивая это уравнение с уравнениями, осцилляционные свойствакоторых известны.

Прежде чем переходить к формулировке теоремы Штурма сделаемнекоторые упрощающие предположения и преобразования. Пусть вуравнении (1) коэффициент a1непрерывно дифференцируем.

Задача О20.1. Докажите, что после замены переменных

y = xexp ( – 12 ∫ a1(t) dt )

y =x · exp(–1/2∫a1(t)dt)

уравнение (1) преобразуется к виду

Задача О20.2. Докажите, что решениеψ уравнения (2)является осциллирующим в томи только том случае, если решение φ(t) =ψ(t) · exp(–1/2 ∫ a1(t) dt)уравнения (1) является осциллирующим.

Поэтому мы можем считать задачи об осцилляционных свойствахуравнений (1) и (2)эквивалентными. Наряду с уравнением (2)рассмотрим еще одно уравнение такого же вида

с непрерывным коэффициентом b2.

Теорема Штурма.Пусть b1(t) ≤b2(t) при всех t и пустьt1, t2 —последовательные нули решения φуравнения (2). Тогда любое решение ψуравнения (3) имеет на промежутке[t1, t2]хотя бы один нуль (см. рис. 1).

Смысл этой теоремы, если перейти к рассмотрению уравнения малых колебаний маятника(т. е. уравнения гармонических колебаний)

можно выразить словами: частота колебаний более короткого маятника выше.Простейшие возможности теоремыШтурма демонстрируют следующие две задачи.

Задача О20.3. Сравнивая уравнение(2) с самим собой, докажите, что междупоследовательными нулями любого решения φимеется в точности один нуль любого линейно независимогос φ решения. Поэтому нули любых двух решенийуравнения (2) либо совпадают, либо чередуются.

Задача О20.4. Сравнивая уравнение (2) с уравнениемy′′ = 0,докажите, что если b1(t)≤ 0 при всех t,то любое решение уравнения (2) имеет не более одного нуля.

Д о к а з а т е л ь с т в о теоремыШтурма. Предположим противное:решение ψ не имеет нулей на промежутке[t1, t2].Не ограничивая общности, можно считать, что

φ(t) > 0 на(t1, t2) иψ(t) > 0 на[t1, t2]

(иначе мы могли бы рассматривать функции –φ(t)и –ψ(t)). Итак,

Умножив первое тождество на ψ(t),а второе — на φ(t)и вычитая второе из первого, после несложных преобразований получим

ddt [φ′(t)ψ(t)– φ(t)ψ′(t)]= [b2(t) –b1(t)]φ(t)ψ(t).

Поскольку функция φ в точкахt1 и t2обращается в нуль, интегрирование последнего тождества по tв пределах от t1 до t2 приводит к равенству

φ′(t2)ψ(t2) –φ(t1)ψ′(t1) = ∫ [b2(t) –b1(t)]φ(t)ψ(t) dt.

По условию интеграл в правой части равенства неотрицателен. Леваяже часть этого равенства отрицательна. Действительно, из условий

φ(t1) =φ(t2) = 0,φ(t) > 0 при t∈ (t1,t2)

φ′(t1) > 0, аφ′(t2) 0).Тогда уравнение (2) является осциллирующим и,более того, расстояние между соседними нулями любого его решения непревосходит π/ω.Если, дополнительно, при всех t, то расстояние между последовательными нулями любого решения не меньше, чем Доказывается эта теорема сравнением уравнения (2) с уравнениями x′′ +ω2x = 0 и x′′ +Ω2x = 0, решения которых легко выписываются. Сравнение с уравнением приводит к следующему более тонкому утверждению: Теорема.Если при достаточно больших t то уравнение (2) является осциллирующим. Если же при достаточно больших t, то уравнение (2)неосциллирующее. Для д о к а з а т е л ь с т в а достаточнозаметить, что уравнение (4) при α > 1/4имеет общее решение вида x(t) = <C1cos([(4α –1)1/2ln t]/2) +C2sin ([(4α –1)1/2ln t]/2)>t1/2, являющееся осциллирующим, а при α 0, q1(t)≤ q2(t)

при всех t. Тогда между любыми двумя нулямикаждого решения уравнения (6) есть хотя бы один нулькаждого решения уравнения (7).

О20.8. Докажите, что если в уравнении (2)

то это уравнение является осциллирующими, кроме того, расстояние между соседними нулями любого решениястремится к π, когда нули уходят в бесконечность.

О20.9. Пусть в уравнении (2)

Докажите, что это уравнение осциллирующее,причем, если t1, t2, … —занумерованная по возрастанию последовательность (всех) нулей какого-либо решения этогоуравнения, то |tk – tk+1|→ 0 при k → ∞.

О20.10. Пусть в уравнении (2)коэффициент b1 непрерывен на[α, β) иlimt→βb1(t) =+∞. Докажите, что множество нулей любого решенияуравнения (2) образует сходящуюся к βпоследовательность. Покажите, что на любом отрезке [α1,β1] ⊂[α, β)любое решение этого уравнения имеет лишь конечное число нулей.

О20.11. Пусть в уравнении (2)коэффициент b1 монотонно возрастает, аtk — занумерованная по возрастанию последовательностьвсех локальных экстремумов произвольного решения yэтого уравнения. Докажите, что последовательность|y(tk)| монотонно убывает. Еслиже b1 убывает, то |y(tk)| возрастает.

О20.12. Докажите, что если y1 иy2 — решения уравнений (2) и (3)соответственно, такие, что

y1(t0) =y2(t0), y′1(t0)=y′2(t0),

то в условиях теоремы Штурма отношениеy1(t)/y2(t)не убывает от t0 до ближайшего нуля решения y2.

t2y′′ + ty′ +(t2 – ν2)y =0

называется уравнением Бесселя,а его решения — функциями Бесселя. Заменойy√t = z оно приводится к виду

z′′ + ( 1 + 1 – 4ν24t2 ) z = 0.

Докажите, что расстояние между соседними нулями функцииБесселя не превосходит π приν2 ≤ 1/4и не меньше π приν2 ≥ 1/4.Покажите, что уравнение Бесселя являетсяосциллирующим при всех ν.

О20.14. Покажите, что расстояние между соседними нулямифункции Бесселя стремитсяк π при стремлении нулейк +∞.

О20.15. Уравнение (2) называетсяуравнением без сопряженных точекна промежутке J, если любое его решение имеетна J не более одного нуля. Докажите,что уравнение (2)является уравнением без сопряженных точек в том и только томслучае, когда оно имеет строго положительное на J решение.

О20.16. Докажите, что в последней теоремеочерка оценки на b1 можно ослабить до следующих

Источник