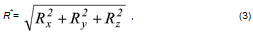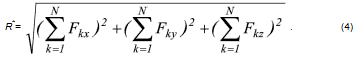Система сходящихся сил равнодействующая системы сходящихся сил способы нахождения равнодействующей

5 Система сходящихся сил. Способы нахождения равнодействующей системы сходящихся сил

§ 3. Система сходящихся сил. Способы нахождения равнодействующей системы сходящихся сил

Система сил, линии действия которых пересекаются в одной точ­ке, называется системой сходящихся сил.

Система сходящихся сил либо приводится к равнодействующей, либо находится в равновесии.

Теорема. Равнодействующая системы сходящихся сил равна век­торной сумме этих сил.

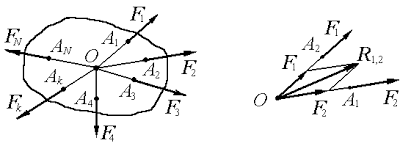
Действительно, пусть к абсолютно твердому телу приложена система сил F_1, F₂, . F_n, линии действия которых пересекаются в некоторой точке О (рис. 9). Мы могли бы складывать последова­тельно эти силы по аксиоме о параллелограмме сил. Однако этот путь очень длинен. Пользуясь правилом геометрического сложения векторов, сразу построим многоугольник сил F₁, F₂, . F_n, замыкающая сторона которого и будет равнодействующей силой R.

Изложенный способ определения равнодействующей является геометрическим. Однако равнодействующую силу R можно определить и аналитически, по проекциям на неподвижные оси декартовой системы координат, выбрав за начало координат точку О пересечения линий действия системы сходящихся сил.

Равновесие системы сходящихся сил.

Рекомендуемые файлы

Условия равновесия системы сходящихся сил

Если система сходящихся сил находится в равновесии, механи­ческим условием равновесия является равенство нулю равнодейст­вующей силы. Получим

Так как векторная сумма сил равна нулю, то многоугольник сил является замкнутым (начало первого вектора силы и конец по­следнего совпадают).

Таким образом, при равновесии системы сходящихся сил много­угольник сил является замкнутым (условие равновесия в геометри­ческой или графической форме).

В аналитической форме условия равновесия системы сходящихся сил заключаются в следующем.

Если пространственная система сходящихся сил находится в рав­новесии, то алгебраическая сумма проекций этих сил на каждую из трех координатных осей должна равняться нулю (на две оси, если система сходящихся сил расположена на плоскости).

Поскольку в случае равновесия указанной системы сил их рав­нодействующая равна нулю (R = 0), то равны нулю и ее проекции на оси координат, т. е. R_х = 0, R_у = 0, R_г = 0. На основании (1.10) получим

Для плоской сходящейся системы сил имеем

Условия (1.13) и (1.14) в аналитической форме называются также уравнениями равновесия. Для статической определенности задачи число неизвестных не должно превышать числа уравнений равно­весия.

Момент силы относительно точки и оси. Главный вектор и главный момент. Пара сил. Момент силы относительно точки

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на силу. Итак, по определению (рис. 12),

Обозначая длину перпендикуляра, опущенного из центра момента на линию действия силы, через h (величину h в дальнейшем будем называть плечом), можно модуль вектора Мо (F) представить в виде произведения Fh, т. е.

Таким образом, момент силы относительно точки — это вектор, направленный перпендикулярно к плоскости, содержащей силу и точку, в ту часть пространства,.

Для аналитического определения момента силы относительно точки выберем произвольную систему координат О_xyz с началом в точке О (рис. 13) и обозначим проекции радиуса-вектора г и силы F на координатные оси О_x, О_Y, О_z, соответственно через х, у, z и X, У, Z. Заметим, что проекции х, у, z радиуса-вектора г точки прило­жения силы одновременно означают координаты этой точки. Тогда, спроектировав обе части векторного равенства (1.15) на оси координат, получим выражение момента силы относительно точки в анали­тической форме в виде трех его проекций на координатные оси:

,

.

Теорема о моменте равнодействующей системы

сходящихся сил (теорема Вариньона)

Момент силы относительно оси

Моментом силы относительно оси называется проекция на ату ось момента силы относительно произвольной точки на оси. Момент силы F относительно оси Оz обозначается через М_z (F). Таким обра­зом,

М

Момент силы относительно оси, как будет показано в динамике, является физической величиной, характеризующей вращательное движение твердого тела.

Согласно определению, моменты силы относительно координат­ных осей выражаются величинами (1.18), т. е. соответственно равны проекциям

М М_У(F) = zХ -хZ; М

Укажем практический способ определения момента силы относи­тельно оси.

Главный вектор и главный момент системы сил

R=

Таким образом, главный вектор системы сил можно определить геометрически с помощью многоугольника сил.

Аналитически главный вектор определяется тремя своими проекциями на координатные оси;

R

R

R

Главным моментом Мо системы сил F_1: F₂, . F_n относительно точки называется векторная сумма моментов этих сил относительно этой точки, т. е

M

Таким образом, главный момент системы сил относительно точки можно определить геометрически с помощью многоугольника момен­тов этих сил относительно данной точки.

Аналитически главный момент относительно точки определяется тремя своими проекциями на координатные оси:

M

M

M

; ;

Заметим, что понятия главного вектора и равнодействующей системы сил не тождественны. Как мы увидим в следующей главе, не всякая система сил имеет равнодействующую. Если же система сил и приводится к равнодействующей, то последняя, хотя геометрически и равна главному вектору, но имеет вполне определенную линию действия, в то время как главный вектор (также и главный момент) является свободным вектором.

В лекции «3. Архитектура операционной системы» также много полезной информации.

Парой сил называется система двух параллельных сил, равных по величине, направленных в противоположные стороны и приложенных к твердому телу.

Пара сил может быть ориентирована положи­тельно (против часовой стрелки в правой системе координат) и отрицательно (по часовой стрелке в левой системе координат). Очевидно, что с переходом от правой системы координат к левой ориентация пары сил изменяется на противоположную. Кратчайшее рас­стояние Н между линиями действия сил пары называется ее плечом.

Главный вектор пары сил равен нулю. Пусть силы F и —F пары приложены соответственно в точках А и В. Определим главный мо­мент пары сил относительно какой-либо точки О. Главный момент пары сил не зависит от выбора центра момен­тов; он обозначается М и называется моментом пары сил:

Итак, момент пары сил — это свободный вектор, по модулю равный М = Fh и направленный перпендикулярно плоскости ее действия так, чтобы с вершины этого вектора пара сил была ориентирована положительно.

Источник

iSopromat.ru

Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Система сходящихся сил

Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, … F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * _1,2 и силы F₃, тогда

Для системы N сил окончательно будем иметь

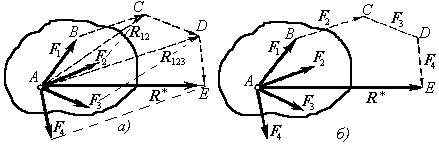
На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.

Силовой многоугольник

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄.

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.

Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

Тогда величина равнодействующей определится следующей формулой:

Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

Здесь α , β , γ — углы между положительным направлением осей координат и равнодействующей.

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник