- Урок 20 Синтез логических выражений §22. Синтез логических выражений
- Содержание урока
- Построение логического выражения Способ 1
- Урок 26 Синтез логических выражений §22. Синтез логических выражений
- Содержание урока
- Построение логического выражения Способ 2
- Урок 26 Синтез логических выражений §22. Синтез логических выражений
- Содержание урока
- Построение логического выражения Способ 1
- Урок 26 Синтез логических выражений §22. Синтез логических выражений
- Содержание урока
- Построение логического выражения Способ 3
- Урок 20 Синтез логических выражений §22. Синтез логических выражений
- Содержание урока
- Построение логического выражения Способ 2
Урок 20
Синтез логических выражений
§22. Синтез логических выражений
Содержание урока
Построение логического выражения. Способ 1
Построение логического выражения
Способ 1
До этого момента мы считали, что логическое выражение уже задано и нам надо что-то с ним сделать (построить таблицу истинности, упростить и т. п.). Такие задачи называются задачами анализа (от греческого — разложение), в них требуется исследовать заданное выражение. При проектировании различных логических устройств, в том числе и устройств компьютеров, приходится решать обратную задачу — строить логическое выражение по готовой таблице истинности, которая описывает нужное правило обработки данных. Эта задача называется задачей синтеза (от греческого — совмещение).
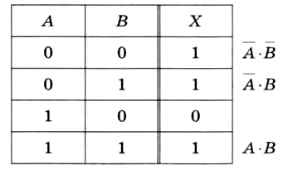
В качестве простейшего примера построим логическое выражение, тождественное операции импликации X = А —> В, по её таблице истинности (рис. 3.19).

Например, выражение А • B истинно только при А = 0 и В = 0, т. е. только в первой строке таблицы. Выражение А • В истинно только во второй строке, а А • В — только в последней.
Существует простое правило: если в некоторой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания.
Складывая выражения для всех отмеченных строк (кроме третьей, где функция равна нулю), получаем:
Х = А • B + А • В + А • В.
Упрощаем это выражение:
X = А • ( B + В) + А • В = А + А • В = ( А + А) • ( А + В) = А + В.
Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции «НЕ» и «ИЛИ».
Следующая страница 
Cкачать материалы урока
Источник
Урок 26
Синтез логических выражений
§22. Синтез логических выражений
Содержание урока
Построение логического выражения. Способ 2
Построение логического выражения
Способ 2

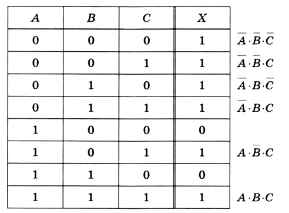
Рассмотрим более сложный пример, когда выражение зависит от трёх переменных. В этом случае в таблице истинности будет 8 строк (рис. 3.20).
Отметим все строки, где X = 1, и для каждой из них построим выражение, истинное только для этой комбинации переменных (см. рис. 3.20). Теперь выполним логическое сложение:
Х = А • B • C + А • B • C + А • B • C + А • B • C + А • B • C + А • B • C.
Упрощение этого выражения даёт:
X = А • B • ( C + С) + А • В ( C + С) + А • С • ( B + В) = А • B + А • B + А • С = А • ( B + В) + А • С = А + А • С = ( А + А) • ( А +С) = А + С.
Используя второй способ, получаем:
X = А • B • ( C + А • В • C = А • C • ( B + В) = А • C .
Тогда X = А • C = А + С. В данном случае второй способ оказался проще, потому что в столбце X таблицы истинности меньше нулей, чем единиц.
Следующая страница 
Cкачать материалы урока
Источник
Урок 26
Синтез логических выражений
§22. Синтез логических выражений
Содержание урока
Построение логического выражения. Способ 1
Построение логического выражения
Способ 1
До этого момента мы считали, что логическое выражение уже задано и нам надо что-то с ним сделать (построить таблицу истинности, упростить и т. п.). Такие задачи называются задачами анализа (от греческого — разложение), в них требуется исследовать заданное выражение. При проектировании различных логических устройств, в том числе и устройств компьютеров, приходится решать обратную задачу — строить логическое выражение по готовой таблице истинности, которая описывает нужное правило обработки данных. Эта задача называется задачей синтеза (от греческого — совмещение).
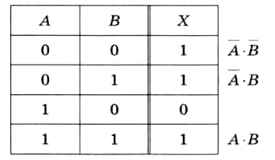
В качестве простейшего примера построим логическое выражение, тождественное операции импликации X = А —> В, по её таблице истинности (рис. 3.19).

Например, выражение А • B истинно только при А = 0 и В = 0, т. е. только в первой строке таблицы. Выражение А • В истинно только во второй строке, а А • В — только в последней.
Существует простое правило: если в некоторой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания.
Складывая выражения для всех отмеченных строк (кроме третьей, где функция равна нулю), получаем:
Х = А • B + А • В + А • В.
Упрощаем это выражение:
X = А • ( B + В) + А • В = А + А • В = ( А + А) • ( А + В) = А + В.
Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции «НЕ» и «ИЛИ».
Следующая страница 
Cкачать материалы урока
Источник
Урок 26
Синтез логических выражений
§22. Синтез логических выражений
Содержание урока
Построение логического выражения. Способ 3
Построение логического выражения
Способ 3

X = А • B • C + A • B • C
Применяя закон де Моргана, получим:
X = (А • B • C ) + (A • B • C ) .
Используя закон де Моргана для обеих скобок, находим:
X =( А + В + С) • ( А + B + С).
Заметим, что выражение в каждой скобке ложно только для одной комбинации исходных данных, при которых Х = 0.
Таким образом, третий способ заключается в том, чтобы для каждой строки в таблице истинности, где выражение равно 0, построить логическую сумму, в которую переменные, равные в этой строке единице, входят с инверсией, а равные нулю — без инверсии. Выражение для X — это произведение полученных сумм.
В нашем примере выражение упрощается с помощью распределительного закона для «И» и закона исключённого третьего:
Х = ( А + В + С) • ( А + В + С) = ( А + С) + В • B = А + С.
Неудивительно, что мы получили тот же ответ, что и раньше.
Иногда при упрощении выражений может потребоваться искусственный приём, который сначала вроде бы усложняет запись, но затем позволяет получить более простую форму. Например, рассмотрим выражение
Х = А • В + А • С + B • С.
Учитывая, что В + B = 1, можно представить второе слагаемое в виде:
А • С = А • (В + B ) • С = А • В • С + ( А • ( B • С.
Х = А • В + А • В • С + B • С = А • В • (1 + С)+ ( А + 1) • В • С = А • В + В • С.
Подготовьте сообщение
а) «Совершенные нормальные формы»
Следующая страница 
Cкачать материалы урока
Источник
Урок 20
Синтез логических выражений
§22. Синтез логических выражений
Содержание урока
Построение логического выражения. Способ 2
Построение логического выражения
Способ 2

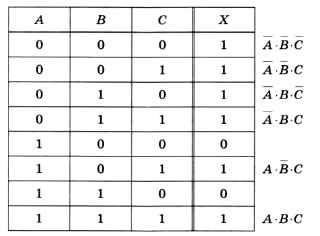
Рассмотрим более сложный пример, когда выражение зависит от трёх переменных. В этом случае в таблице истинности будет 8 строк (рис. 3.20).
Отметим все строки, где X = 1, и для каждой из них построим выражение, истинное только для этой комбинации переменных (см. рис. 3.20). Теперь выполним логическое сложение:
Х = А • B • C + А • B • C + А • B • C + А • B • C + А • B • C + А • B • C.
Упрощение этого выражения даёт:
X = А • B • ( C + С) + А • В ( C + С) + А • С • ( B + В) = А • B + А • B + А • С = А • ( B + В) + А • С = А + А • С = ( А + А) • ( А +С) = А + С.
Используя второй способ, получаем:
X = А • B • ( C + А • В • C = А • C • ( B + В) = А • C .
Тогда X = А • C = А + С. В данном случае второй способ оказался проще, потому что в столбце X таблицы истинности меньше нулей, чем единиц.
Следующая страница 
Cкачать материалы урока
Источник