Синтез логических выражений 10 класс 3 способ

Урок 26
Синтез логических выражений
§22. Синтез логических выражений

Содержание урока

Построение логического выражения. Способ 3

Построение логического выражения
Способ 3

Способ 3. При небольшом количестве нулей можно использовать ещё один метод. Попробуем применить операцию «НЕ» к исходному выражению для X, без предварительного упрощения:

X = А • B • C + A • B • C

Применяя закон де Моргана, получим:

X = (А • B • C ) + (A • B • C ) .

Используя закон де Моргана для обеих скобок, находим:

X =( А + В + С) • ( А + B + С).

Заметим, что выражение в каждой скобке ложно только для одной комбинации исходных данных, при которых Х = 0.

Таким образом, третий способ заключается в том, чтобы для каждой строки в таблице истинности, где выражение равно 0, построить логическую сумму, в которую переменные, равные в этой строке единице, входят с инверсией, а равные нулю — без инверсии. Выражение для X — это произведение полученных сумм.

В нашем примере выражение упрощается с помощью распределительного закона для «И» и закона исключённого третьего:

Х = ( А + В + С) • ( А + В + С) = ( А + С) + В • B = А + С.

Неудивительно, что мы получили тот же ответ, что и раньше.

Иногда при упрощении выражений может потребоваться искусственный приём, который сначала вроде бы усложняет запись, но затем позволяет получить более простую форму. Например, рассмотрим выражение

Х = А • В + А • С + B • С.

Учитывая, что В + B = 1, можно представить второе слагаемое в виде:

А • С = А • (В + B ) • С = А • В • С + ( А • ( B • С.

Х = А • В + А • В • С + B • С = А • В • (1 + С)+ ( А + 1) • В • С = А • В + В • С.

Подготовьте сообщение

а) «Совершенные нормальные формы»

Следующая страница Задачи

Cкачать материалы урока

Источник

Урок 20
Синтез логических выражений
§22. Синтез логических выражений

Содержание урока

Построение логического выражения. Способ 3

Построение логического выражения
Способ 3

Способ 3. При небольшом количестве нулей можно использовать ещё один метод. Попробуем применить операцию «НЕ» к исходному выражению для X, без предварительного упрощения:

X = А • B • C + A • B • C

Применяя закон де Моргана, получим:

X = (А • B • C ) + (A • B • C ) .

Используя закон де Моргана для обеих скобок, находим:

X =( А + В + С) • ( А + B + С).

Заметим, что выражение в каждой скобке ложно только для одной комбинации исходных данных, при которых Х = 0.

Таким образом, третий способ заключается в том, чтобы для каждой строки в таблице истинности, где выражение равно 0, построить логическую сумму, в которую переменные, равные в этой строке единице, входят с инверсией, а равные нулю — без инверсии. Выражение для X — это произведение полученных сумм.

В нашем примере выражение упрощается с помощью распределительного закона для «И» и закона исключённого третьего:

Х = ( А + В + С) • ( А + В + С) = ( А + С) + В • B = А + С.

Неудивительно, что мы получили тот же ответ, что и раньше.

Иногда при упрощении выражений может потребоваться искусственный приём, который сначала вроде бы усложняет запись, но затем позволяет получить более простую форму. Например, рассмотрим выражение

Х = А • В + А • С + B • С.

Учитывая, что В + B = 1, можно представить второе слагаемое в виде:

А • С = А • (В + B ) • С = А • В • С + ( А • ( B • С.

Х = А • В + А • В • С + B • С = А • В • (1 + С)+ ( А + 1) • В • С = А • В + В • С.

Подготовьте сообщение

а) «Совершенные нормальные формы»

Следующая страница Задачи

Cкачать материалы урока

Источник

Синтез логических выражений Поверина

Тема урока «Синтез логических выражений» (урок информатики в 10 классе информационно-технологического профиля)

Учитель Поверина Ирина Александровна

МОУ «СОШ п. Знаменский Ивантеевского района Саратовской области»

Содержание

Организационный момент [ править ]

Приветственное слово учителя. [ править ]

Сделать в жизни важный шаг — это, братцы, не пустяк!

Всё надо тщательно продумать, посмотреть и так, и сяк.

Посоветоваться с мамой, у отца совет спросить,

Вспомнить: «Я — десятиклассник!», свою логику включить.

Сразу ты, дружок, поймёшь, что есть ИСТИНА, что — ЛОЖЬ.

У компьютера внутри тоже логика. Смотри!

Определение задач урока. [ править ]

Учитель:Мы с вами изучили достаточно большой блок материала из раздела «Логика». Как вы думаете, какие задачи мы можем обозначить для первой части урока?

1. Применение на практике полученных знаний
2. Развитие логического мышления
3. Формирование информационной культуры

Правила заполнения Карты индивидуальных достижений. [ править ]

Учитель: На столах для вас приготовлены карточки-задания. Результаты выполнения необходимо занести в Карту индивидуальных достижений. В конце урока вы сами оцените свою работу по имеющимся критериям.

Актуализация опорных знаний. [ править ]

Основные логические операции [ править ]

Учитель: Давайте вместе вспомним формулы и запишем таблицы истинности основных логических операций.

Учащиеся: пятеро учащихся выходят к доске и заполняют таблицу, остальные — делают записи в тетрадях.

Основные логические элементы [ править ]

Учитель: Установить соответствие между названиями логических элементов и изображениями.

Ученик: на доске соединяет линиями соответствующие элементы.

Построение таблицы истинности сложного выражения [ править ]

Учитель: Составим таблицу истинности для сложного выражения F=A&B \/ B&C \/ A&C

Учащиеся: заполняют таблицу на доске и делают записи в тетрадях.

Учитель:Таблицу истинности можно построить и с помощью электронных таблиц Microsoft Office Excel. (Слайды 9, 10, 11)

Проблемная ситуация [ править ]

А если наоборот задачу поставить:

Как по таблице истинности функцию составить?

Тема урока: «Синтез логических выражений».

Цель: Сегодня мы будем учиться составлять логические функции по таблицам истинности и строить логическую схему в Конструкторе

Объяснение нового материала. [ править ]

(Слайды 13, 14, 15, 16)

(При демонстрации слайдов можно использовать функцию доски «затемнение экрана» для постепенного погружения учащихся в материал)

Учитель: Синтезировать (составить) логическое выражение по таблице истинности можно двумя способами:

Шаг 1. Отметить строки в таблице, где F = 1.

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат.

Шаг 1. Отметить строки в таблице, где F = 0.

Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.

Шаг 3. Сложить эти выражения и упростить результат.

Шаг 4. Сделать инверсию полученного выражения.

(Алгоритм желательно повторить учащимся самостоятельно с помощью учителя)

Построение логического выражения по таблице истинности [ править ]

Учитель: Предлагаю выполнить задание, применив законы алгебры логики.

Учащиеся: Выполняют работу в тетради и на доске.

Знакомство с «Конструктором логических схем» [ править ]

Учитель знакомит учащихся с новым программным продуктом.

Предлагаю услуги инструктора по освоению нового конструктора. Он доступен, прост, понятен всем и помогает в построении логических схем.

Здесь есть элементы простые и сложные, и провода – соединения всевозможные. По логической функции схему построим. Для этого режим «Редактор» откроем. Нужные блоки на сетку поместим и проводами все соединим.

В режим «Контроль» без промедления входим, и тестирование схемы проводим: На входы полный набор значений подаем и выходные сигналы узнаем. Таблицу истинности в тетради сохраним и, если есть, вопросы зададим.

Учитель, используя интерактивную доску, демонстрирует работу в Конструкторе на примере простого логического выражения F=A&B (повторяет алгоритм работы в программе, показывает все режимы работы Конструктора — редактор и контроль) и отвечает на вопросы учащихся.

Конструктор логических схем для Windows Версия 1.11

Физкультурная минутка [ править ]

Выполнение упражнений под веселую музыку.

Формирование умений и навыков. [ править ]

Составление таблицы истинности в редакторе электронных таблиц [ править ]

Задание №1(на карточке)

Синтез логического выражения [ править ]

Самостоятельная работа (на карточке)

Работа с Конструктором [ править ]

Построить логическую схему по полученному выражению и провести ее тестирование (ввести полный набор значений входных сигналов и записать выходные сигналы)

Тестирование [ править ]

Итог урока. [ править ]

Учитель: Чем я вас сегодня удивила? Что нового узнали? Что не поняли?

• Запись домашнего задания (Слайд 22)
• Выставление отметок.

Учитель:Посмотрите, пожалуйста, на свои Карты индивидуальных достижений. Отметку «отлично» получает тот, у кого совпадают записи логических выражений и таблицы истинности в двух первых заданиях. Дополнительные бонусные баллы получают ученики, прошедшие тестирование.

Учитель: Всем большое спасибо. До свидания

Источник

Урок 26
Синтез логических выражений
§22. Синтез логических выражений

Содержание урока

Построение логического выражения. Способ 2

Построение логического выражения
Способ 2

Способ 2. Если в таблице истинности нулей меньше, чем единиц, удобнее сначала найти формулу для обратного выражения, X , а потом применить операцию «НЕ». В данном случае выражение равно нулю в единственной строке, при А =1 и В =0, только в этой строке X = 1, поэтому, используя предыдущий способ, получаем X = А • В. Теперь остаётся применить операцию «НЕ» и закон де Моргана:

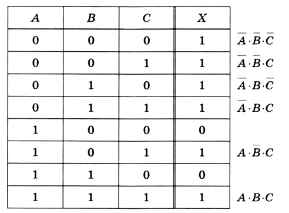
Рассмотрим более сложный пример, когда выражение зависит от трёх переменных. В этом случае в таблице истинности будет 8 строк (рис. 3.20).

Отметим все строки, где X = 1, и для каждой из них построим выражение, истинное только для этой комбинации переменных (см. рис. 3.20). Теперь выполним логическое сложение:

Х = А • B • C + А • B • C + А • B • C + А • B • C + А • B • C + А • B • C.

Упрощение этого выражения даёт:

X = А • B • ( C + С) + А • В ( C + С) + А • С • ( B + В) = А • B + А • B + А • С = А • ( B + В) + А • С = А + А • С = ( А + А) • ( А +С) = А + С.

Используя второй способ, получаем:

X = А • B • ( C + А • В • C = А • C • ( B + В) = А • C .

Тогда X = А • C = А + С. В данном случае второй способ оказался проще, потому что в столбце X таблицы истинности меньше нулей, чем единиц.

Следующая страница Построение логического выражения. Способ 3

Cкачать материалы урока

Источник

Урок 26
Синтез логических выражений
§22. Синтез логических выражений

Содержание урока

Построение логического выражения. Способ 1

Построение логического выражения
Способ 1

До этого момента мы считали, что логическое выражение уже задано и нам надо что-то с ним сделать (построить таблицу истинности, упростить и т. п.). Такие задачи называются задачами анализа (от греческого — разложение), в них требуется исследовать заданное выражение. При проектировании различных логических устройств, в том числе и устройств компьютеров, приходится решать обратную задачу — строить логическое выражение по готовой таблице истинности, которая описывает нужное правило обработки данных. Эта задача называется задачей синтеза (от греческого — совмещение).

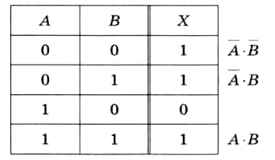
В качестве простейшего примера построим логическое выражение, тождественное операции импликации X = А —> В, по её таблице истинности (рис. 3.19).

Способ 1. В таблице истинности мы выделяем все строки, где логическое выражение равно единице. Тогда искомое выражение может быть записано как логическая сумма выражений, каждое из которых истинно только^ одном случае.

Например, выражение А • B истинно только при А = 0 и В = 0, т. е. только в первой строке таблицы. Выражение А • В истинно только во второй строке, а А • В — только в последней.

Существует простое правило: если в некоторой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания.

Складывая выражения для всех отмеченных строк (кроме третьей, где функция равна нулю), получаем:

Х = А • B + А • В + А • В.

Упрощаем это выражение:

X = А • ( B + В) + А • В = А + А • В = ( А + А) • ( А + В) = А + В.

Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции «НЕ» и «ИЛИ».

Следующая страница Построение логического выражения. Способ 2

Cкачать материалы урока

Источник