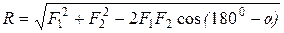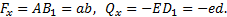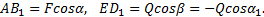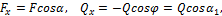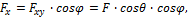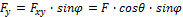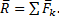Геометрический способ сложения сходящихся сил
Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке. Две силы, сходящиеся в одной точке, согласно третьей аксиоме статики можно заменить одной силой – равнодействующей.
Решение многих задач статики связано с операцией сложения векторов, в частности, сил.
Главный вектор системы сил – величина, равная геометрической сумме сил системы. Главный вектор системы сил не следует путать с равнодействующей. Равнодействующая – всегда главный вектор, а главный вектор равен равнодействующей, если система сил является сходящейся.
Равнодействующую плоской системы сходящихся сил можно определить графически и графоаналитически.
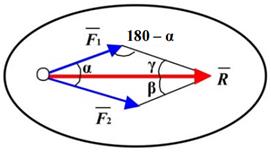
Сложение двух сил. При графическом определении равнодействующей на чертеже и выбранном масштабе изображаются силы, затем они складываются по правилу параллелограмма. По длине диагонали параллелограмма, учитывая выбранный масштаб, определяется равнодействующая, равная сумме слагаемых сил. Точность определения равнодействующей зависит в этом случае от точности построения силового треугольника.
Графоаналитический способ сложения сил позволяет более точно определить равнодействующую, используя тригонометрические зависимости:
или 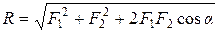
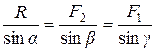
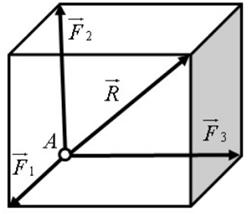
Сложение трех сил, не лежащих в одной плоскости: геометрическую сумму 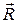
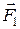
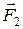
 |  |
| Рис. 1.19 | Рис. 1.20 |
Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис.1.21), либо путём построения силового многоугольника (рис.1.22).
Источник
Геометрический способ сложения сил
Сложение сил.
Система сходящихся сил
Главным вектором системы сил называют геометрическую сумму сил системы.
Сложение двух сил. Геометрическая сумма 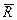
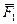
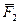
Модуль равнодействующей силы
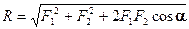 . . | (1.3) |
где α – угол между силами.
Углы, которые сила образует со слагаемыми силами, определяются из уравнения
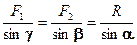 . . | (1.4) |
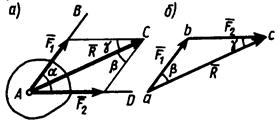
Рисунок 1.15 – Сложение двух сил: а – по правилу параллелограмма; б – построением силового треугольника
Сложение трёх сил, не лежащих в одной плоскости. Геометрическая сумма 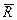
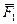
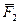
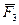
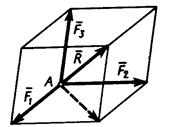 | Рисунок 1.16 – Сложение трёх сил, не лежащих в одной плоскости |
Сложение системы сил.Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 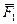
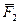
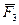
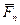
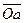
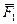
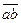
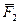
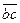
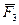
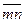
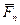
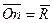
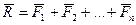 или или 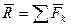 . . | (1.5) |
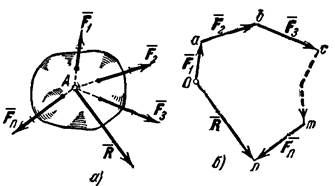
 | Рисунок 1.17 – Система сходящихся сил и её геометрическая сумма (главный вектор) 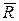 , являющийся равнодействующей , являющийся равнодействующей |
Равнодействующая сходящихся сил,т.е. сил, линии действия которых пересекаются в одной точке (рис. 1.17, а).
Т.к. сила, действующая на абсолютно твёрдое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке (на рис. 1.17, а в точке А). Последовательно применяя закон параллелограмма сил, придём к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. Следовательно, система сил 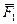
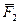
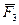
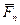
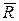
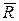
В задачах механики система сходящихся сил может быть приложена к материальной точке массой m, тогда равнодействующая сила 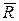
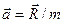
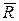

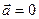
Все силы, приложенные к точке, являются сходящимися, поэтому собственное вращение материальной точки не рассматривается. Чтобы изменить вращение твёрдого тела, к нему надо приложить не сходящуюся систему сил. Если на твёрдое тело действует только сходящаяся система сил, то состояние вращения твёрдого тела не изменяется.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Геометрический способ сложения сил.
Проекция силы на ось и на плоскость.
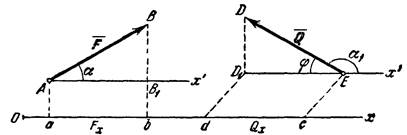
Перейдем к рассмотрению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус — если в отрицательном. Из определения следует, что проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу. Этим удобно пользоваться при вычислении проекции силы на ось, не лежащую в одной плоскости с силой.
Рис. 1
Обозначать проекцию силы 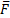
Но из чертежа видно, что
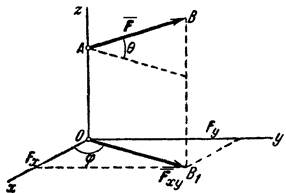
т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси — острый, и отрицательной, если этот угол — тупой; если сила перпендикулярна к оси, то ее проекция на ось равна нулю.
Рис.2
Проекцией силы 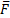
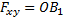
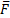
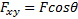
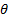
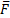
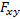
В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроектировать на данную ось.
Например, в случае, изображенном на рис. 2, найдем таким способом, что
Геометрический способ сложения сил.
Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.
Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 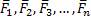
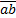
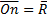
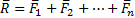
От порядка, в котором будут откладываться векторы сил, модуль и направление 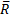
Рис.3
Фигура, построенная на рис. 3,б, называется силовым (в общем случае векторным) многоугольником. Таким образом, геометрическая сумма или главный вектор нескольких сил изображается замыкающей стороной силового многоугольника, построенного из этих сил (правило силового многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора 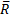
Равнодействующая сходящихся сил. При изучении статики мы будем последовательно переходить от рассмотрения более простых систем сил к более сложным. Начнем с рассмотрения системы сходящихся сил.
Сходящимися называются силы, линии действия которых пересекаются в одной точке, называемой центром системы (см. рис. 3, а).
По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 3, а в точке А).
Последовательно применяя аксиому параллелограмма сил, приходим к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы 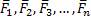
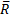
1. Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник — отличный от первого.
2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.
3. Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.
Источник