Сила тяжести способы изменения

Изменение силы тяжести

Изменение силы тяжести с широтой места и высотой над поверхностью Земли

Причина тяжести тел (их весомости) – действие на них сил тяготения Земли.

Если бы Земля была шаром и не вращалась вокруг своей оси, то сила тяжести на Земле была бы равна силе тяготения: F = ? · mM / R 2

Но Земля несколько сплюснута у полюсов: полярный радиус её меньше экваториального примерно на 21 км. Главная же причина изменения силы тяжести – вращение Земли вокруг своей оси.

При вращении Земли линейные скорости точек, лежащих на разных широтах, различны: на полюсах линейная скорость равна нулю» а на экваторе она наибольшая. Поэтому силы, обеспечивающие круговое движение точек Земли, на разных широтах различны. Центростремительной силой в данном случае служит составляющая силы тяготении.

На рисунке схематически изображены различные положения тела с массой т на поверхности Земли: в средних широтах, на полюсе и на экваторе. Вектор F – сила тяготения, с которой покоящееся (относительно Земли) тело притягивается Землёй.

Так как тело вращается вместе с Землей, то на него действует центростремительная сила F_ц.с., которую можно представить как одну из составляющих силы тяготения F. Величина центростремительной силы может быть вычислена во формуле:

F_ц.с. = m? 2 r или F_ц.с. = m? 2 Rcos?

Где ? – угловая скорость вращения Земли, r – радиус параллельного круга, R – радиус Земли, ? – широта точки.

Другую составляющую силы тяготения – силу Р – называют силой тяжести. Направление силы тяжести называют отвесным, оно, как видно из чертежа, только на полюсах и экваторе совпадает с радиусом Земли.

Наблюдатель, находящийся на поверхности Земли и, следовательно, участвующий в её суточном вращении, будет наблюдать действие лишь одной составляющей — силы тяжести Р.

Действие силы тяжести Р проявляется двояко; динамически — в сообщении телам ускорения (Р = mg) и статически — в давлении на опору или в натяжении подвеса.

На полюсах линейная скорость вращения точек Земли равна нулю, следовательно, равна нулю и центростремительная сила (F_ц.с.), поэтому на полюсах сила тяжести равна силе тяготения:

Р_полюс = F = ? · mM / R 2

На экваторе центростремительная сила F_ц.с. направлена, как и сила тяготения F, по радиусу к центру Земли, поэтому сила тяжести на экваторе:

Р_{экватор} = F – F_ц.с. = F – m? 2 R

На любой другой широте ? сила тяжести меньше силы тяготения на величину составляющей центростремительной силы (f), направленной вдоль радиуса Земли.

P? = ? · mM / R 2 — m? 2 Rcos 2 ?

Из формулы Р = mg следует, что ускорение силы тяжести g изменяется с изменением широты места. На полюсе g_п = 9,83 м/сек 2 ; на экваторе g_э = 9,78 м/сек 2 . Ускорение силы тяжести на широте 45° и на уровне моря называют нормальным, оно равно 9,80665 м/сек 2 .

С высотой над поверхностью Земли сила тяжести убывает, что видно из формулы закона тяготения:

F = ? · mM / (R + h) 2

где h — высота относительно поверхности Земли.

Источник

Сила тяжести, масса и вес тела, невесомость

Масса

Масса обозначается символом \(m \), является скалярной величиной и в СИ измеряется в килограммах.

Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:

\[ \large \boxed < \beginm = \left( \text <тонны>\right) \cdot 10^ <3>\left( \text<кг>\right) \\ m = \left( \text <центнеры>\right) \cdot 10^ <2>\left( \text<кг>\right) \\ m = \left( \text <граммы>\right) \cdot 10^ <-3>\left( \text<кг>\right) \\ m = \left( \text <миллиграммы>\right) \cdot 10^ <-6>\left( \text<кг>\right) \\ \end> \]

• \( \large \text <(тонны)>\) – подставьте количество тонн вместо этой скобки;
• \( \large \text <(центнеры)>\) – вместо этой скобки подставьте количество сотен килограммов;
• \( \large \text <(граммы)>\) – подставьте количество граммов вместо этой скобки;
• \( \large \text <(миллиграммы)>\) – вместо этой скобки подставьте количество миллиграммов;

От массы зависят инерционные и гравитационные свойства физических тел.

Масса в природе проявляет себя двумя способами. Поэтому, выделяют:

1. массу инертную и
2. массу гравитационную.

Инертная масса

Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.

Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».

Гравитационная масса

Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.

Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.

Так же, масса входит в формулы для расчета импульса и механической энергии.

Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.

Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.

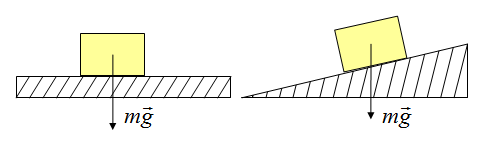
Сила тяжести

Сила тяжести — это сила, с которой Земля притягивает к себе тело.

\(\large \vec>> \left(H\right) \) — сила тяжести, она действует на тело со стороны планеты (или другого крупного небесного тела, например, астероида, или звезды).

\(\large m \left(\text<кг>\right) \) — масса тела;

\(\large \vec \left(\frac<\text<м>>>\right) \) — ускорение свободного падения, это не постоянная величина, она может меняться. Читайте подробнее о ускорении свободного падения .

Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.

Является векторной величиной и обозначается символом \(\vec

\).

\(\vec

\left(H\right) \) – вес тела, как любая сила в СИ измеряется в Ньютонах.

Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.

Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу \(\large \vec\). Как только мы найдем реакцию опоры \(\large \vec\), мы найдем вес тела, давящего на эту опору.

Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.

Чем вес отличается от силы тяжести

Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.

Что такое невесомость

Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.

Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.

Как изменяется вес тела лифте

Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.

Если скорость лифта не изменяется

Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.

Примечание: «неизменной», также, значит «постоянной», или «одной и той же».

По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.

Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.

Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:

\[ \large N – m \cdot g = 0 \]

А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).

Прибавив к обеим частям уравнения величину \( m \cdot \vec \), получим

\[ \large N = m \cdot g \]

По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.

Воспользуемся тем, что \( \left|\vec \right|= \left|\vec

\right|\), получим

То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен \( mg \). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета.

Если скорость лифта изменяется

Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2).

Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах.

Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так:

\[ \large N – m \cdot g = m \cdot a \]

А для рисунка 2б, так:

\[ \large N – m \cdot g = — m \cdot a \]

Прибавим теперь к обеим частям уравнений величину \( m \cdot g \), получим:

\( \large N = m \cdot a + m \cdot g \) – для случая рис. 2а;

\( \large N = — m \cdot a + m \cdot g \) – для рис. 2б;

Вынесем массу за скобки

\( \large N = m \cdot \left( a + g \right) \) – для рис. 2а;

\( \large N = m \cdot \left( -a + g \right) \) – для рис. 2б;

Учтем, что \( \left|\vec \right|= \left|\vec

\right|\), окончательно запишем

Для рисунка 2а — движение лифта вверх с ускорением:

Вес тела в движущемся с ускорением вверх лифте, будет равен \( m \cdot \left( g + a \right) \), то есть, превышает величину \( m \cdot g \).

Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается:

Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен \( m \cdot g \).

Вес тела в движущемся вниз с ускорением лифте, равен \( m \cdot \left( g — a \right) \), это меньше величины \( m \cdot g \).

Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать!

Что такое перегрузка

Когда вес тела больше силы тяжести, говорят, что возникает перегрузка.

\[ \large \boxed < P >m \cdot g >\]

Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения \(\large \vec\).

Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз.

Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…».

Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить.

Подведем итоги

\(P = m \cdot g \) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте.

\( P = m \cdot \left( g + a \right) \) — вес, когда лифт движется с ускорением вверх;

\( P = m \cdot \left( g — a \right) \) — вес в движущемся вниз с ускорением;

Если ускорение лифта при его движении вниз \( a = g \), наступит невесомость, вес тела исчезнет \( P = 0 \).

Источник

Сила тяжести способы изменения

В данном параграфе мы напомним Вам о силе тяжести, центростримительном ускорение и весе тела

На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.

Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести

где М — масса Земли; R — радиус Земли.
Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле F т =GMm/R 2 модуль ускорения свободного падения g находят по формуле

Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде

В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы F т =GMm/R 2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.

Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют связями. Под действием силы тяжести связи деформируются и сила реакции деформированной связи по третьему закону Ньютона уравновешивает силу тяжести.

На ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета — Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.

Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с 2 .

Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле

Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2.
Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.

Вес тела. Невесомость и перегрузки

Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес — это упругая сила, приложенная к опоре или подвесу (т. е. к связи).

Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести F_т только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае

Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.

Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести F_т=mg и сила упругости F_yп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил F_т и F_уп дает равнодействующую, вызывающую ускорение тела, т. е.

Согласно приведенному выше определению понятия «вес», можно написать, что Р=-F_yп. Из формулы: F т + F уп =mа. с учетом того, что F т =mg, следует, что mg-mа=-F yп . Следовательно, Р=m(g-а).

Силы F_т и F_уп направлены по одной вертикальной прямой. Поэтому если ускорение тела а направлено вниз (т.е. совпадает по направлению с ускорением свободного падения g), то по модулю

Если же ускорение тела направлено вверх (т. е. противоположно направлению ускорения свободного падения), то

Следовательно, вес тела, ускорение которого совпадает по направлению с ускорением свободного падения, меньше веса покоящегося тела, а вес тела, ускорение которого противоположно направлению ускорения свободного падения, больше веса покоящегося тела. Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.

При свободном падении a=g. Из формулы: P=m(g-a)

следует, что в таком случае Р=0, т. е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости. Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.

Источник