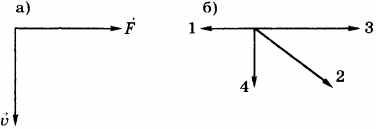Сила. Сложение сил
1. Ускорения взаимодействующих тел обратно пропорциональны их массам: \( \frac
Силой называют физическую величину, характеризующую взаимодействие тел и равную произведению массы тела и его ускорения. Поскольку ускорение векторная величина, а масса скалярная, то сила — векторная величина: \( \vec
2. Единица силы, в отличие от единицы массы, является производной единицей СИ. \( [\,F\,]=[\,m\,][\,a\,] \) ; \( [\,F\,] \) = 1кг · 1 м/с 2 . \( [\,F\,] \) = 1 Н (1 ньютон).
Один ньютон — это такая сила, которая телу массой 1 кг сообщает ускорение 1 м/с 2 .
3. Результат действия силы зависит от её модуля, направления и точки приложения. Например, дверную ручку прикрепляют как можно дальше от петель, на которых она висит, поскольку, чем ближе к петлям подействовать силой, тем труднее дверь открыть.
4. Прибором для измерения силы служит динамометр. В соответствии с законом Гука удлинение пружины прямо пропорционально силе упругости, поэтому по удлинению пружины можно судить о приложенной к пружине силе, которая равна силе упругости.
5. Обычно на тело действуют несколько сил. Например, на тело, падающее в воздухе, действуют сила тяжести и сила сопротивления воздуха; на груз, висящий на нити, действуют сила тяжести и сила упругости нити.
При этом действие каждой силы не зависит от действия других, т.е. каждая сила сообщает телу такое ускорение, какое она сообщила бы ему в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил. Поэтому при расчёте ускорения движения тела все действующие на него силы заменяют одной силой.
Равнодействующей силой называют силу, которая оказывает на тело такое же действие, как и все действующие на него силы вместе.
Равнодействующую силу находят по правилу сложения векторов, она равна геометрической сумме действующих на тело сил.
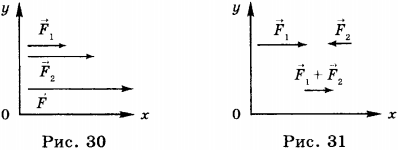
Если силы, действующие на тело, направлены по одной прямой в одну сторону, то \( \vec
Если силы, действующие на тело, направлены в разные стороны, то \( \vec
Если силы направлены под углом друг к другу, то равнодействующая равна диагонали параллелограмма, построенного на действующих на тело силах как на сторонах, или стороне треугольника, начало которой совпадает с началом вектора \( \vec
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Ускорение движения парашютиста с раскрытым парашютом определяется его взаимодействием
1) только с Землёй
2) только с Землёй и с воздухом
3) только с Землёй и с парашютом
4) с Землёй, воздухом и парашютом
2. Сила — это мера
1) быстроты движения
2) инертности
3) взаимодействия
4) быстроты изменения скорости
3. Какие из приведённых ниже величин всегда совпадают по направлению?
1) сила и скорость
2) сила и перемещение
3) сила и ускорение
4) ускорение и перемещение
4. На рисунке а) показаны направления силы, действующей на тело, и его скорости. Какой из четырёх векторов, приведённых на рисунке б), указывает направление ускорения, с которым движется это тело?
5. На тело, находящееся на полу движущегося лифта, действуют сила тяжести 90 Н и сила упругости со стороны пола лифта, равная 75 Н. Чему равна равнодействующая этих сил и как она направлена?
1) 45 Н, направлена в ту же сторону, что и сила тяжести
2) 45 Н, направлена в ту же сторону, что и сила упругости
3) 125 Н, направлена в ту же сторону, что и сила тяжести
4) 125 Н, направлена в ту же сторону, что и сила упругости
6. На тело действуют две силы модули которых, — \( F_1 \) = 30 Н и \( F_2 \) = 40 Н, направленные под углом 90° друг к другу. Чему равна равнодействующая этих сил?
1) 70 Н
2) 50 Н
3) 40 Н
4) 10 Н
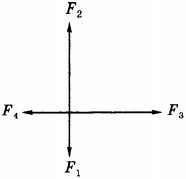
7. Чему равна равнодействующая сил, действующих на тело (рис.), если \( \vec
1) 48 Н
2) 34 Н
3) 28 Н
4) 20 Н
8. Чему равна сила, под действием которой тело массой 8 кг получает ускорение 4 м/с 2 ?
1) 32 Н
2) 8 Н
3) 2 Н
4) 0,5 Н
9. Результат действия силы зависит от
А. Её направления
Б. Точки приложения
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
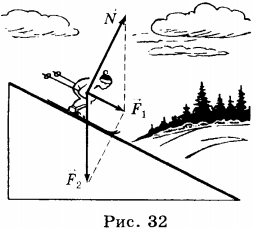
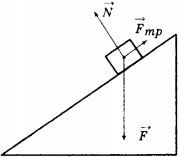
10. На наклонной плоскости покоится брусок, на который действуют сила тяжести \( \vec
11. Установите соответствие между физическими величинами в левом столбце и их единицами в правом столбце. В таблице под номером физической величины левого
столбца запишите соответствующий номер выбранной вами единицы величины из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) масса
Б)сила
B)ускорение
ЕДИНИЦА ВЕЛИЧИНЫ
1) Ньютон (Н)
2) метр в секунду в квадрате (м/с 2 )
3) килограмм (кг)
12. Из приведённых высказываний выберите два верных и запишите их номера.
1) Из двух тел разной массы при действии на них одинаковой силы большее ускорение приобретет тело большей массы.
2) Сила равна произведению массы тела и его ускорения.
3) Направление движения тела всегда совпадает с направлением силы.
4) Сила — причина ускорения тела.
Часть 2
13. На автомобиль массой 1 т действуют сила тяги 1700 Н и сила трения 200 Н. С каким ускорением движется автомобиль?
Источник
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Источник
Способы задания и сложения сил
Сходящаяся система сил.
Геометрический и аналитический методы при определении реакции связи, сходящейся системы сил
Существует два способа задания исложения сил:
В первом случае сила задается ка вектор, во втором с помощью проекций на оси координат.
Рассмотрим, как складываются силы на примере сходящейся системы сил.
Сходящимися называются силы, линии действия которых пересекаются в одной точке. Эти силы могут быть в плоскости и в пространстве.
Геометрический способ
В соответствие с четвертой аксиомой, равнодействующая двух пересекающихся сил приложена к точке их пересечения и определяется как диагональ.
 |
 |
h gyajO0eo4Ioe1uXtTaFz4yb6wHEfasEl5HOtoAmhz6X0VYNW+4Xrkdg7ucHqwHKopRn0xOW2k0kU PUqrW+IPje5x22B13l+sgrdJT5s0fhl359P2+n1YvX/tYlTq/m7ePIMIOIe/MPziMzqUzHR0FzJe dKzTjJMKsgQE28skXYI48rHKMpBlIf8PKH8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA 4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEA OP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA +HWJbMEIAACERAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAA ACEABcn3w98AAAAIAQAADwAAAAAAAAAAAAAAAAAbCwAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAE AAQA8wAAACcMAAAAAA== «>
 |
 |
 |
 |
| β |
| α |
| α |
 1 1 |
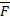 2 2 |
| α |
Равнодействующая будет также действовать как F1и F2. На этих силах можно построить силовой треугольник.
С помощью теоремы синусов можно найти зависимостьсил.
Если имеем систему сходящихся сил, то главный вектор можно определить путём последовательного сложения сил по правилу параллелограмма, но удобнее строить силовой многоугольник.
Система сходящихся сил имеет равнодействующую равную главному вектору этих сил и приложена в точке пересечения.
Из рассуждений очевидно, если силовой многоугольник замкнут, то равнодействующая равна нулю и все силы взаимно уравновешены. Это положение выражает условие равновесия сходящихся сил в геометрической форме.
Для равновесия системы сходящихся сил, приложенных к твердому телу необходимо и достаточно, чтоб равнодействующая равнялась нулю.
Аналитический способ задания и сложения сил.
Силу можно задать с помощью проекции на ось.Проекция вектора 
| α |
 |
 |
| α |
| a |
| b |
| β |
| γ |
| Fy |
| Fx |
| Y |
| X |
| Z |
Проекция силы F на плоскость Оху – вектор Fxy, заключенный между проекциями начала и конца силы F на эту плоскость, т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху Тогда модуль проекции F на плоскость Охубудет равен:  Например, чтобы определить проекцию силы F на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы Fxy на составляющие по осям координат Fx и Fy. Например, чтобы определить проекцию силы F на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы Fxy на составляющие по осям координат Fx и Fy. |
Для сложения сил аналитический служит теорема «о проекции вектора суммы»:
Проекция вектора суммы на ось равна алгебраической сумме слагаемых сил на ту же ось.
  |
 |
 |
 |
 |
 |
 |
 |
  |
   (1) (1) |
 |
Если рассматривается система сходящихся сил в равновесии, то вектор 
Для равновесия любой сходящейся системы сил (на плоскости или в пространстве) необходимо и достаточно, чтоб сумма проекций сил на каждую координатную ось равнялась нулю.
Если силы находятся в одной плоскости, то достаточно двух уравнений.
  |
L AwQUAAYACAAAACEAFJL5fMQAAADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPS2vCQBC+C/0PyxR6 M5s0VNo0q4jU0oMU1ELpbciOSTA7G7JrHv/eFQre5uN7Tr4aTSN66lxtWUESxSCIC6trLhX8HLfz VxDOI2tsLJOCiRyslg+zHDNtB95Tf/ClCCHsMlRQed9mUrqiIoMusi1x4E62M+gD7EqpOxxCuGnk cxwvpMGaQ0OFLW0qKs6Hi1HwOeCwTpOPfnc+baa/48v37y4hpZ4ex/U7CE+jv4v/3V86zE/f4PZM uEAurwAAAP//AwBQSwECLQAUAAYACAAAACEAovhPUwQBAADsAQAAEwAAAAAAAAAAAAAAAAAAAAAA W0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQBsBtX+2AAAAJkBAAALAAAAAAAAAAAA AAAAADUBAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAVAAAAAAAAAAAA AAAAADYCAABkcnMvZ3JvdXBzaGFwZXhtbC54bWxQSwECLQAUAAYACAAAACEAFJL5fMQAAADcAAAA DwAAAAAAAAAAAAAAAACqAgAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA+gAAAJsDAAAAAA== «>
  |
  |
  |
  |
 |
  |
β  |
  |
  |
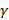  |
Составляем уравнение сходящейся пространственной системы сил.
Силы уравновешиваются. Для определения Т1, Т2, Rcиспользуем аналитические условия равновесия.
Теорема о трех силах
Если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линия этих сил пересекается в одной точке, а силовой треугольник должен быть замкнут.
 |
 |
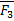 |
 |
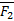 |
Так как тело находится в равновесии под действием трех сил, то 

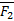 |
 |
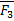 |
При равновесии тела под действием трех сходящихся сил, из линии действия должны пересечься в одной точке.
 |
| β |
 |
Силовой треугольник замкнут.
| X |
 |
| Y |
 |
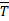 |
Пример 1
Действуют три силы: Т, N, Р
 |
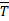 |
 |
 |
 |
 |
| О |
| α |
| Y |
| X |
Геометрический способ
Пример 2
| Так как тело находится в равновесии трех сил, P, T, Ra, то линии действия этих сил должны пересечься в одной точке. |
Решим задачу геометрическим способом
 |
 |
 |
Аналитический метод решения
Составим уравнения равновесия в аналитической форме.
При решении задач данного типа применяется принцип освобождаемости от связи, то есть вместо связей указываются их реакции и нагрузки.
Если число неизвестных величин больше числа уравнений равновесия, то задача статически неопределима, а система сил называется статически неопределимой.
Момент силы.
Момент силы относительно центра и осей
Моментом силы относительно произвольного центра в плоскости действия силы, называется произведение модуля силы на плечо.
Плечо — кратчайшее расстояние от центра О до линии действия силы, но не до точки приложения силы, т.к. сила-скользящий вектор.
G AAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAzIlWHygIAACMMQAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54 bWxQSwECLQAUAAYACAAAACEA14V1ItwAAAAHAQAADwAAAAAAAAAAAAAAAACCCgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA8wAAAIsLAAAAAA== «>
| h |
| M0 |
 |
 |
Знак момента:
По часовой-минус, против часовой-плюс;
Момент силы можно выразить как вектор. Это перпендикуляр к плоскости по правилу Буравчика.
Если в плоскости расположены несколько сил или система сил, то алгебраическая сумма их моментов даст нам главный момент системы сил.
 |
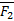 |
 |
 |
 |
 |
 |
Рассмотрим момент силы относительно оси, вычислим момент силы относительно оси Z;
U ACIYzM62xXwCQKxzcMcCxE3p+KDHsMEYBFBbO5htnsvgarNl25P/AwAA//8DAFBLAwQUAAYACAAA ACEAvcVtuN4AAAAHAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBSE74L/YXkFb3Y3apqS5qWU op6KYCuIt9fkNQnN7obsNkn/vevJHocZZr7J1pNuxcC9a6xBiOYKBJvClo2pEL4Ob49LEM6TKam1 hhGu7GCd399llJZ2NJ887H0lQolxKSHU3neplK6oWZOb245N8E621+SD7CtZ9jSGct3KJ6UWUlNj wkJNHW9rLs77i0Z4H2ncPEevw+582l5/DvHH9y5ixIfZtFmB8Dz5/zD84Qd0yAPT0V5M6USLkCSL kER4ARHcRKlw5IgQx0sFMs/kLX/+CwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAAT AAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/W AAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAE8ZM7lo CQAA+k0AAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAL3F bbjeAAAABwEAAA8AAAAAAAAAAAAAAAAAwgsAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMA AADNDAAAAAA= «>
| b |
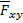 |
| a |
| h |
| Y |
| X |
| Z |
| A |
L AwQUAAYACAAAACEAJqo52MIAAADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPTYvCMBC9C/sfwizs TdO6Kks1ioiKBxGswuJtaMa22ExKE9v6781hYY+P971Y9aYSLTWutKwgHkUgiDOrS84VXC+74Q8I 55E1VpZJwYscrJYfgwUm2nZ8pjb1uQgh7BJUUHhfJ1K6rCCDbmRr4sDdbWPQB9jkUjfYhXBTyXEU zaTBkkNDgTVtCsoe6dMo2HfYrb/jbXt83Dev22V6+j3GpNTXZ7+eg/DU+3/xn/ugFUyiMD+cCUdA Lt8AAAD//wMAUEsBAi0AFAAGAAgAAAAhAKL4T1MEAQAA7AEAABMAAAAAAAAAAAAAAAAAAAAAAFtD b250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAbAbV/tgAAACZAQAACwAAAAAAAAAAAAAA AAA1AQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAFQAAAAAAAAAAAAAA AAA2AgAAZHJzL2dyb3Vwc2hhcGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhACaqOdjCAAAA3AAAAA8A AAAAAAAAAAAAAAAAqgIAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPoAAACZAwAAAAA= «>
| B |
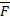 |
| α |
Спроецируем Fна XY;
Момент силы относительно оси равен моменту ее проекции на плоскость перпендикулярную оси, взятому на пересечении осей и плоскости
Если сила параллельна оси или пересекает ее, то mz(F)=0
Дата добавления: 2018-02-28 ; просмотров: 1119 ; Мы поможем в написании вашей работы!
Источник