Сетевые модели графический способ

Графический метод расчета параметров сетевого графика

Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.

Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.

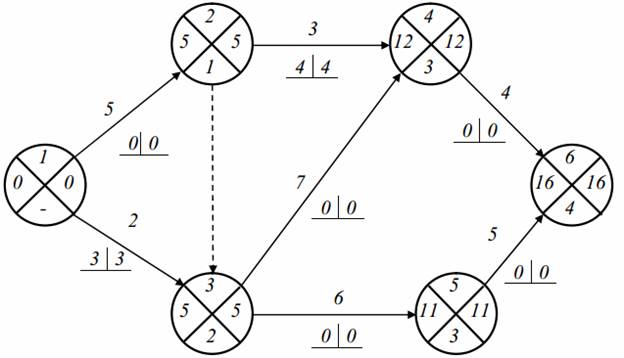
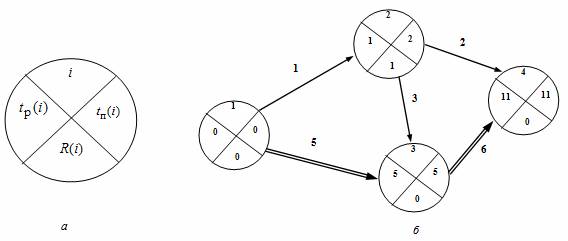
Пример . Определим параметры для событий и критический путь на графике. На практике получил широкое распространение четырехсекторный способ расчета ранних и поздних сроков свершения событий. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис. 2, а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события t_p(i), в правом – наиболее позднее из допустимых время свершения события t_п(i), в нижнем – резерв времени данного события R(i).

Раннее время свершения события t_p(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: t_p(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим t_p(i). Всегда для начального события t_p(1)=0.
Для события 3 (рис., б) – t_p(3)=max<1+3,0+5>=5; для события 4 – t_p(4)=max<1+2,5+6>=11.
Длина критического пути L_кр=11. Послойно, переходя от конечного события до начального, определим t_п(i). Всегда для конечного события t_п(4)=t(L_кр)=11. Позднее время свершения события t_п(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(L_кр), можно найти t_п(i)= t(L_кр)-max(t) после (i).
Для события 2 – t_п(3)=11-max<3+6,2>=2.
Для критического пути время раннего свершения события t_p(i) равно времени позднего свершения этого события t_п(i), т.е. t_p(i)= t_п(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= t_п(i)- t_p(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.

Источник

Сетевые модели графический способ

«Организация, планирование и управление строительным производством» под общей редакцией профессора И.Г.Галкина, Москва, «Высшая школа», 1978г. стр. 89-121

Сетевая модель календарного плана

Недостатки линейных календарных планов в значительной мере устраняются при использовании сетевых моделей, позволяющих не только рассчитать основные параметры графика, определяющие продолжительность выполнения программы в целом и сроки начала и окончания взаимосвязанных работ в составе комплекса, но и анализировать график, выявлять резервы и использовать их для его улучшения (оптимизации).

Сетевая модель календарного плана является наиболее удачной для отражения вероятностных производственных процессов. Она позволяет в более наглядной форме отобразить порядок возведения сложного объекта.

В строительной практике построение сетевого графика преимущественно ведется по типу «работы-дуги», поскольку при большом числе входящих и выходящих работ для одного события такой тип построения графика оказывается наиболее удобным.

При таком построении работа в сетевом графике изображается сплошной стрелкой, причем в зависимости от характера графика и степени его детализации одной стрелкой может быть изображен комплекс работ, либо отдельная операция. На рис. 1 сплошными стрелками (дугами) показаны работы — предшествующая, данная работа и последующая. Стрелки в сетевом графике не имеют масштаба и определенного угла наклона, однако все они должны иметь направление, ведущее от начала к завершению программы, т. е. слева направо.

У начала программы стоит исходное событие, не имеющее непосредственно предшествующих событий. Событие у начала любой работы называют начальным или предшествующим, а у конца работы — конечным или последующим.

К каждому событию может непосредственно примыкать несколько предшествующих (входящих) работ и несколько последующих (выходящих) работ, Событие в этом случае отражает совокупность условий, позволяющих начать одну или несколько работ лишь при окончании некоторых других (непосредственно предшествующих) работ.

В конце программы стоит завершающее событие, не имеющее непосредственно следующих работ.
Для точного обозначения предшествования одной работы другим работам в необходимых случаях вводятся дополнительные дуги (в виде пунктирных стрелочек), выполняющие функции связей (или фиктивных работ) (рис. 2 ).

Для удобства кодирования и анализа сети не допускают, чтобы несколько параллельно выполняемых работ имели общие начальные или общие конечные события. На рис. 3 показан фрагмент такого графика с вводом дополнительных связей. Между исходным и завершающим событием лежит несколько технологически связанных между собой цепочек работ, выполняемых последовательно. Поскольку к некоторым событиям примыкают «входящие» и «выходящие» работы, выполняемые параллельно, цепочки последовательно выполняемых работ как бы пересекаются, образуя сеть с узлами в местах событий.

Как указывалось выше, событие фиксирует состояние, а не является процессом, требующим затрат времени или труда. Все события нумеруются от исходного до завершающего.

Сетевые модели могут быть одноцелевые и многоцелевые.

Одноцелевой сетевой моделью называют сетевой график, который составлен для достижения единственной цели. Завершающее событие в такой графике является целевым событием.

Многоцелевые сети предусматривают достижение нескольких целей, в том числе промежуточных.

Для оперативного контроля к управления строительством при планировании в сетевом графике могут быть выделены контрольные события, привязанные к календарным датам. Каждая работа характеризуется продолжительностью ее выполнения, получаемой в результате подсчета объема работ, трудоемкости, выбора метода ее выполнения, средств механизации и состава рабочей бригады.

В комплексе работ, отраженном на сетевом графике, имеются работы, выполняемые последовательно и параллельно. При рассмотрении какой-либо работы в сети различают непосредственно предшествующую ей работу и последующую.

При наличии данных о продолжительности выполнения каждой работы в сетевом графике представляется возможным проследить все цепочки последовательно выполняемых работ от исходного события до завершающего и определить общую продолжительность каждой цепочки. Самый продолжительный по времени путь от исходного до завершающего события называют критическим. Им определяется продолжительность выполнения всей программы работ.

Критический путь обозначается на графике двойными или жирными стрелками. Близкие к критическому по продолжительности пути называют подкритическими. Все другие, менее продолжительные пути называют некритическими и работы, лежащие на этих путях,— некритическими. Не исключено, что в одном графике может быть два и даже несколько критических (равных по продолжительности) путей.

В зависимости от размера сетевого графика (числа работ и событий) количество критических работ, т. е. лежащих на критическом пути, обычно бывает не более 10-15% от общего числа работ, что позволяет руководителям строительства сосредоточивать внимание прежде всего на этих работах, от которых зависит соблюдение установленного общего срока строительства.

Сетевые модели бывают детерминированные и вероятностные. В последних учитываются некоторые неопределенные данные о параметрах, составе и порядке выполнения работ.

Простейшая одноцелевая модель с учетом времени (ПДВ—простейшая детерминированная временная) должна в качестве исходной информации иметь единственное исходное событие i0 и единственное завершающее событие.

Продолжительность каждой работы в сети, т. е. временная1 опенка дуги (стрелки) обозначается t_i-j.

В качестве исходной информации задается начало выполнения комплекса работ, а в некоторых случаях — директивная продолжительность строительства или срок ввода в действие объекта.

На основе расчета модели определяется критическое время T_кр, т. е. минимальное время, в течение которого может быть осуществлена программа. Остальные параметры сетевого графика имеют следующие обозначения:

t_h-i — продолжительность предшествующей работы;
t_i-j — продолжительность данной работы, у которой предшествующее событие i, а последующее j;
t_j-k — продолжительность последующей работы;
t рн _i-j— раннее начало работы;
t ро _i-j — раннее окончание работы;
t пн _i-j — позднее начало работы;
t по _i-j — позднее окончание работы;
R_i-j— полный запас времени работы;
r_i-j—частный запас времени работы.

Источник

Анализ сетевого графика

Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне

Размеры графического полотна

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Инструкция к сервису

Основные определения

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 2 . Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3 . При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка
завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Источник

Графические и сетевые модели

Широкое распространение в экономических расчетах нашли сетевые модели. Наиболее часто они применяются при построении сквозных графиков выпуска продукции с опережением — основного документа оперативно-календарного плана.

Графическая модель позволяет воспроизвести методы согласования частных производственных процессов, найти резервы повышения параллельности производственного цикла, определить наиболее предпочтительные варианты сокращения цикла.

Сетевой график содержит два типа элементов: работы и события. События представляют начало или окончание каждого вида работ, которые четко фиксируются в начальной и конечной стадиях.

Начальным (исходным) событием называется момент начала первых работ, связанных с подготовкой и реализацией запланированного мероприятия, конечное событие завершается достижением поставленной цели.

Таким образом, сетевой график отражает логическую последовательность событий, ведущих к поставленной цели.

На графике события обозначаются кружками с указанными в них номерами, а выполняемая работа — стрелкой, соединяющей последовательно связанные события,

Продолжительность работы обозначается не длиной стрелки, а числом единиц времени, которое указывается над стрелкой (это может быть число дней или месяцев). Под стрелкой указываются затраты на проведение работы (рубли, чел.-дни).

Сетевой график позволяет наиболее рационально построить план работы, установить строгую последовательность и очередность для выполнения всех операций и действий. С помощью сетевого графика можно точно определить сроки свершения каждого события и срок достижения результата.

Сетевой график составляется на каждый тип нового изделия. С помощью сетевого графика можно показать полный путь движения к цели в виде цепочки взаимосвязанных работ и событий, включающей затраты времени и средств на них, а также представить другие возможные варианты действий.

Таким образом, сетевой график позволяет составить наиболее рациональный план осуществления мероприятий, установить строгую очередность операций, их сроки, организовать контроль.

Календарные планы производственных подразделений

Календарные планы производственных подразделений предприятия строятся на срок не более квартала, а иногда на месяц. Построение планов и их взаимосвязь ведется в направлении обратном ходу технологического процесса, от завершающей стадии производства к предшествующим.

На первом шаге формируется календарный план производства готовой продукции на завершающей стадии производства. (Например, календарный план сборочного цеха).

Затем рассчитываются плановые потребности во всех комплектующих на выпуск готовой продукции и крайние сроки их выпуска, исходя из сроков выпуска готовой продукции и деятельности ее производственного цикла. На основе этой информации рассчитываются календарные планы производства для каждого подразделения и обосновываются с точки зрения имеющихся ресурсов на выполнение этих планов в каждом производственном подразделении.

Календарное планирование каждого рабочего места осуществляется в рамках оперативного планирования внутри производственного подразделения. Основная задача и проблема на этом этапе — выбор оптимальной (с точки зрения рациональной работы всего подразделения) очередности выполнения различных работ на каждом рабочем месте. Плановое задание каждому рабочему должно быть составлено так, чтобы были соблюдены сроки выпуска продукции, содержащиеся в календарном плане подразделения, с одной стороны, с другой, должно быть обеспечено эффективное использование всех ресурсов подразделения: перерывы между работами на каждом рабочем месте должны быть минимальны, должна быть обеспечены максимальная производительность и требуемое качество.

График изготовления продукта

Для установления последовательности работы цехов и служб производства составляется график изготовления продукта. При составлении графика делается развернутый расчет длительности цикла изготовления продукта цепным методом в порядке, обратном ходу производственного процесса. От срока передачи образца продукта на испытания определяется время цикла общей сборки, агрегатной сборки и т.д. Далее уточняются циклы выполнения отдельных операций, параллельность их выполнения с целью минимизации общего цикла. Работа остальных служб согласуется с планами и потребностями основных цехов на основе опережения сроков начала работ в основных цехах.

График изготовления продукта является основой оперативного планирования по запуску изделий в производство.

В качестве инструмента оперативного управления производством часто используется учетно-плановый график Ганта (или его компьютерные версии), который можно применять на всех этапах оперативного управления производством: при планировании, диспетчеризации, выдаче нарядов на работу, контроле сроков выполнения работ

Рассмотрим пример: в производительном подразделении четыре рабочих места, за неделю должно быть изготовлено шесть изделий. Данные о технологическом маршруте и трудоемкости выполнения каждой работы по изделиям даны в таблице:

РМ — рабочее место

Результаты распределения работ по дням недели и рабочим местам выглядят так, как показано ниже:

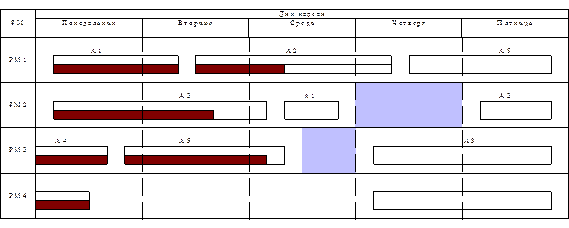
— планируемое время работы

— планируемая остановка рабочего места на ремонт или профилактику

— фактический ход производственного процесса, выполненные объемы работ

С помощью графиков Гантта можно осуществить учет и контроль производства. Как видно из схемы, обработка изделия А 2 на РМ 1 идет с опережением, обработка изделия А 5 тоже. В то же время обработка изделия А 3 на РМ 2 опаздывает. РМ 4 простаивает, так как обработку изделия А 1 нельзя начать, пока не будет закончена обработка этого изделия на РМ 2. На основе этого анализа менеджер должен осуществить соответствующие корректирующие воздействия.

Дата добавления: 2016-11-02 ; просмотров: 732 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник