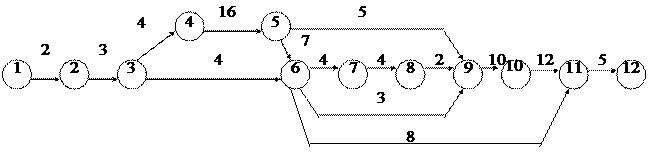Сетевой график это графический способ изображения

Анализ сетевого графика

Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне

Размеры графического полотна

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Инструкция к сервису

Основные определения

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 2 . Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3 . При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка
завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Источник

Сетевые графики и правила их построения

Сетевой график – это графическое изображение процессов, выполнение которых необходимо для достижения поставленной цели.

Методы сетевого планирования и управления (СПУ) базируются на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. В экономике обычно используются два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины. Сеть — это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, каждый сетевой график представляет собой сеть, состоящую из узлов(вершин) и соединяющих их ориентированных дуг (ребер). Узлы графика называются событиями, а соединяющие их ориентированные дуги — работами. На сетевом графике события изображаются кружками или иными геометрическими фигурами, а соединяющие их работы безразмерными стрелками (безразмерными они называются потому, что длина стрелки не зависит от объема работы, которую она отражает).

Каждому событию сетевого графика приписывают определенный номер (i), а работу, соединяющие события, обозначают индексом (ij). Каждая работа характеризуется своей продолжительностью (длительностью) t(ij). Значение t(ij) в часах или днях проставляют в виде числа над соответствующей стрелкой сетевого графика.

В практике сетевого планирования используют несколько типов работ:

1) реальная работа, производственный процесс, который требует затрат труда, времени, материалов;

2) пассивная работа (ожидание), естественный процесс, который не требует затрат труда и материальных ресурсов, но осуществление которого может происходить лишь в течение определенного периода времени;

3) фиктивная работа (зависимость), которая не требует никаких затрат, но показывает, что какое-то событие не может свершиться ранее другого. При построении графика такие работы обычно обозначают пунктирной линией.

Каждая работа самостоятельно или в сочетании с другими работами заканчивается событиями, которые выражают результаты выполненных работ. В сетевых графиках выделяют следующие события: 1) исходное, 2) промежуточные, 3) завершающее (окончательное). Если событие имеет промежуточный характер, то оно является предпосылкой для начала следующих за ним работ. Считается, что событие не имеет продолжительности и осуществляется мгновенно после выполнения предшествующих ему работ. Исходному событию не предшествуют никакие работы. Оно выражает собой момент наступления условий для начала выполнения всего комплекса работ. Завершающее событие не имеет никаких последующих работ и выражает собой момент окончания всего комплекса работ и достижения намеченной цели.

Взаимосвязанные работы и события сетевого графика образуют пути, которые соединяют исходные и завершающие события, их называют полными. Полный путь на сетевом графике представляет собой последовательность работ по направлению стрелок от исходного до завершающего события. Полный путь максимальной продолжительности называется критическим. Продолжительность критического пути определяет конечный срок выполнения всего комплекса работ и достижения намеченной цели.

Работы, расположенные на критическом пути, называют критическими или напряженными. Все остальные работы считаются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения и сроки свершения событий, не влияя на общую продолжительность выполнения всего комплекса работ.

Правилапостроения сетевого графика.

1. Сеть вычерчивается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.

2. Два соседних события могут соединяться лишь одной работой. При изображении параллельных работ не допускается, чтобы они имели общие начальные и конечные события, так как в этом случае они будут иметь одинаковую нумерацию. Для изображения параллельных работ вводится промежуточное событие и фиктивная работа.

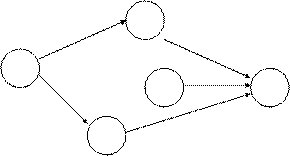
3. В сети не должно быть «тупиков», то есть все события, кроме завершающего, должны иметь последующую работу (тупиками называются промежуточные события, из которых не выходит ни одна работа). Такая ситуация может иметь место, когда данная работа не нужна или какая-либо работа пропущена.

4. В сети не должно быть событий, кроме исходного, которым не предшествует хотя бы одна работа. Такие события называются «хвостовыми». Это может иметь место в случае пропуска предшествующей работы.

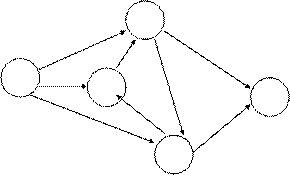
5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь

Для правильной нумерации событий сетевого графика используют следующую схему действий. Нумерацию начинают из исходного события, которому присваивают номер 0 или 1. Из начального события (1) вычеркивают все исходящие из него работы (ориентированные дуги), и на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию присваивают номер (2). Указанная последовательность действий повторяется до тех пор, пока не буду пронумерованы все события сетевого графика. Если при очередном вычеркивании одновременно возникают два события, не имеющие входящих работ, то номера им присваиваются произвольно. Номер завершающего события должен быть равен количеству событий в сетевом графике.

В процессе построения сетевого графика важное значение имеет определение продолжительности выполнения каждой работы, то есть необходимо дать ей временную оценку. Продолжительность выполнения работ устанавливают либо в соответствии с действующими нормативами, либо на основе экспертных оценок. В первом случае оценки продолжительности называют детерминированными, во втором — стохастическими.

Существуют различные варианты расчета стохастических временных оценок. Рассмотрим некоторые из них. В первом случае устанавливают три вида продолжительности выполнения конкретной работы:

1) максимальный срок, который исходит из наиболее неблагоприятных условий выполнения работы (t_max);

2) минимальный срок, который исходит из наиболее благоприятных условий выполнения работы (t_min);

3) наиболее вероятный срок, исходящий из реальной обеспеченности работы ресурсами и наличия нормальных условий ее выполнения (t_в).

На основе этих оценок рассчитывается ожидаемое время выполнения работы (ее временная оценка) по формуле

. (5.1)

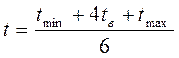
Во втором случае задаются две оценки — минимальная (t_min) и максимальная (t_max). Продолжительность работы в этом случае рассматривается как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Ожидаемое значение данных оценок (t_ож) (при бета-распределении плотности вероятности) оценивается по формуле

. (5.2)

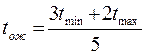
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии (S 2 )

. (5.3)

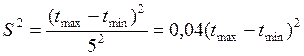
Построение любого сетевого графика начинается с составления полного перечня работ. Затем устанавливается очередность работ, и для каждой конкретной работы определяются непосредственно предшествующие и последующие работы. Для установления границ каждого вида работ используются вопросы: 1) что должно предшествовать данной работе и 2) что должно следовать за данной работой. После составления полного перечня работ, установления их очередности и временных оценок, приступают непосредственно к разработке и составлению сетевого графика.

Рассмотрим в качестве примера программу строительства здания склада. Перечень операций, их последовательность и временную продолжительность оформим таблицей.

Перечень работ сетевого графика

Операция	Описание операции	Непосредственно предшествующая операция	Продолжитель-ность, дн.
А	Расчистка строительной площадки	—
Б	Выемка котлована под фундамент	А
В	Уклада фундаментных блоков	Б
Г	Прокладка наружных инженерных сетей	Б
Д	Сооружение каркаса здания	В
Е	Кровельные работы	Д
Ж	Внутренние сантехнические работы	Г, Е
З	Настилка полов	Ж
И	Установка дверных и оконных рам	Д
К	Теплоизоляция перекрытий	Е
Л	Прокладка электропроводной сети	З
М	Штукатурка стен и потолков	И, К, Л
Н	Внутренняя отделка	М
О	Наружная отделка	Е
П	Благоустройство территории	Н, О

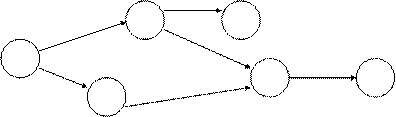
Построенный на основании данных табл. 5.1 предварительный сетевой график выполнения работ выглядит следующим образом (рис. 5.1).

Рис. 5.1. Предварительный сетевой график

Ниже приведен тот же самый график строительства складского здания, пронумерованный и с проставленными временными оценками работ (рис. 5.2).

Рис. 5.2. Окончательный вариант сетевого графика

Источник

Построение сетевого графика

Каждый менеджер проекта сталкивается с такой типовой для него задачей, как построение сетевого графика. В настоящее время этот процесс полностью автоматизирован и, как правило, у менеджера не возникает больших проблем. Уже давно нет необходимости чертить на бумаге графики, высчитывать ранние и поздние начала или окончания задач, соединять задачи стрелками, вычислять длину критического пути. ИСУП успешно решает все эти задачи.

Однако, без понимания основ и правил построения сетевых графиков менеджеры проектов довольно-таки часто совершают ошибки. Несмотря на то, что современные ИСУП достаточно «умные» и подстраховывают менеджера проекта во многих моментах, связанных с расписанием проекта, тем не менее, остаются «слепые» зоны, которые лежат только в зоне ответственности менеджера проекта.

Для того, чтобы получить настоящую пользу от ИСУП, ей надо уметь грамотно пользоваться, как и любым другим инструментом.

Что такое сетевой график

Сетевой график (англ., Project Network) — это динамическая модель проекта, отражающая зависимость и последовательность выполнения работ проекта, связывающая их завершение во времени с учётом затрат ресурсов и стоимости работ.

Сетевой график может быть построен в двумя способами:

• Вершины графа отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте.
• Вершины графа отражают работы, а связи между ними — зависимости между работами.

Правила построения сетевого граифка

Прежде всего, построение сетевого графика заключается в правильном соединении между собой событий (на схеме обозначаются кружками) с помощью работ (на схеме обозначаются стрелками). Правильность соединения стрелок заключается в следующем:

• каждая работа в сетевом графике должна выходить из события, которое означает окончание всех работ, результат которых необходим для начала работы;
• событие, обозначающее начало определенной работы не должно включать в себя результаты работ, завершение которых не требуется для начала этой работы;
• сетевой график строится слева направо, и каждое событие с большим порядковым номером должно быть расположено правее предыдущего. Стрелки, изображающие работы, должны также располагаться слева направо.

Исходные работы

Построение графика начинается с изображения работ, не требующих для своего начала результатов выполнения других работ. Такие работы можно назвать исходными, так как все остальные работы комплекса будут выполняться только после их полного выполнения.

В зависимости от специфики планируемого комплекса, исходных работ может быть несколько, а может быть только одна. Размещая исходные работы необходимо учитывать, что на сетевом графике, должно быть только одно исходное событие.

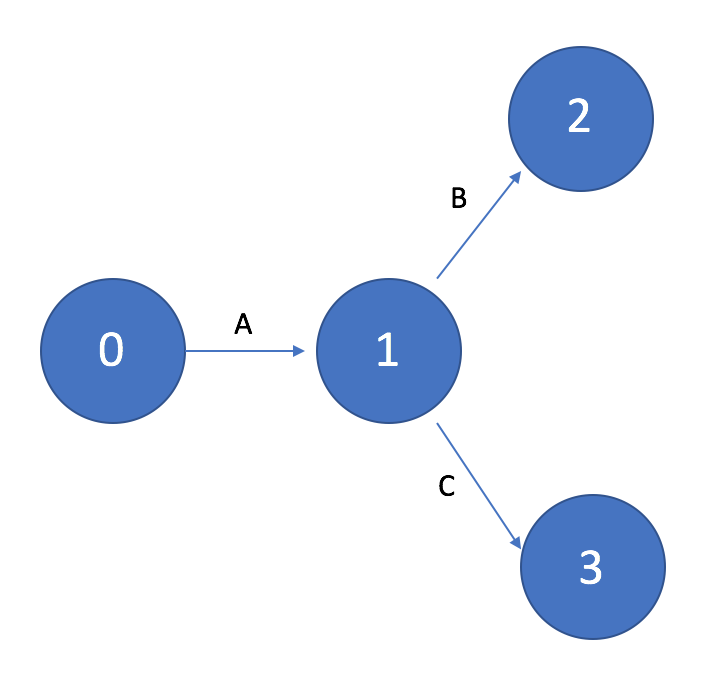
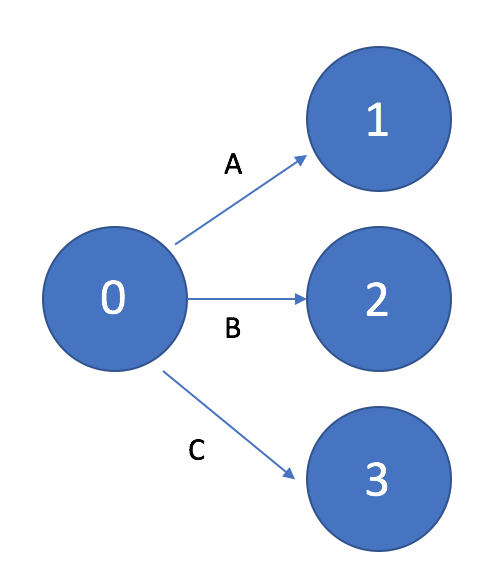
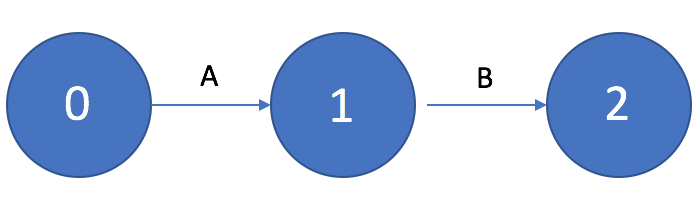
На рисунке 1 показан пример начала сетевого графика с одной исходной работой (работа A), а на рисунке 2 пример начала сетевого графика с тремя исходными работами (работы A, B, C).

Рисунок 1. Сетевой график с одной исходной работой

Рисунок 2. Сетевой график с тремя исходными работами

Последовательные работы

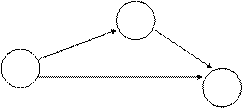
Если работа B должна выполняться только после выполнения работы A, то на графике это изображается в виде последовательной цепочки работ и событий.

Рисунок 3. Последовательно выполняемые работы

Работы, выполняемые после одной и той же работы

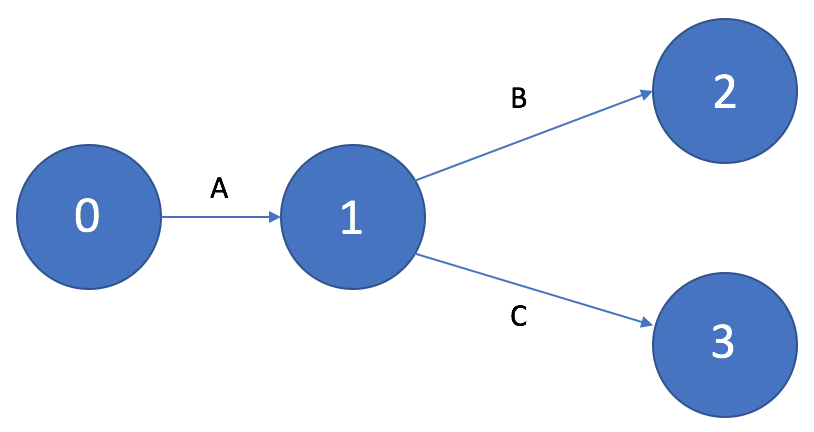
Если для выполнения нескольких работ, например, B и C необходим результат одной и той же работы A, то на графике это изображается «параллельными» стрелками, выходящими из события, являющегося результатом выполнения работы А.

Рисунок 4. Работы, выполняемые после одной и той же работы

Работа, выполняемая после нескольких работ

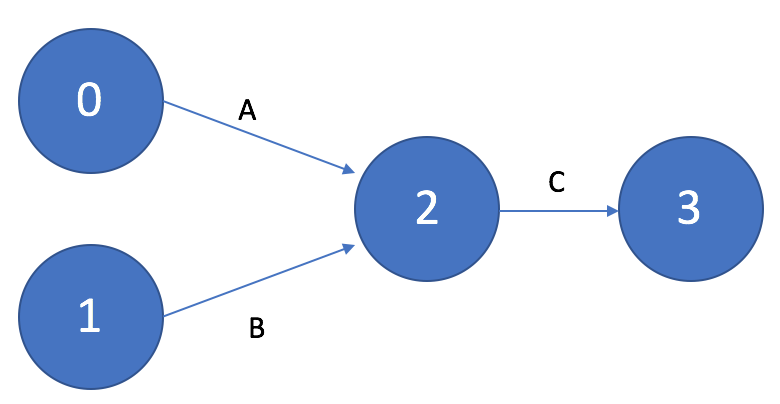
Если для выполнения работы C необходим результат работ A и B, то на графике это изображается «параллельными» стрелками, входящими в событие, после достижения которого следует работа C.

Рисунок 5. Работа, выполняемая после нескольких работ

Работы, выполняемые после частичного выполнения других работ

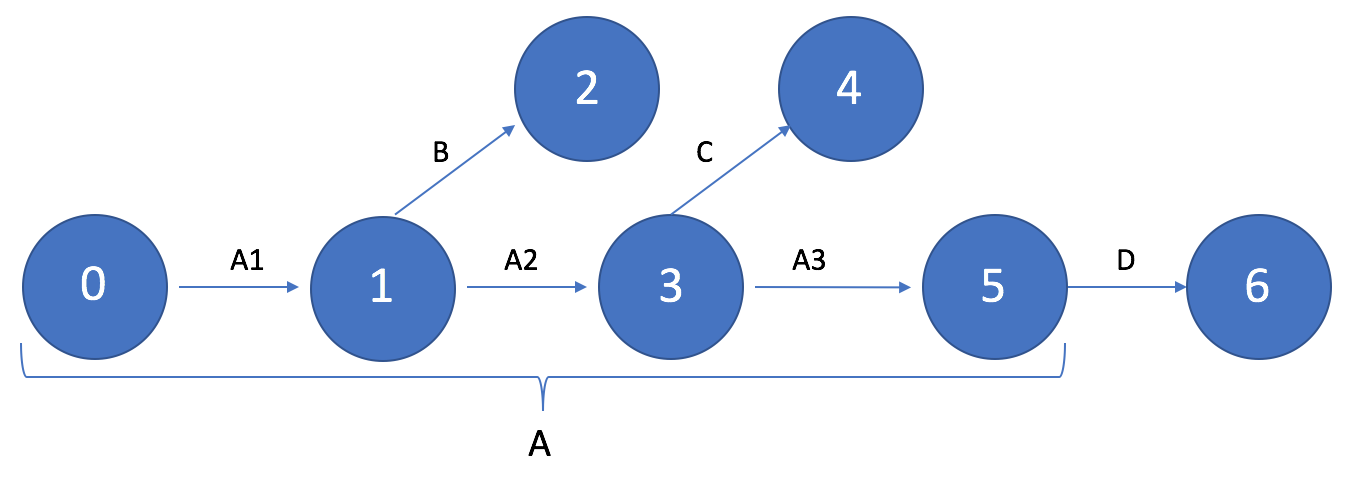
Если для выполнения работ B и C необходим промежуточный результат работы A, то работа A разбивается на подзадачи таким образом, чтобы первая ее подзадача (A1) выполнялась до получения промежуточного результата, необходимого для начала работы B, а вторая подзадача выполнялась до получения промежуточного результата, необходимого для начала работы C, последующая же часть A3, может выполняться параллельно с работами A1 и A2.

Рисунок 6. Работы, выполняемые после частичного выполнения других работ

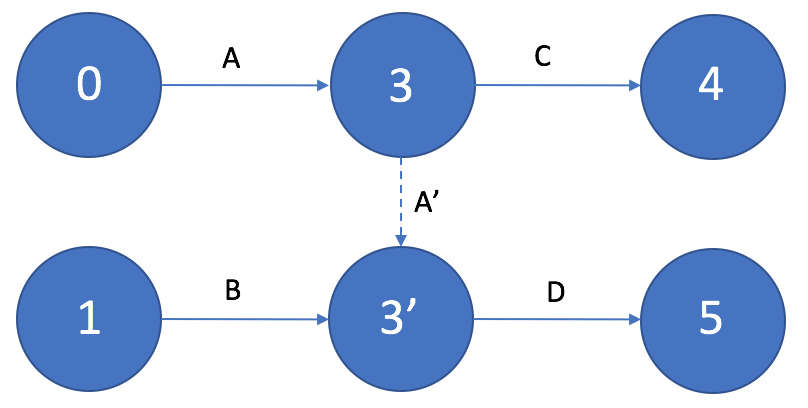
Работы, имеющие общие начальное и конечное события

Два соседних события могут быть объединены одной и только одной работой. Для изображения параллельных работ на сетевом графике вводится так называемое промежуточное событие и фиктивная работа.

Рисунок 7. Работы, имеющие общие начальное и конечное события

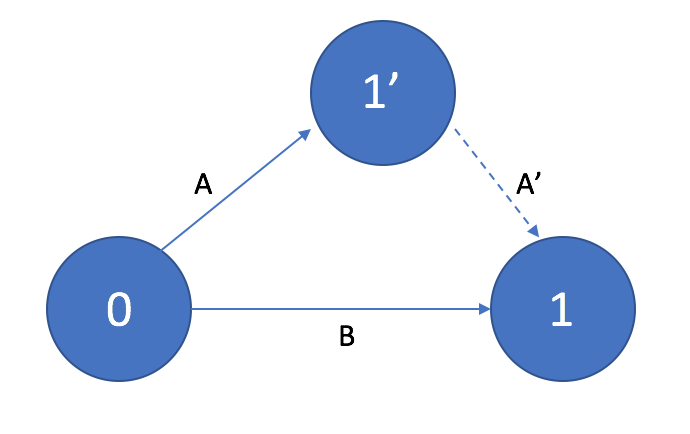
Использование фиктивных работ

Если выполнение работы D возможно только после получения совокупного результата работ A и B, а выполнение работы C – после получения только результата работы А, то в сетевом графике необходимо ввести дополнительное событие и фиктивную работу.

Рисунок 8. Использование фиктивных работ

«Хвосты» и «тупики»

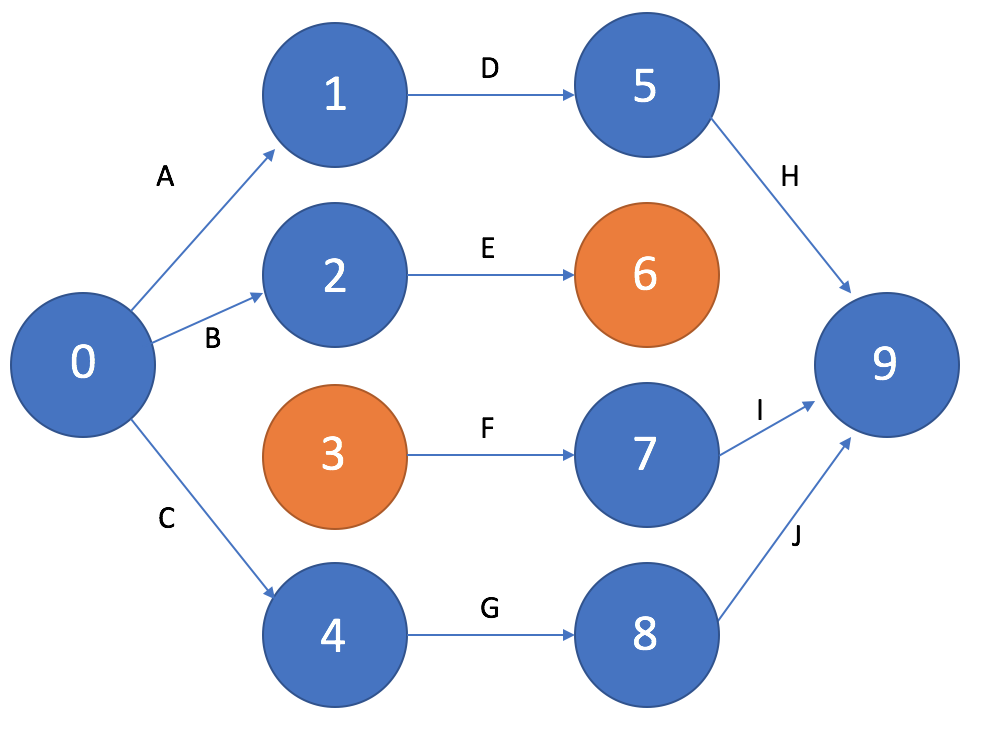
В сети не должно быть «тупиков», т.е. промежуточных событий, из которых не выходит ни одна работа. На рисунке 9 тупиковым событием является событие 6.

Также не должно быть «хвостов», т.е. промежуточных событий, которым не предшествует хотя бы одна работа. На рисунке 9 хвостовым событием является событие 3.

Рисунок 9. «Хвосты» и «тупики» в сетевом графике

Циклы

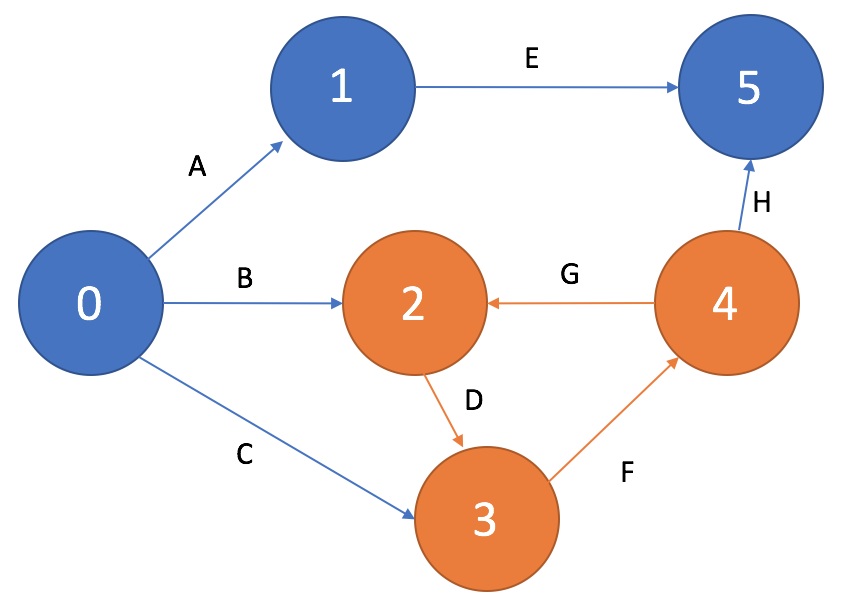
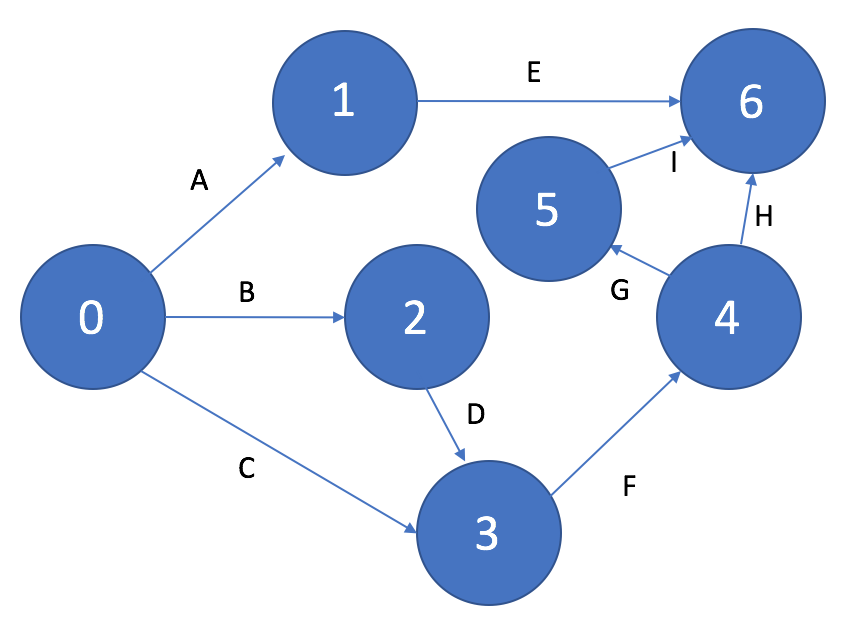
На сетевом графике не должно быть циклов, состоящих из взаимосвязанных работ, создающих замкнутую цепь — цепочка работ D->F->G на рисунке 10. Данная ситуация скорее всего свидетельствует об ошибке при составлении перечня работ и определении их взаимосвязей.

Рисунок 10. Цикл на сетевом графике

В таком случае необходимо проанализировать исходные данные и в зависимости от сделанных по итогам анализа выводов, либо перенаправить работу создающую цикл в другое событие (если работам, начинающимся в этом событии требуется ее результат, или если она является частью общего результата), либо совсем исключить ее из комплекса (если выявлено, что ее результат не требуется).

На рисунке 11 приведен пример устранения цикла, когда работа G становится частью общего результата.

Рисунок 11. Устранение цикла на сетевом графике

Именование работ и нумерация событий

Каждая работа в сетевом графике должна определяться однозначно, только ей присущей парой событий, как и не должно быть на графике событий с одинаковыми номерами.

Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 0. Из исходного события вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 1. Затем вычеркивают работы, выходящие из события 1, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 2, и так продолжается до завершающего события.

Источник