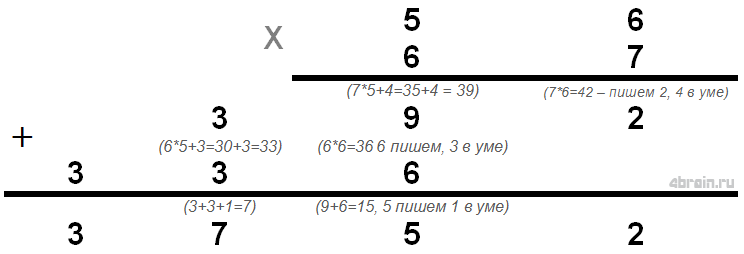Самый простой способ умножения двузначных чисел

Урок 3. Традиционное умножение в уме

Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга.

В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.

Первый способ – раскладка на десятки и единицы

Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:

• Первое действие: 60*80 = 4800 — запоминаем
• Второе действие: 60*5+3*80 = 540 – запоминаем
• Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.

Второй способ – арифметические подгонки

Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:

Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.

Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.

Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.

Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.

Третий способ — мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик.

Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков

Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.

Второе действие: 56*6=300+36=336 (ну или 392-56)

Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.

Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.

Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.

Источник

Искусство умножения двузначных чисел в уме

Люди всегда стремились найти лучшие способы выполнения вычислений. Чем стремительнее развивается прогресс, тем более актуальными становятся высокие математические способности. Даже тот человек, карьера которого не предполагает работу с цифрами, ежедневно вынужден прибегать к счету в уме. Походы за покупками, оплата коммунальных счетов, планирование семейного бюджета – все это требует большого количество подсчетов. Конечно, можно полагаться на технику, ведь в каждом современном смартфоне присутствует калькулятор. Но все же стоит помнить, что умение быстро считать – это возможность существенно оптимизировать свои собственные ресурсы, поэтому развивать такие навыки важно.

Умножение в уме

В современном мире цифры окружают нас везде. Ежедневно мы не задумываясь выполняем десятки и даже сотни простых арифметических действий, но, стоит только столкнуться с более сложными числовыми операциями, и большинство людей машинально потянется к калькулятору. Мало кто хочет тратить время на сложные подсчеты в уме, когда с помощью информационных технологий произвести их можно за считанные секунды. Но что делать, если смартфона, калькулятора или листа бумаги с ручкой нет, а что-то посчитать нужно срочно? На помощь приходят методы счета в уме.

Складывать и вычитать устно – этому человек учится еще в школе. Со временем, удается научиться без труда производить вычисления даже с большими значениями. Конечно, это утверждение справедливо только для простых операций, таких как сложение и вычитание, а вот умножение освоить уже не так легко. В школе от детей требуется научиться умножать только на множитель от одного до десяти, а более сложные подсчеты допустимо производить на бумаге. Таким образом, ученикам не прививается умение выполнять умножение больших чисел в уме, этим навыкам можно обучиться только дополнительно.

Умение быстро считать очень полезно, так как оно используется ежедневно. Поэтому сегодня придумано множество подходов к счету. Чаще всего люди используют различные математические приемы, которые позволяют производить умножение устно. Они имеют свои плюсы и минусы, но все же позволяют получить правильный ответ без использования подручных средств. Чтобы определить, насколько эти способы эффективны и продуктивны в повседневных реалиях, нужно рассмотреть каждый из них отдельно.

Популярные методы устного умножения

Сегодня существует сразу несколько способов умножения в уме. Они не универсальны, но позволяют достаточно успешно производить операции с двузначными числами. Чтобы подобрать для себя оптимальный, лучше ознакомиться с самыми популярными из них:

Вариант 1. Умножение в столбик

Этот вариант отлично подходит тем, кто способен хорошо запоминать и удерживать в памяти сразу несколько промежуточных результатов вычислений. Благодаря этому подходу можно легко производить операции между двузначными числами. Рассмотрим данный вид счета на примере выражения 34*63.

Сначала необходимо умножить 34 на единицы второго числа: 34*3=102. Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142

Вариант 2. Умножение с разложением на десятки и единицы

Этот вариант также требует хорошей памяти. Рассмотрим его на примере прошлого выражения 34*63.

Сначала требуется разложить числа на десятки и единицы, у нас получится: (30+4)*(60+3). Далее мы перемножаем между собой десятки: 30*60=1800. Запоминаем этот результат. Затем необходимо умножить десятки первого значения на единицы второго и наоборот: (30*3)+(60*4)=330. Теперь наступает самая сложная часть, главное – не сбиться. Нам нужно сложить результаты наших первых двух примеров и прибавить к ним произведение единиц перемножаемых чисел. Получится следующее выражение: 1800+330+4*3=2142.

Вариант 3. Умножение с большими числами

Этот вид вычислений больше подходит для тех двузначных чисел, которые близки к 100. Рассмотрим этот способ на примере выражения 88*95.

Сначала нужно представить каждое из этих значений как разность 100 и другого числа: 100-a=88 и 100-b=95, a=12, b=5. Так у нас получится (100-12)*(100-5). Теперь нужно произвести следующие вычисления: 88-b и 95-a, 88-5 и 95-12, получится 83 в обоих случаях. Это значение нужно запомнить. Теперь нам нужно найти a*b=12*5=60. Наш итоговый ответ будет состоять из четырех цифр от полученных ранее ответов: 83 и 60, получается 8360.

Иногда в результате подсчетов получается, что второе итоговое значение имеет три знака, а не два. Допустим, у нас получились числа 12 и 345. В этом случае нужно сложить вторую и третью цифру так, чтобы получилось 1545.

Это основные методы устного умножения. Но можно ли их назвать простыми? Несмотря на то, что при усердных тренировках удастся освоить любой из этих подходов, все же они будут требовать хорошей памяти и высокой концентрации. К тому же, не всегда допустимо проводить операции с многозначными числами с помощью данных методов. Лучше постараться найти для себя другие, более простые способы счета.

Быстрое умножение в уме больших чисел

Математики всех времен искали простые методы быстрого устного счета. Умножение и деление, в отличие от сложения и вычитания, являются более сложными операциями. Поэтому производить такие подсчеты в уме без должной подготовки сложно, тем более когда речь идет о многозначных числах. Проблема устного умножения в том, что не существует какого-либо универсального способа, который бы подходил вне зависимости от ситуации.

Мозг обычного человека не способен работать также быстро, как калькулятор. Мы склонны терять концентрацию, сбиваться, забывать результаты промежуточных операций. Поэтому стандартные способы устного умножения мало пригодны для повседневных задач. Они скорее являются хорошей разминкой для мозга, чем удобным инструментом. Но что делать, если быстро считать без подручных средств все же хочется?

Благодаря интернету можно найти немало информации по этому вопросу. Сегодня существует множество методик, позволяющих научиться складывать, вычитать, умножать и даже делить с моментальной скоростью. Но самым популярным направлением устного счета является ментальная арифметика. Ее неоспоримым плюсом является то, что она дается детям даже легче, чем взрослым.

Лучший способ научиться устному счету

Ментальная арифметика – это не только уникальный способ счета без подручных средств. В основе этой методики лежит равнозначное развитие как левого полушария мозга, отвечающего за логику и анализ, так и правого, которое контролирует работу воображения и фантазии. Несмотря на то, что освоить ментальную арифметику может любой желающий, она все же больше подходит для изучения в раннем возрасте. Именно в детстве можно приобрести навыки, которые не забудутся со временем и сохранятся на всю жизнь.

Обучение ментальной арифметике – длительный процесс, который требует усидчивости и нацеленности на результат. Пройдет немало времени, пока ребенок сможет полностью освоить программу и научиться не только складывать и вычитать, но и умножать и делить многозначные числа. Родителям не всегда удается контролировать периодичность занятий своего ребенка, а также следить за тем, чтобы он выполнял все необходимые упражнения. Этим обусловлен рост популярности групповых занятий ментальной арифметикой в центрах дополнительного развития детей.

Ученики, обучающиеся по этому направлению, сначала осваивают вычисления на древних счетах – абакусе. Когда базовые навыки закрепятся, наступает время для перехода к следующему, более сложному этапу. Теперь ученик постепенно привыкает представлять абакус в своем воображении и производить подсчеты уже на нем. Именно так и удается развить навык быстрого счета.

Благодаря занятиям ментальной арифметикой ребенок повышает успеваемость в школе, ведь теперь ему доступны не только простые вычисления в уме, но и быстрое умножение и деление. Количество времени, которое он тратит на выполнение домашних заданий, также сокращается. Так удается добиться большей продуктивности образовательного процесса в школе и дома. Навыки, приобретенные благодаря ментальной арифметике, сохранятся навсегда, что очень пригодится во взрослой жизни.

Источник

Как быстро считать в уме: приемы устного счета больших чисел

• 12 января 2021 г.
• 15 минут
• 279 402
• 9

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

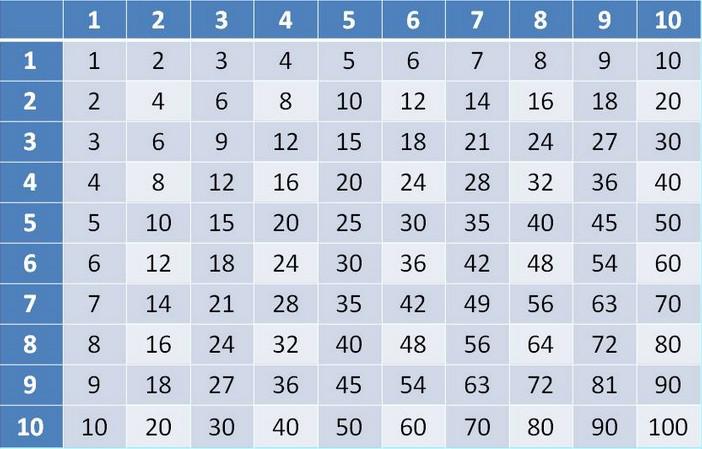
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник