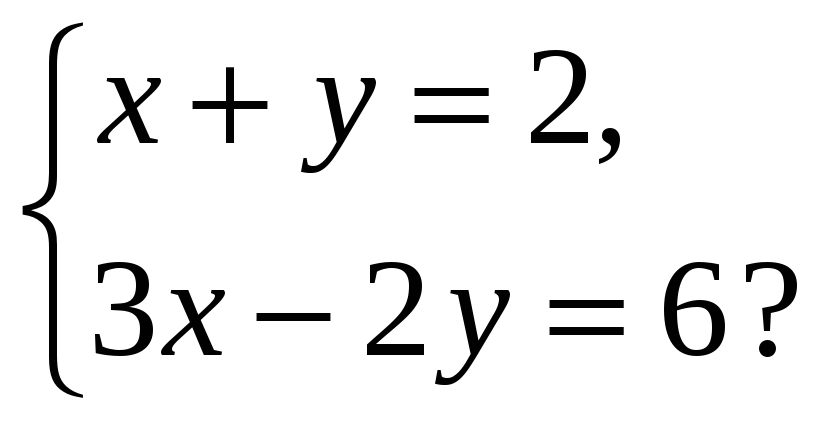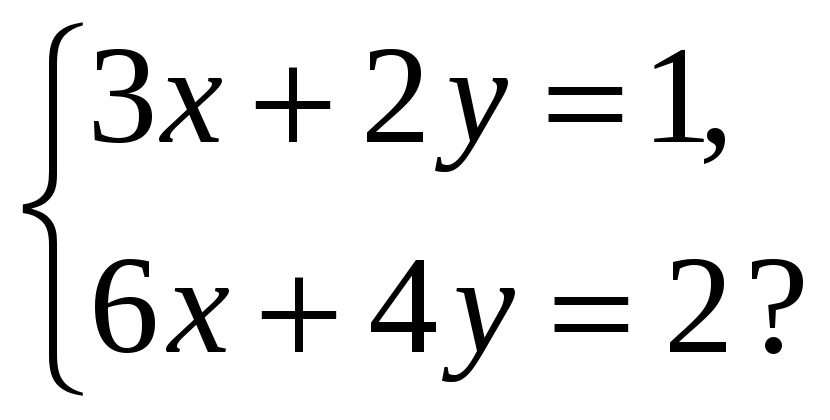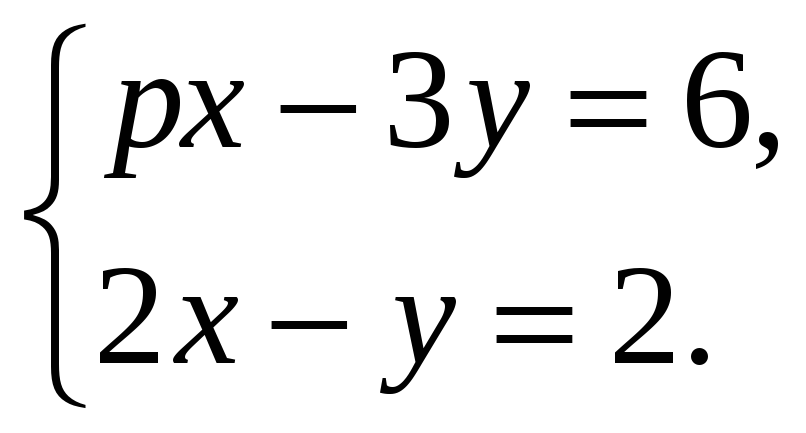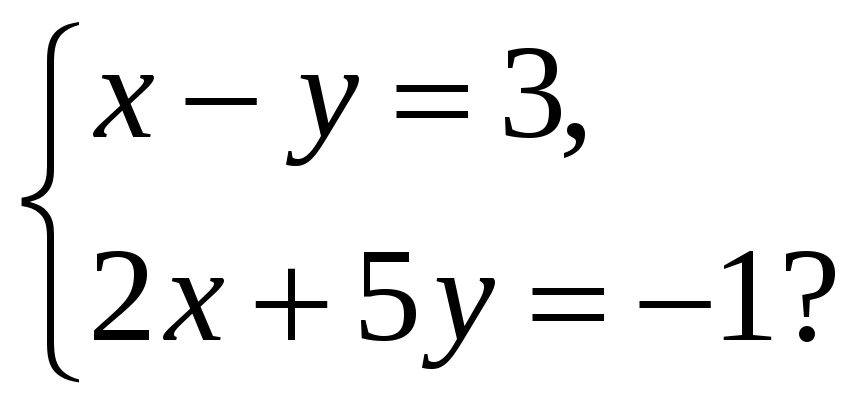- Проверочная работа по теме Графический способ решения СЛУ 7 класс
- Просмотр содержимого документа «Проверочная работа по теме Графический способ решения СЛУ 7 класс»
- Самостоятельные работы по алгебре за 7 класс
- Выберите документ из архива для просмотра:
- Самостоятельные и контрольные работы по алгебре 7 класс
Проверочная работа по теме Графический способ решения СЛУ 7 класс

Проверочная работа по теме Графический способ решения СЛУ 7 класс
Просмотр содержимого документа
«Проверочная работа по теме Графический способ решения СЛУ 7 класс»
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 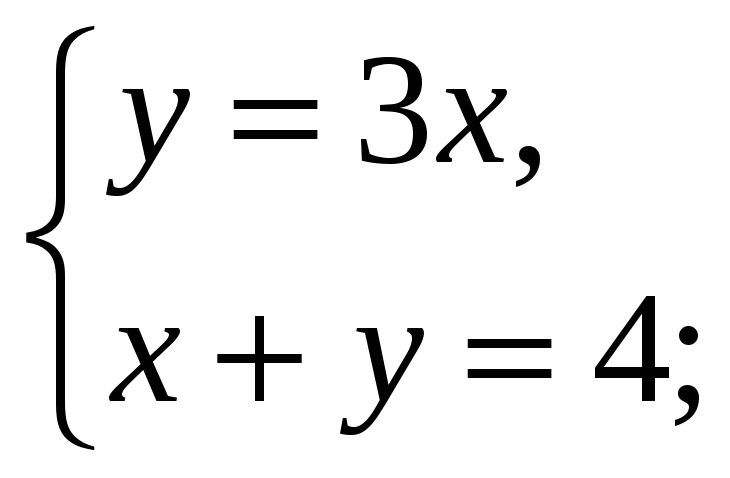
3. Сколько решений имеет система уравнений
а) 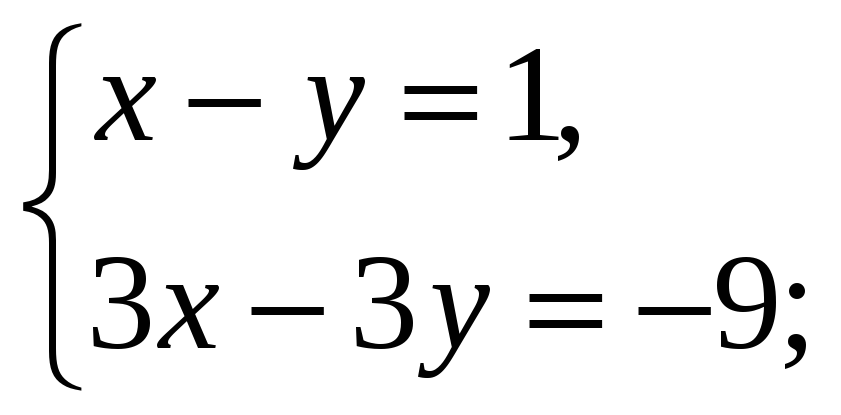
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 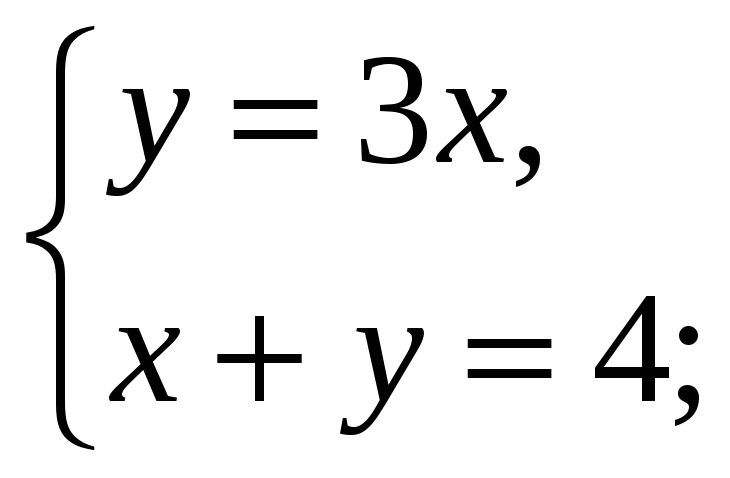
3. Сколько решений имеет система уравнений
а) 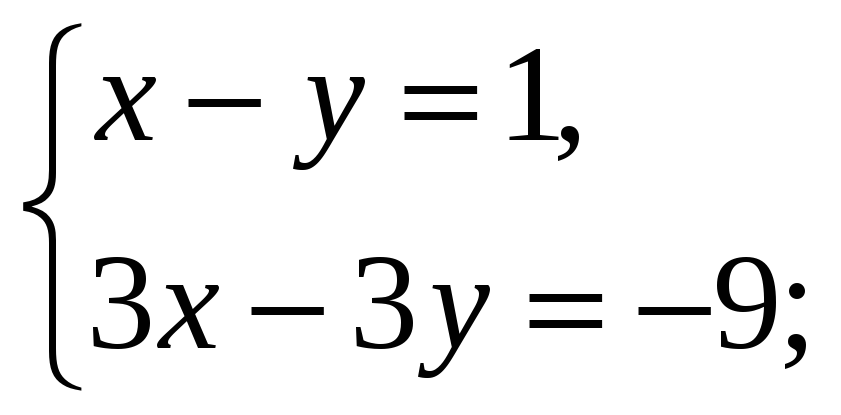
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 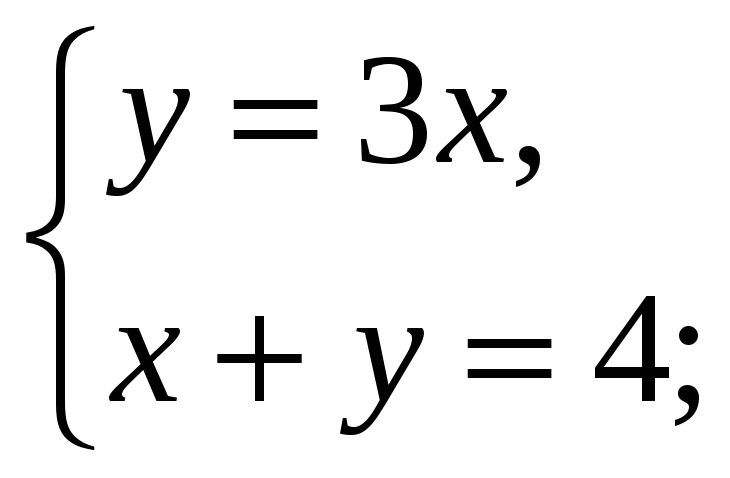
3. Сколько решений имеет система уравнений
а) 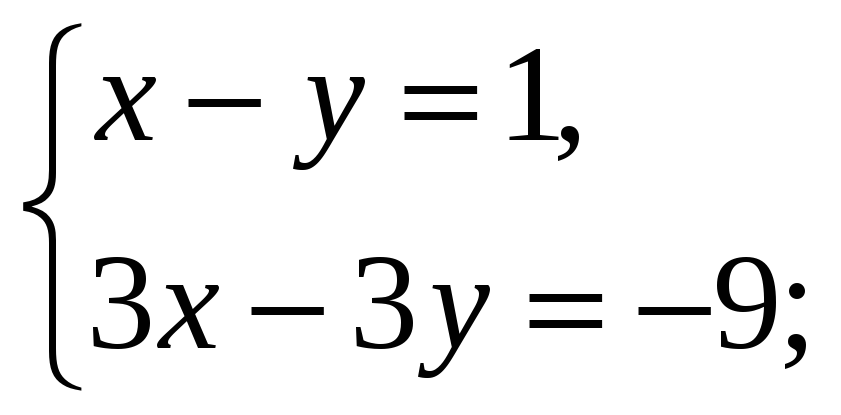
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 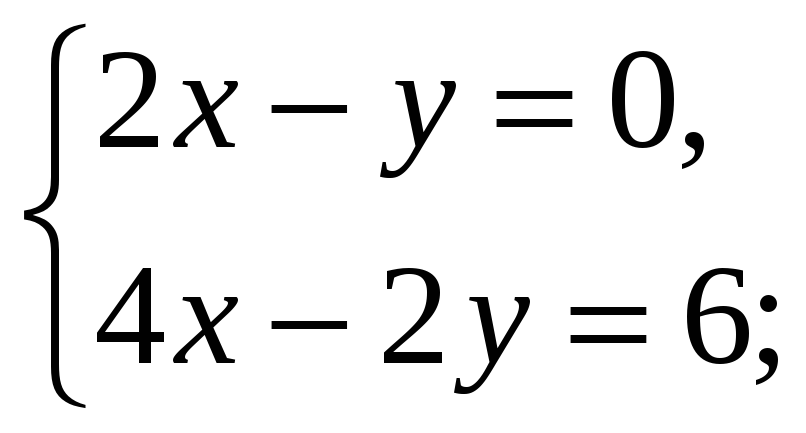
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 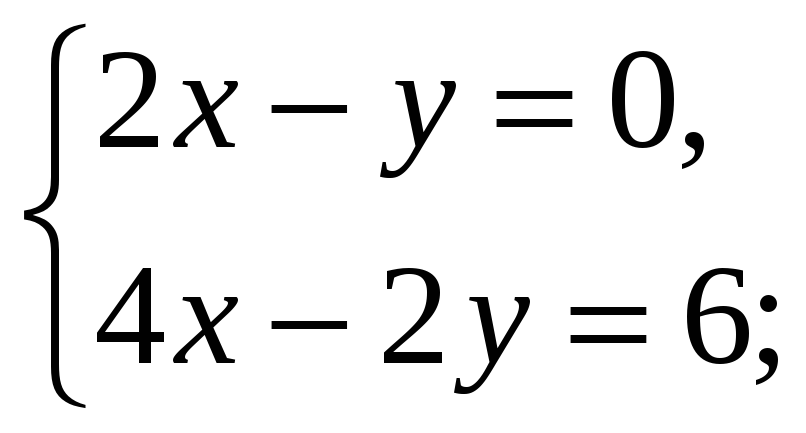
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 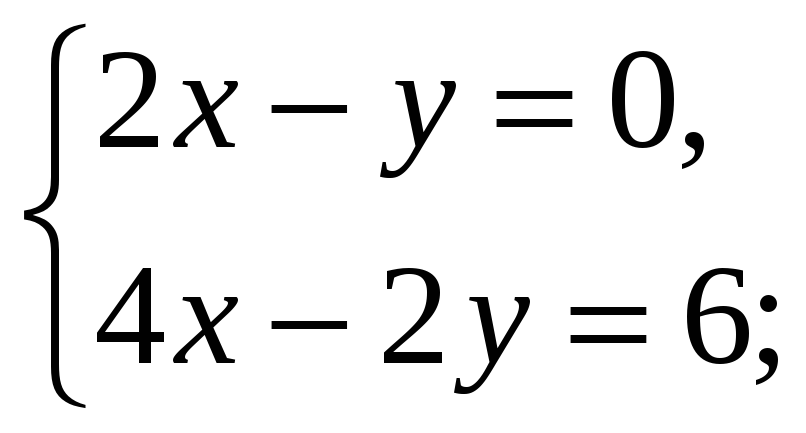
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
Источник
Самостоятельные работы по алгебре за 7 класс
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Самостоятельная работа №1.docx
7 КЛАСС
АЛГЕБРА
____________________________________________________________________________
Самостоятельная работа по теме: «Выражения и тождества»
а) 50,2 – 4,37; в) –4 

б) 

2. Сравните значение выражений:
а) 0,15 × 24 и 


3. Упростите выражение и найдите его значение:
а) (5х – 3) – (2 – 7х) при х = 0,5;
б) у – (2у + 7) – 2(3 – у) + 13 при у = 0,2.
4. На пакете кефира написано, что в кефире содержится 1,5% жира, 3,3% белка и 2,9% углеводов. Какое количество каждого из этих веществ содержится в стакане (250 г) кефира?
а) 51,2 – 5,37; в) –3 

б) 

2. Сравните значение выражений:
а) 0,15 × 22 и 


3. Упростите выражение и найдите его значение:
а) (4х – 8) – (3 – 5х) при х = 1,5;
б) у – (3у – 4) – (4 –5у) –3у при у = 0,3.
4. На пакете кефира написано, что в кефире содержится 1,5% жира, 3,3% белка и 2,9% углеводов. Какое количество каждого из этих веществ содержится в чашке (300 г) кефира?
Источник
Самостоятельные и контрольные работы по алгебре 7 класс
Выбранный для просмотра документ гр. способ реш систем.doc
Самостоятельная работа по теме А — 7
«Графический способ решения систем уравнений»
1 вариант 2 вариант
Р
2х – у = — 6 2) х + у = — 10 1) 3х – у = 10 2) х + у = — 6
3х + у = 1 у = х 4х + у = 4 у = х
Самостоятельная работа по теме А — 7
«Графический способ решения систем уравнений»
1 вариант 2 вариант
Р
1
3х + у = 1 у = х 4х + у = 4 у = х
Самостоятельная работа по теме А — 7
«Графический способ решения систем уравнений»
1 вариант 2 вариант
Р
1
3х + у = 1 у = х 4х + у = 4 у = х
Самостоятельная работа по теме А — 7
«Графический способ решения систем уравнений»
1 вариант 2 вариант
Р
2х – у = — 6 2) х + у = — 10 1) 3х – у = 10 2) х + у = — 6
3х + у = 1 у = х 4х + у = 4 у = х
Самостоятельная работа по теме А — 7
«Графический способ решения систем уравнений»
1 вариант 2 вариант
Р
2х – у = — 6 2) х + у = — 10 1) 3х – у = 10 2) х + у = — 6
3х + у = 1 у = х 4х + у = 4 у = х
Самостоятельная работа по теме А — 7
«Графический способ решения систем уравнений»
1 вариант 2 вариант
Р
2х – у = — 6 2) х + у = — 10 1) 3х – у = 10 2) х + у = — 6
3х + у = 1 у = х 4х + у = 4 у = х
Выбранный для просмотра документ итог. к. р..doc
Экзаменационная контрольная работа по алгебре в 7 классе.
1 вариант 2 вариант
1. Решить уравнение:
3х – 2 ( х + 8 ) = 5х – 4 4 х – 2 ( х + 4 ) = 4 х + 2
2. Упростить выражение:
( а – 3 ) 2 – ( а – 1 ) ( а + 9 ) ( а + 5 ) 2 – ( а + 6 ) ( а + 2 )
3. Разложить на множители:
а) 3ас + 6 а 2 б) 9 х 2 – 25 а) 12ху + 4 у 2 б) 16 х 2 – 49
4. Построить график функции
у = — 4 х + 5 у = 5 х – 4
Определите, принадлежит ли графику функции точка
А ( — 12; — 23) В ( — 9; 49)
5. Упростить выражение:

6. Решить задачу:
У
26 рублей. Другой ученик за такие же 2 тетради 4 детских пальто. Сколько метров ткани
и 3 карандаша заплатил 14 рублей. Сколько стоила необходимо для пошива одного мужского
тетрадь и сколько стоил карандаш? и одного детского пальто, если из 16 м той
же ткани можно сшить 2 мужских и 5
Экзаменационная контрольная работа по алгебре в 7 классе.
1 вариант 2 вариант
1. Решить уравнение:
3х – 2 ( х + 8 ) = 5х – 4 4 х – 2 ( х + 4 ) = 4 х + 2
2. Упростить выражение:
( а – 3 ) 2 – ( а – 1 ) ( а + 9 ) ( а + 5 ) 2 – ( а + 6 ) ( а + 2 )
3. Разложить на множители:
а) 3ас + 6 а 2 б) 9 х 2 – 25 а) 12ху + 4 у 2 б) 16 х 2 – 49
4. Построить график функции
у = — 4 х + 5 у = 5 х – 4
Определите, принадлежит ли графику функции точка
А ( — 12; — 23) В ( — 9; 49)
5. Упростить выражение:

6. Решить задачу:
У
26 рублей. Другой ученик за такие же 2 тетради 4 детских пальто. Сколько метров ткани
и 3 карандаша заплатил 14 рублей. Сколько стоила необходимо для пошива одного мужского
тетрадь и сколько стоил карандаш? и одного детского пальто, если из 16 м той
же ткани можно сшить 2 мужских и 5
Выбранный для просмотра документ к. р. 7 кл. алг. дроби.doc
Контрольная работа А — 7
по теме «Сложение и вычитание алгебраических дробей»
1 вариант 2 вариант
1. Сократить дроби:
1) 




4) 
2. Выполнить действия:
1



3) 


3. Упростить выражение:
4. Сократить дробь и найти её значение:



Контрольная работа А — 7
по теме «Сложение и вычитание алгебраических дробей»
1 вариант 2 вариант
1. Сократить дроби:
1) 




4) 
2. Выполнить действия:
1



3) 


3. Упростить выражение:
4. Сократить дробь и найти её значение:



Выбранный для просмотра документ к. р. 7 сиситемы.doc
Контрольная работа по теме «Системы уравнений»
1 вариант 2 вариант.
1

х – 3 у = 10 х + 4 у = 7
2
5 х – 2 у = — 7 3 х – 5 у = 9
2 х + 3 у = — 18 2 х + 3 у = — 13
3
х

3 х – у = 1 2 х – у = 2
4
2 ( х + у ) – 3 ( х – у ) = 4 5 ( 3 х + у ) – 8 ( х – 6 у ) = 20
5 ( х + у ) – 7 ( х – у ) = 2 6 ( х – 10 у) – 13 ( х – у ) = 52
Контрольная работа по теме «Системы уравнений»
1 вариант 2 вариант.
1

х – 3 у = 10 х + 4 у = 7
2
5 х – 2 у = — 7 3 х – 5 у = 9
2 х + 3 у = — 18 2 х + 3 у = — 13
3
х

3 х – у = 1 2 х – у = 2
4
2 ( х + у ) – 3 ( х – у ) = 4 5 ( 3 х + у ) – 8 ( х – 6 у ) = 20
5 ( х + у ) – 7 ( х – у ) = 2 6 ( х – 10 у) – 13 ( х – у ) = 52
Контрольная работа по теме «Системы уравнений»
1 вариант 2 вариант.
1

х – 3 у = 10 х + 4 у = 7
2
5 х – 2 у = — 7 3 х – 5 у = 9
2 х + 3 у = — 18 2 х + 3 у = — 13
3
х

3 х – у = 1 2 х – у = 2
4
2 ( х + у ) – 3 ( х – у ) = 4 5 ( 3 х + у ) – 8 ( х – 6 у ) = 20
5 ( х + у ) – 7 ( х – у ) = 2 6 ( х – 10 у) – 13 ( х – у ) = 52
Выбранный для просмотра документ к. р. №1 числ и алг выр.doc
Контрольная работа № 1 по теме А — 7
1 вариант 2 вариант
1

2. Найти значение выражения




3. Упростить выражения:
1
2) 5 ( 2 а – 3 ) + 10 2) 2 ( 5 а – 3 ) + 11
3) 8 а – ( 11 – 6а ) 3) 13 – ( 5х – 7 )
4) 3х – ( 4 а – 6х ) + ( — 5 а – 9 х ) 4) 7у + ( — 8 а – 3 у ) – ( 5 а + у )
5) 4 ( 2 х – 7 ) – 6 ( 1 + 3х ) 5) 8 ( 3 а – 4 ) – 5 ( 2 + 5 а )
6) 0,6 ( с – 3 х ) – 1,3 ( 2 х – с) 6) 0,4 ( с + 3 х ) – 1,8 ( 2 х + с )
7) 3,7х — у – ( 4,5у + х ) – 3 ( 0,9 х – 1,1 у) 7) 2,8 а – 2 с + ( 3,3 а – 1,4 с ) – 2 ( а — 1,7 с)
4


Контрольная работа № 1 по теме А — 7
1 вариант 2 вариант
1

2. Найти значение выражения




3. Упростить выражения:
1
2) 5 ( 2 а – 3 ) + 10 2) 2 ( 5 а – 3 ) + 11
3) 8 а – ( 11 – 6а ) 3) 13 – ( 5х – 7 )
4) 3х – ( 4 а – 6х ) + ( — 5 а – 9 х ) 4) 7у + ( — 8 а – 3 у ) – ( 5 а + у )
5) 4 ( 2 х – 7 ) – 6 ( 1 + 3х ) 5) 8 ( 3 а – 4 ) – 5 ( 2 + 5 а )
6) 0,6 ( с – 3 х ) – 1,3 ( 2 х – с) 6) 0,4 ( с + 3 х ) – 1,8 ( 2 х + с )
7) 3,7х — у – ( 4,5у + х ) – 3 ( 0,9 х – 1,1 у) 7) 2,8 а – 2 с + ( 3,3 а – 1,4 с ) – 2 ( а — 1,7 с)
4


Выбранный для просмотра документ к.р. 1 7 кл алг выражения мордкович.docx
Контрольная работа № 1 по теме «Алгебраические выражения»
1 вариант 2 вариант
Упростите алгебраическое выражение и найдите его значение
4 ( 4с – 3 ) – ( 10с + 8 ) при с = 0,6 3 ( 5 – 4 а) – ( 9 а – 7 ) при а = — 0,1
а) 7х + 1,5 = 10х – 3 а) 6х – 7 = 15 + 2х
б) 5 ( 2х – 3) – 33 = 4 ( 3х – 5) б) 7 ( 3х – 1) + 5х = 5 ( 6х – 11)
в) 2х + 4 3х – 1 в) 5х + 1 4х – 3
Контрольная работа № 1 по теме «Алгебраические выражения»
1 вариант 2 вариант
Упростите алгебраическое выражение и найдите его значение
4 ( 4с – 3 ) – ( 10с + 8 ) при с = 0,6 3 ( 5 – 4 а) – ( 9 а – 7 ) при а = — 0,1
а) 7х + 1,5 = 10х – 3 а) 6х – 7 = 15 + 2х
б) 5 ( 2х – 3) – 33 = 4 ( 3х – 5) б) 7 ( 3х – 1) + 5х = 5 ( 6х – 11)
в) 2х + 4 3х – 1 в) 5х + 1 4х – 3
Контрольная работа № 1 по теме «Алгебраические выражения»
1 вариант 2 вариант
Упростите алгебраическое выражение и найдите его значение
4 ( 4с – 3 ) – ( 10с + 8 ) при с = 0,6 3 ( 5 – 4 а) – ( 9 а – 7 ) при а = — 0,1
а) 7х + 1,5 = 10х – 3 а) 6х – 7 = 15 + 2х
б) 5 ( 2х – 3) – 33 = 4 ( 3х – 5) б) 7 ( 3х – 1) + 5х = 5 ( 6х – 11)
в) 2х + 4 3х – 1 в) 5х + 1 4х – 3
Выбранный для просмотра документ к.р. 7 кл алг др..doc
Контрольная работа по теме
«Совместные действия с алгебраическими дробями»
1.Выполнить действия: 1) 


2. Упростить выражение:
3. Упростить выражение и найти его значение: 
4
Контрольная работа по теме
«Совместные действия с алгебраическими дробями»
1.Выполнить действия: 1) 


2. Упростить выражение:
3. Упростить выражение и найти его значение: 
4. Упростить выражение:
Контрольная работа по теме
«Совместные действия с алгебраическими дробями»
1. Выполнить действия: 1) 


2. Упростить выражение:
3. Упростить выражение и найти его значение: 
4. Упростить выражение:
Контрольная работа по теме
«Совместные действия с алгебраическими дробями»
1.Выполнить действия: 1) 


2. Упростить выражение:
3. Упростить выражение и найти его значение: 
4. Упростить выражение:
Выбранный для просмотра документ коорд. плоскость.doc
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1
С( — 4 ; 3 ) и Е ( 3 ; — 1 ) А ( 3 ; 4 ) и В ( — 5 ; — 1 )
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А 
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
О
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1. Постройте в координатной плоскости прямую, проходящую через точки
С
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А 
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
О
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1
С( — 4 ; 3 ) и Е ( 3 ; — 1 ) А ( 3 ; 4 ) и В ( — 5 ; — 1 )
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А 
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
О
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1. Постройте в координатной плоскости прямую, проходящую через точки
С
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А 
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
О
Выбранный для просмотра документ лин. функция.doc
Самостоятельная работа по теме А — 7
«Линейная функция и ее график»
1 вариант 2 вариант
1. Построить график функции:
1) у = 4 х – 6 2) у = — 7 х 1) у = 3 х – 8 2) у = — 6 х
2. Не выполняя построения графика функции
у = — 5 х + 11 у = — 4 х + 13
выяснить проходит ли он через точку
А ( 8 ; 29 ) , В ( — 0,9 ; 15,5) , С ( — 19 ; — 84 ) А ( 9 ; 23 ) , В ( — 0,8 ; 16,2) , С ( — 15 ; — 47 )
3. Постройте в одной системе координат графики функций и укажите координаты точки их пересечения:
у = 0,5 х + 1 и у = — х + 4 у = 0,5 х – 1 и у = — х – 4
Самостоятельная работа по теме А — 7
«Линейная функция и ее график»
1 вариант 2 вариант
1. Построить график функции:
1) у = 4 х – 6 2) у = — 7 х 1) у = 3 х – 8 2) у = — 6 х
2. Не выполняя построения графика функции
у = — 5 х + 11 у = — 4 х + 13
выяснить проходит ли он через точку
А ( 8 ; 29 ) , В ( — 0,9 ; 15,5) , С ( — 19 ; — 84 ) А ( 9 ; 23 ) , В ( — 0,8 ; 16,2) , С ( — 15 ; — 47 )
3. Постройте в одной системе координат графики функций и укажите координаты точки их пересечения:
у = 0,5 х + 1 и у = — х + 4 у = 0,5 х – 1 и у = — х – 4
Самостоятельная работа по теме А — 7
«Линейная функция и ее график»
1 вариант 2 вариант
1. Построить график функции:
1) у = 4 х – 6 2) у = — 7 х 1) у = 3 х – 8 2) у = — 6 х
2. Не выполняя построения графика функции
у = — 5 х + 11 у = — 4 х + 13
выяснить проходит ли он через точку
А ( 8 ; 29 ) , В ( — 0,9 ; 15,5) , С ( — 19 ; — 84 ) А ( 9 ; 23 ) , В ( — 0,8 ; 16,2) , С ( — 15 ; — 47 )
3. Постройте в одной системе координат графики функций и укажите координаты точки их пересечения:
у = 0,5 х + 1 и у = — х + 4 у = 0,5 х – 1 и у = — х – 4
Самостоятельная работа по теме А — 7
«Линейная функция и ее график»
1 вариант 2 вариант
1. Построить график функции:
1) у = 4 х – 6 2) у = — 7 х 1) у = 3 х – 8 2) у = — 6 х
2. Не выполняя построения графика функции
у = — 5 х + 11 у = — 4 х + 13
выяснить проходит ли он через точку
А ( 8 ; 29 ) , В ( — 0,9 ; 15,5) , С ( — 19 ; — 84 ) А ( 9 ; 23 ) , В ( — 0,8 ; 16,2) , С ( — 15 ; — 47 )
3. Постройте в одной системе координат графики функций и укажите координаты точки их пересечения:
у = 0,5 х + 1 и у = — х + 4 у = 0,5 х – 1 и у = — х – 4
Выбранный для просмотра документ линейная функция.doc
Контрольная работа по теме А — 7
«Линейная функция и ее график»
1. Функция задана формулой у = 4х – 20. Определите:
а) чему равно значение у при х = — 2,5
б) при каком значении х значение у равно 4
в) проходит ли график функции через точку С ( — 2 ; — 28 )
2. Постройте график функции у = 2 х – 6 . Укажите с помощью графика, чему равно значение у при х = 1,5.
3. В одной и той же системе координат постройте графики функций у = — 3 х – 7 и у = — 1. Найти координаты точки пересечения.
4. Найти значение k , если известно, что график функции у = k х + 9 проходит через точку
А ( — 4 ; 1). Постройте график полученной функции.
1. Функция задана формулой у = — 4х – 18. Определите:
а) чему равно значение у при х = 2,5
б) при каком значении х значение у равно 2
в) проходит ли график функции через точку К ( 2 ; — 20 )
2. Постройте график функции у = — 2 х – 6 . Укажите с помощью графика, чему равно значение у при х = — 2.
3. В одной и той же системе координат постройте графики функций у = — 5 х + 7 и у = 1. Найти координаты точки пересечения.
4. Найти значение k , если известно, что график функции у = k х + 15 проходит через точку
Е ( — 6 ; 3). Постройте график полученной функции.
Контрольная работа по теме А — 7
«Линейная функция и ее график»
1. Функция задана формулой у = 4х – 20. Определите:
а) чему равно значение у при х = — 2,5
б) при каком значении х значение у равно 4
в) проходит ли график функции через точку С ( — 2 ; — 28 )
2. Постройте график функции у = 2 х – 6 . Укажите с помощью графика, чему равно значение у при х = 1,5.
3. В одной и той же системе координат постройте графики функций у = — 3 х – 7 и у = — 1. Найти координаты точки пересечения.
4. Найти значение k , если известно, что график функции у = k х + 9 проходит через точку
А ( — 4 ; 1). Постройте график полученной функции.
1. Функция задана формулой у = — 4х – 18. Определите:
а) чему равно значение у при х = 2,5
б) при каком значении х значение у равно 2
в) проходит ли график функции через точку К ( 2 ; — 20 )
2. Постройте график функции у = — 2 х – 6 . Укажите с помощью графика, чему равно значение у при х = — 2.
3. В одной и той же системе координат постройте графики функций у = — 5 х + 7 и у = 1. Найти координаты точки пересечения.
4. Найти значение k , если известно, что график функции у = k х + 15 проходит через точку
Е ( — 6 ; 3). Постройте график полученной функции.
Выбранный для просмотра документ прив подобных.doc
Самостоятельная работа по теме А — 7
«Приведение подобных слагаемых»
1 вариант 2 вариант
1. Привести подобные слагаемые:
1
2) – 1,3 а – 4,7 + а + 8 2) — 6,1 х + 3 – х – 3,9
3) 8 х – 7 а – 6,9 – 7 а – 8 х +3,7 3) 7 х – 5,4 + 3,8 – 7 х – 5 у – 5 у
4) 5 ( 4 х – 7 ) + 3 ( 3 – 8 х ) 4) 4 ( 3 у – 8 ) + 6 ( у – 2)
5) 0,2 ( 3 а – 2 ) – 1,5 ( 2 а + 3) 5) 0,3 ( 4 х – 3 ) – 1,4 ( 3 х + 2)
6) 7 ( 2,1 х + 3,3 у ) + 4 ( 1,2 х – 2,6 у) 6) 6 ( 3,1 а + 2,2 с ) + 3 ( 2,8 а – 1,7 с )
2. Упростить выражение и найти его значение:
1
2) 

Самостоятельная работа по теме А — 7
«Приведение подобных слагаемых»
1 вариант 2 вариант
1. Привести подобные слагаемые:
1
2) – 1,3 а – 4,7 + а + 8 2) — 6,1 х + 3 – х – 3,9
3) 8 х – 7 а – 6,9 – 7 а – 8 х +3,7 3) 7 х – 5,4 + 3,8 – 7 х – 5 у – 5 у
4) 5 ( 4 х – 7 ) + 3 ( 3 – 8 х ) 4) 4 ( 3 у – 8 ) + 6 ( у – 2)
5) 0,2 ( 3 а – 2 ) – 1,5 ( 2 а + 3) 5) 0,3 ( 4 х – 3 ) – 1,4 ( 3 х + 2)
6) 7 ( 2,1 х + 3,3 у ) + 4 ( 1,2 х – 2,6 у) 6) 6 ( 3,1 а + 2,2 с ) + 3 ( 2,8 а – 1,7 с )
2. Упростить выражение и найти его значение:
1
2) 

Самостоятельная работа по теме А — 7
«Приведение подобных слагаемых»
1 вариант 2 вариант
1. Привести подобные слагаемые:
1
2) – 1,3 а – 4,7 + а + 8 2) — 6,1 х + 3 – х – 3,9
3) 8 х – 7 а – 6,9 – 7 а – 8 х +3,7 3) 7 х – 5,4 + 3,8 – 7 х – 5 у – 5 у
4) 5 ( 4 х – 7 ) + 3 ( 3 – 8 х ) 4) 4 ( 3 у – 8 ) + 6 ( у – 2)
5) 0,2 ( 3 а – 2 ) – 1,5 ( 2 а + 3) 5) 0,3 ( 4 х – 3 ) – 1,4 ( 3 х + 2)
6) 7 ( 2,1 х + 3,3 у ) + 4 ( 1,2 х – 2,6 у) 6) 6 ( 3,1 а + 2,2 с ) + 3 ( 2,8 а – 1,7 с )
2. Упростить выражение и найти его значение:
1
2) 

Выбранный для просмотра документ с. р. алг выражения.doc
Самостоятельная работа по теме «Алгебраические выражения»
Вариант 1 Вариант 2
Найти значение алгебраического выражения:
1

2) 




3) 

Самостоятельная работа по теме «Алгебраические выражения»
Вариант 1 Вариант 2
Найти значение алгебраического выражения:
1

2) 




3) 

Самостоятельная работа по теме «Алгебраические выражения»
Вариант 1 Вариант 2
Найти значение алгебраического выражения:
1

2) 




3) 

Самостоятельная работа по теме «Алгебраические выражения»
Вариант 1 Вариант 2
Найти значение алгебраического выражения:
1

2) 




3) 

Выбранный для просмотра документ способ сложения.doc
Самостоятельная работа по теме «Способ сложения» А – 7
1 вариант 2 вариант
Р
2 
3 х + 4 у = 24 2 х + 5 у = 8
2 – 3 х = 2 ( 1 – у ) 2) 2 – 4 у = 3 ( х – 2 )
4 ( х + у ) = х – 1,5 2 ( х + у ) = 5 у + 2,5







Самостоятельная работа по теме «Способ сложения» А – 7
1 вариант 2 вариант
Р
2 
3 х + 4 у = 24 2 х + 5 у = 8
2 – 3 х = 2 ( 1 – у ) 2) 2 – 4 у = 3 ( х – 2 )
4 ( х + у ) = х – 1,5 2 ( х + у ) = 5 у + 2,5







Самостоятельная работа по теме «Способ сложения» А – 7
1 вариант 2 вариант
Р
2 
3 х + 4 у = 24 2 х + 5 у = 8
2 – 3 х = 2 ( 1 – у ) 2) 2 – 4 у = 3 ( х – 2 )
4 ( х + у ) = х – 1,5 2 ( х + у ) = 5 у + 2,5







Выбранный для просмотра документ умнож мн на одн.doc
Самостоятельная работа по теме
«Умножение многочлена на одночлен»
1. Найти произведение многочлена на одночлен:
1) 5х 3 ( 4х — 7) 2) 8ас ( 3а + 2с 2 – 1) 3) 11х (2х – 3у – ху) 4) 4х 2 у ( 3х — 5у ) 2. Упростить выражение:
1) 7(2х – 5) – 11(1 + 3х) 2) 8у ( 2у 2 + 5) – 3у (7 – 4у 2 )
3. Найти значение выражения:
3а 2 ( 5а – 3с) – 5а ( 3а 2 + ас) при а = — 1, с = 2
1. Найти произведение многочлена на одночлен:
1) 4х 2 ( 7х — 9) 2) 5ас ( 9а — 8с 2 – 2) 3) 13х (х – 4у + 2ху) 4) 6х 3 у ( 2х + 7у )
2. Упростить выражение:
1) 6(5х – 7) – 10(2 + 5х) 2) 3у ( 9у 2 — 4) – 5у (6 + 2у 2 )
3. Найти значение выражения:
2а 2 ( 9а – 7с) – 9а ( 2а 2 + ас) при а = — 2, с = 5
Самостоятельная работа по теме
«Умножение многочлена на одночлен»
1. Найти произведение многочлена на одночлен:
1) 5х 3 ( 4х — 7) 2) 8ас ( 3а + 2с 2 – 1) 3) 11х (2х – 3у – ху) 4) 4х 2 у ( 3х — 5у ) 2. Упростить выражение:
1) 7(2х – 5) – 11(1 + 3х) 2) 8у ( 2у 2 + 5) – 3у (7 – 4у 2 )
3. Найти значение выражения:
3а 2 ( 5а – 3с) – 5а ( 3а 2 + ас) при а = — 1, с = 2
1. Найти произведение многочлена на одночлен:
1) 4х 2 ( 7х — 9) 2) 5ас ( 9а — 8с 2 – 2) 3) 13х (х – 4у + 2ху) 4) 6х 3 у ( 2х + 7у )
2. Упростить выражение:
1) 6(5х – 7) – 10(2 + 5х) 2) 3у ( 9у 2 — 4) – 5у (6 + 2у 2 )
3. Найти значение выражения:
2а 2 ( 9а – 7с) – 9а ( 2а 2 + ас) при а = — 2, с = 5
Самостоятельная работа по теме
«Умножение многочлена на одночлен»
1. Найти произведение многочлена на одночлен:
1) 5х 3 ( 4х — 7) 2) 8ас ( 3а + 2с 2 – 1) 3) 11х (2х – 3у – ху) 4) 4х 2 у ( 3х — 5у ) 2. Упростить выражение:
1) 7(2х – 5) – 11(1 + 3х) 2) 8у ( 2у 2 + 5) – 3у (7 – 4у 2 )
3. Найти значение выражения:
3а 2 ( 5а – 3с) – 5а ( 3а 2 + ас) при а = — 1, с = 2
1. Найти произведение многочлена на одночлен:
1) 4х 2 ( 7х — 9) 2) 5ас ( 9а — 8с 2 – 2) 3) 13х (х – 4у + 2ху) 4) 6х 3 у ( 2х + 7у )
2. Упростить выражение:
1) 6(5х – 7) – 10(2 + 5х) 2) 3у ( 9у 2 — 4) – 5у (6 + 2у 2 )
3. Найти значение выражения:
2а 2 ( 9а – 7с) – 9а ( 2а 2 + ас) при а = — 2, с = 5
Выбранный для просмотра документ формулы сокр умн.doc
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1. Упростить выражение:
1) (3х – 1) 2 2) (2х + 5у) 2 3) (6х – 7)(6х + 7) 1) (8а – 3) 2 2) (4а + 7 b ) 2 3) (2х – 3у)(2х + 3у)
4) (2х + 5) 3 5) ( 1 – 4у) 3 4) (5х – 2) 3 5) ( 2 – 4х ) 3
2. Разложить на множители:
1) 81х 2 – 25 2) 16х 4 – 9у 6 3) 49х 2 + 14х +1 1) 36а 2 – 49 2) 9а 6 – 4 b 4 3) 64х 2 – 16х +1
4) 27а 3 + 8 5) 64х 6 — 125 4) 8х 3 + 125 5) 64а 6 – 27

«Формулы сокращенного умножения»
1 вариант 2 вариант
1. Упростить выражение:
1) (3х – 1) 2 2) (2х + 5у) 2 3) (6х – 7)(6х + 7) 1) (8а – 3) 2 2) (4а + 7 b ) 2 3) (2х – 3у)(2х + 3у)
4) (2х + 5) 3 5) ( 1 – 4у) 3 4) (5х – 2) 3 5) ( 2 – 4х ) 3
2. Разложить на множители:
1) 81х 2 – 25 2) 16х 4 – 9у 6 3) 49х 2 + 14х +1 1) 36а 2 – 49 2) 9а 6 – 4 b 4 3) 64х 2 – 16х +1
4) 27а 3 + 8 5) 64х 6 — 125 4) 8х 3 + 125 5) 64а 6 – 27
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1. Упростить выражение:
1) (3х – 1) 2 2) (2х + 5у) 2 3) (6х – 7)(6х + 7) 1) (8а – 3) 2 2) (4а + 7 b ) 2 3) (2х – 3у)(2х + 3у)
4) (2х + 5) 3 5) ( 1 – 4у) 3 4) (5х – 2) 3 5) ( 2 – 4х ) 3
2. Разложить на множители:
1) 81х 2 – 25 2) 16х 4 – 9у 6 3) 49х 2 + 14х +1 1) 36а 2 – 49 2) 9а 6 – 4 b 4 3) 64х 2 – 16х +1
4) 27а 3 + 8 5) 64х 6 — 125 4) 8х 3 + 125 5) 64а 6 – 27
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1. Упростить выражение:
1) (3х – 1) 2 2) (2х + 5у) 2 3) (6х – 7)(6х + 7) 1) (8а – 3) 2 2) (4а + 7 b ) 2 3) (2х – 3у)(2х + 3у)
4) (2х + 5) 3 5) ( 1 – 4у) 3 4) (5х – 2) 3 5) ( 2 – 4х ) 3
2. Разложить на множители:
1) 81х 2 – 25 2) 16х 4 – 9у 6 3) 49х 2 + 14х +1 1) 36а 2 – 49 2) 9а 6 – 4 b 4 3) 64х 2 – 16х +1
4) 27а 3 + 8 5) 64х 6 — 125 4) 8х 3 + 125 5) 64а 6 – 27
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1. Упростить выражение:
1) (3х – 1) 2 2) (2х + 5у) 2 3) (6х – 7)(6х + 7) 1) (8а – 3) 2 2) (4а + 7 b ) 2 3) (2х – 3у)(2х + 3у)
4) (2х + 5) 3 5) ( 1 – 4у) 3 4) (5х – 2) 3 5) ( 2 – 4х ) 3
2. Разложить на множители:
1) 81х 2 – 25 2) 16х 4 – 9у 6 3) 49х 2 + 14х +1 1) 36а 2 – 49 2) 9а 6 – 4 b 4 3) 64х 2 – 16х +1
4) 27а 3 + 8 5) 64х 6 — 125 4) 8х 3 + 125 5) 64а 6 – 27
Выбранный для просмотра документ формулы сокращенного умножения.doc
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1
1) (х – 7) 2 2) (х – 6)(х + 6) 1) (х + 6) 2 2) (х – 8)(х + 8)
3) (2х 2 + 5) 2 4) (х 2 – 3у 3 ) 2 3) (3х 2 – 4) 2 4) (х 3 + 2у 2 ) 2
5) (8х 2 + 9)(8х 2 – 9) 5) (5х 2 + 1)(5х 2 – 1)
2
1) х 2 – 16х + 64 2) 4х 2 – 12х + 9 1) х 2 + 14х + 49 2) 9х 2 – 12х + 4
3) 25х 2 + 60ху +36у 2 4) х 4 + 8х 2 у 3 +16у 6 3) 64х 2 + 80ху +25у 2 4) х 4 + 18х 2 у 3 +81у 6
5) 9у 2 – 49х 2 6) 16х 4 – 25у 6 5) 4у 2 – 9х 2 6) 36х 4 – 49у 6
3. Упростить выражения:
1
3
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1
1) (х – 7) 2 2) (х – 6)(х + 6) 1) (х + 6) 2 2) (х – 8)(х + 8)
3) (2х 2 + 5) 2 4) (х 2 – 3у 3 ) 2 3) (3х 2 – 4) 2 4) (х 3 + 2у 2 ) 2
5) (8х 2 + 9)(8х 2 – 9) 5) (5х 2 + 1)(5х 2 – 1)
2
1) х 2 – 16х + 64 2) 4х 2 – 12х + 9 1) х 2 + 14х + 49 2) 9х 2 – 12х + 4
3) 25х 2 + 60ху +36у 2 4) х 4 + 8х 2 у 3 +16у 6 3) 64х 2 + 80ху +25у 2 4) х 4 + 18х 2 у 3 +81у 6
5) 9у 2 – 49х 2 6) 16х 4 – 25у 6 5) 4у 2 – 9х 2 6) 36х 4 – 49у 6
3. Упростить выражения:
1
3
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1
1) (х – 7) 2 2) (х – 6)(х + 6) 1) (х + 6) 2 2) (х – 8)(х + 8)
3) (2х 2 + 5) 2 4) (х 2 – 3у 3 ) 2 3) (3х 2 – 4) 2 4) (х 3 + 2у 2 ) 2
5) (8х 2 + 9)(8х 2 – 9) 5) (5х 2 + 1)(5х 2 – 1)
2
1) х 2 – 16х + 64 2) 4х 2 – 12х + 9 1) х 2 + 14х + 49 2) 9х 2 – 12х + 4
3) 25х 2 + 60ху +36у 2 4) х 4 + 8х 2 у 3 +16у 6 3) 64х 2 + 80ху +25у 2 4) х 4 + 18х 2 у 3 +81у 6
5) 9у 2 – 49х 2 6) 16х 4 – 25у 6 5) 4у 2 – 9х 2 6) 36х 4 – 49у 6
3. Упростить выражения:
1
3
Самостоятельная работа по теме
«Формулы сокращенного умножения»
1 вариант 2 вариант
1
1) (х – 7) 2 2) (х – 6)(х + 6) 1) (х + 6) 2 2) (х – 8)(х + 8)
3) (2х 2 + 5) 2 4) (х 2 – 3у 3 ) 2 3) (3х 2 – 4) 2 4) (х 3 + 2у 2 ) 2
5) (8х 2 + 9)(8х 2 – 9) 5) (5х 2 + 1)(5х 2 – 1)
2
1) х 2 – 16х + 64 2) 4х 2 – 12х + 9 1) х 2 + 14х + 49 2) 9х 2 – 12х + 4
3) 25х 2 + 60ху +36у 2 4) х 4 + 8х 2 у 3 +16у 6 3) 64х 2 + 80ху +25у 2 4) х 4 + 18х 2 у 3 +81у 6
5) 9у 2 – 49х 2 6) 16х 4 – 25у 6 5) 4у 2 – 9х 2 6) 36х 4 – 49у 6
3. Упростить выражения:
1
3) (10х + 9) 2 – (10х – 3) ( 10х + 3) 3) (3х + 7) 2 – (3х – 4) ( 3х + 4)
Выбранный для просмотра документ числ и алг выр 7 алг.doc
Выбранный для просмотра документ числовые выражения.doc
Самостоятельная работа по теме «Числовые выражения»
Вариант 1 Вариант 2
1



4) 




2. Найти значение выражения:
1




Самостоятельная работа по теме «Числовые выражения»
Вариант 1 Вариант 2
1



4) 




2. Найти значение выражения:
1




Самостоятельная работа по теме «Числовые выражения»
Вариант 1 Вариант 2
1



4) 




2. Найти значение выражения:
1




Самостоятельная работа по теме «Числовые выражения»
Вариант 1 Вариант 2
1



4) 




2. Найти значение выражения:
1




Самостоятельная работа по теме «Числовые выражения»
Вариант 1 Вариант 2
1



4) 




2. Найти значение выражения:
1




Источник