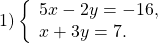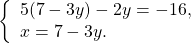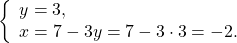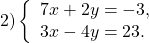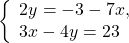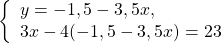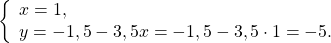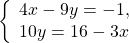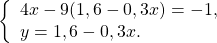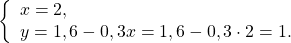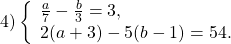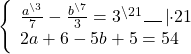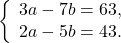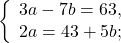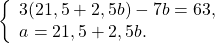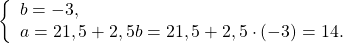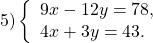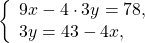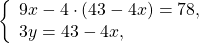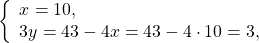С 46 решение систем линейных уравнений способом подстановки ответы

Примеры решения систем линейных уравнений методом подстановки

Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.

В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:

Первое уравнение — уравнение с одной переменной y. Решаем его:

Полученное значение y подставляем в выражение для x:

В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:

Второе уравнение — уравнение с одной переменной x. Решим его:

В выражение для y вместо x подставляем x=1 и находим y:

Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):

Решаем первое уравнение:

Подставляем x=2 и находим y:

Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:

Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:

Решаем первое уравнение системы:

3(21,5 + 2,5b) — 7b = 63

Осталось найти значение a:

Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.

Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.

В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:

Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.

Источник

Решение системы линейных уравнений методом подстановки

Алгоритм решения системы линейных уравнений методом подстановки

1. Из любого уравнения системы выразить одну переменную через другую.
2. Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
3. Решить второе уравнение относительно выраженной переменной.
4. Подставить найденное значение переменной в выражение, полученное на первом шаге.
5. Найти значение второй переменой.
6. Записать ответ в виде упорядоченной пары найденных значений переменных.

Из второго уравнения выражаем y:

Подставляем выражение для y в первое уравнение:

Шаг 3 Решаем первое уравнение:

Подставляем значение x в выражение для y:

В последовательной записи:

$$ <\left\< \begin 3x+y = 5 \\ y-x = 1 \end \right.> \Rightarrow <\left\< \begin 3x+y = 5 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin 3x+(x+1) = 5 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin 4x = 5-1 \\ y = x+1 \end \right.> \Rightarrow $$ $$ \Rightarrow <\left\< \begin x = 1 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 2\end \right.> $$

Примеры

Пример 1. Решите систему уравнений методом подстановки:

$ а) <\left\< \begin 5x-4y = 3 \\ 2x-3y = 4 \end \right.> \Rightarrow <\left\< \begin 5x-4y = 3 \\ x = \frac<3y+4> <2>= 1,5y+2 \end \right.> \Rightarrow <\left\< \begin 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 7,5y+10-4y = 3 \\ x=1,5y+2 \end \right.> \Rightarrow <\left\< \begin 3,5y = -7 \\ x = 1,5y+2 \end \right.> \Rightarrow <\left\< \begin y = -2 \\ x = 1,5y+2 \end \right.> \Rightarrow <\left\< \begin x = -1 \\ y = -2\end \right.> $

$ б) <\left\< \begin 4x-3y = 7 \\ 3x-4y = 0 \end \right.> \Rightarrow <\left\< \begin 4x-3y = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow <\left\< \begin 4x-3\cdot \frac<3> <4>x = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow <\left\< \begin (4- \frac<9><4>)x = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow $

$\Rightarrow <\left\< \begin x = 7 \cdot \frac<4> <7>= 4 \\ y = \frac<3> <4>x = \frac<3> <4>\cdot 4 = 3 \end \right.> \Rightarrow <\left\< \beginx = 4 \\ y = 3 \end \right.> $

$ в) <\left\< \begin 5a-4b = 9 \\ 2a+3b = -1 \end \right.> \Rightarrow <\left\< \begin 5a-4b = 9 \\ a = \frac<-3b-1> <2>= -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin-11,5b = 11,5 \\ a = -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin a = 1 \\ b = -1 \end \right.> $

$ г) <\left\< \begin 7a+4b = 5 \\ 3a+2b = 1 \end \right.> \Rightarrow <\left\< \begin 7a+4b = 5 \\ b = \frac<-3a+1> <2>= -1,5a+0,5 \end \right.> \Rightarrow <\left\< \begin 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end \right.> \Rightarrow <\left\< \begin a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end \right.> $

Пример 2. Найдите решение системы уравнений:

$а) <\left\< \begin \frac<4>-y = 7 | \times 4 \\ 3x+ \frac <2>= 9 | \times 2\end \right.> \Rightarrow <\left\< \begin x-4y = 28 \\ 6x+y = 18 \end \right.> \Rightarrow <\left\< \begin x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end \right.> \Rightarrow $

$\Rightarrow <\left\< \begin x = 4(y+7) \\ 24y+168+y = 18 \end \right.> \Rightarrow <\left\< \begin x = 4(y+7) \\ 25y = -150 \end \right.> \Rightarrow <\left\< \beginx = 4(-6+7) = 4 \\ y = -6 \end \right.>$

$ в) <\left\< \begin 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end \right.> \Rightarrow <\left\< \begin 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 10x-8y = -14 |:2 \\ x+8y = 25 \end \right.> \Rightarrow <\left\< \begin 5x-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin 5(-8y+25)-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin -40y+125-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin -44y = -132 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 3 \end \right.> $

$ г) <\left\< \begin 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end \right.> \Rightarrow <\left\< \begin 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end \right.> \Rightarrow <\left\< \begin 7x+22y = 57 \\ 2x-6y = 4 |:2 \end \right.>$

$$ \Rightarrow <\left\< \begin 7x+22y = 57 \\ x-3y = 2 \end \right.> \Rightarrow <\left\< \begin 7x+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin 7(3y+2)+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin 21y+14+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin 43y = 43 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin x = 5 \\ y = 1 \end \right.>$$

Пример 3*. Найдите решение системы уравнений:

Перепишем систему и найдём решение для новых переменных:

$$ <\left\< \begin 3a+8b = 5 \\ 12b-a = 2 \end \right.> \Rightarrow <\left\< \begin 3(12b-2)+8b = 5 \\ a = 12b-2 \end \right.> \Rightarrow <\left\< \begin 36b-6+8b = 5 \\ a = 12b-2 \end \right.> \Rightarrow $$

Источник

Системы уравнений

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.

Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют « x » и « y »), которые объединены в общую систему фигурной скобкой.

Например, система уравнений может быть задана следующим образом.

x + 5y = 7

3x − 2y = 4

Чтобы решить систему уравнений, нужно найти и « x », и « y ».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

x + 5y = 7

3x − 2y = 4

Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».

Чтобы выразить неизвестное, нужно выполнить два условия:

• перенести неизвестное, которое хотим выразить, в левую часть уравнения;
• разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.

Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.

При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.

x = 7 − 5y

3x − 2y = 4

Теперь, вместо « x » подставим во второе уравнение полученное выражение
« x = 7 − 5y » из первого уравнения.

x = 7 − 5y

3(7 − 5y) − 2y = 4

Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение « 3(7 − 5y) − 2y = 4 » отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*) .

x = 7 − 5y

3(7 − 5y) − 2y = 4 (*)

Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.

x = 7 − 5y

y = 1

x = 7 − 5 · 1

y = 1

x = 2

y = 1

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.

x + 5y = 7

3x − 2y = 4

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.

x + 5y = 7	(x + 5y) + (3x − 2y) = 7 + 4
+ =>	x + 5y + 3x − 2y = 11
3x − 2y = 4	4x + 3y = 11

При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

x + 5y = 7

3x − 2y = 4

Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».

Для этого умножим первое уравнение на « −3 ».

При умножении уравнения на число, на это число умножается каждый член уравнения.

x + 5y = 7 | ·(−3)

3x − 2y = 4

x · (−3) + 5y · (−3) = 7 · (−3)

3x − 2y = 4

−3x −15y = −21

3x − 2y = 4

Теперь сложим уравнения.

−3x −15y = −21	(−3x −15y ) + (3x − 2y) = −21 + 4
+ =>	− 3x − 15y + 3x − 2y = −21 + 4
3x − 2y = 4	−17y = −17 |:(−17)
y = 1

Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».

x = 7 − 5y

y = 1

x = 7 − 5 · 1

y = 1

x = 2

y = 1

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения « x ».

x = 17 + 3y

x − 2y = −13

Подставим вместо « x » во второе уравнение полученное выражение.

x = 17 + 3y

(17 + 3y) − 2y = −13 (*)

Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».

x = 17 + 3y

y = −30

x = 17 + 3 · (−30)

y = −30

x = 17 −90

y = −30

x = −73

y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

3(x − y) + 5x = 2(3x − 2)

4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

3x − 3y + 5x = 6x − 4

4x − 2x − 2y = 4 − 3y

8x − 3y = 6x − 4

2x −2y = 4 − 3y

8x − 3y − 6x = −4

2x −2y + 3y = 4

2x − 3y = −4

2x + y = 4

Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».

Для этого достаточно умножить первое уравнение на « −1 ».

2x − 3y = −4 | ·(−1)

2x + y = 4

2x · (−1) − 3y · (−1) = −4 · (−1)

2x + y = 4

−2x + 3y = 4

2x + y = 4

Теперь при сложении уравнений у нас останется только « y » в уравнении.

−2x + 3y = 4	(−2x + 3y ) + (2x + y) = 4 + 4
+ =>	− 2x + 3y + 2x + y = 4 + 4
2x + y = 4	4y = 8 | :4
y = 2

Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».

Источник