- Как считать на счетах
- Описание
- Сложение
- Вычитание
- Умножение
- Деление
- Приемы быстрого счета без калькулятора
- Устный счет — приемы
- 1. Умножение на 11
- 2. Быстрое возведение в квадрат
- 3. Умножение на 5
- 4. Умножение на 9
- 5. Умножение на 4
- 6. Подсчет чаевых
- 7. Сложное умножение
- 8. Деление на 5
- 9. Вычитание из 1000
- Интересные результаты:
- Любимая цифра.
- Угадать возраст.
- Всегда девятка
- Ручной счет или машинный?
- 9 необычных способов научить ребенка считать
- Метод «Камера хранения»
- Метод «Руки»
- Метод «Кузнечик»
- Метод «Рожки»
- Метод «Склад»
- «Итальянский метод умножения»
- «Японский метод умножения»
- Метод «Площадь»
- Метод «Массив»
Как считать на счетах

В данной статье вы прочитаете, как научиться правильно считать на русских счетах. Вероятно, многие молодые люди ни разу не видели живьем такой арифметический инструмент, как счеты. А кто и видел, скорее всего, не знает, что с помощью этого инструмента можно научиться быстро складывать, вычитать и даже умножать и делить достаточно большие числа. Конечно, сегодня это не так актуально. Но в рамках раздела, посвященного устному счету, думаю, многим будет интересно прочитать о таком популярном приспособлении, облегчающем устный счет, но не исключающим его полностью.
Описание
Знаменитые деревянные счеты, изображенные на рисунке ниже, повсеместно использовались в СССР первые две трети двадцатого века в основном для операций сложения и вычитания. Как же кассиры и бухгалтера пользовались этими русскими счетами? Давайте разберемся. Если же вы умеете пользоваться счетами, то можете перейти сразу к описанию более сложных операций.
В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть четвертаки (например, 25 копеек). Черным цветом выделены центральные костяшки (для удобства).
Набор числа. Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.
Но набор числа, это только начало. По-настоящему пользоваться деревянными счетами, значит совершать арифметические операции.
Сложение
Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов (именно с нижних!). Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, смотрите пример ниже (987 + 134 = 1 121):
Вычитание
Вычитание на счетах производится точно таким же образом, как сложение, – сверху вниз. Только если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число нехвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже смотрите пример, как правильно считать разность на русских счетах (121 – 98 = 23):
Умножение
Умножение на счетах является не самым быстрым и простым. В некоторых случаях, гораздо проще воспользоваться навыками быстрого умножения в уме. Однако в рамках данной статьи приведены некоторые методики умножения на деревянных счетах. Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой (при умножении на 2), и повторить эту процедуру при умножении на 3. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Что касается умножения на 5, как вы можете убедиться из этого урока, оно равносильно делению на 2 и последующему умножению на 10. В этом случае, после деления на 2 вы просто переносите разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.
Деление
Деление на русских счетах является достаточно сложной процедурой. Использовать для этого счеты иногда просто иррационально. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов и хорошего развития внимания и краткосрочной памяти.
Источник
Приемы быстрого счета без калькулятора
Хоть и считается, что математика наводит ужас на значительную часть населения, но деньги считать умеют все. И вот как раз влет это умеют делать люди, далекие от математики.
Помнится, бабушка моего мужа показывала ему на пальцах таблицу умножения на 9. Никакого образования, только огромная практика торговли редиской и клубникой на рынке!
Так вот сегодня я предлагаю вам несколько интересненьких приемов устного счета. Ведь сколько бы замечательных гаджетов (телефоны, смартфоны, айподы и айпады, ай, да чего там…) своя голова она всегда лучше.
Устный счет — приемы
Итак, читаем, тут же проверяем и запоминаем приемы вычисления в уме.
1. Умножение на 11
Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:
53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583
59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.
85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225
45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.
Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435
4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58×4 = (58×2) + (58×2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это.
Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
И, как следствие): чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину. Например,
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 все равно, что:
16×250 все равно, что:
8×500 все равно, что:
4×1000 = 4,000
8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352
И, напоследок, несколько математических трюков:
Интересные результаты:
1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321
1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 + 10 = 1111111111
9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888
1 х 8 + 1 = 9
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321
Любимая цифра.
Предложите задумать свою любимую цифру. А теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.
Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.
Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.
Угадать возраст.
Умножаем число своих лет на 10, затем любое однозначное число умножить на 9, из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.
Всегда девятка
Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.
Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.
Источник
Ручной счет или машинный?
04.01.2011, 20:27
Расчеты конструкций (SCAD 11.5; Мономах 4.5; STARK ES); Техническое Обследование Зданий и Сооружений
Proectant,
В принципе все так и должно быть, как пишешь:
1. Нагрузки
2. Внутренние усилия в элементах
3. Подбор сечений и армирования
Пункты 1 и 3 — делаются «врукопашную», но иногда врукопашную собираешь только нагрузки — да и то не всегда — например часть нагрузок — пульсация, сейсмика задается автоматически в программных комплексах, да и вручную не все можно посчитать — например определение частот и форм колебаний в сейсмике. (довольно таки муторно. )
| мои руководители говорят: «В ФОК загони и все, он тебе все выдаст». |
Это еще ничего, что у тебя руководители — конструкторы.
А вот надо мной например никого нет, решения принимаю я сам, чертит напарник — а считать мне приходится — несколько монолитных блоков в сейсмоопасном районе, сейсмичность площадки 9-10 баллов.
Вернее надо мной есть — тупо-дебильные манагеры-помы-замы-гипы-гапы, в общем клоуны. которые всю жизнь сидели на управленческих позициях и о проектировании и расчетах вообще понятия не имеют — для них главное — время и скорость проектирования (им бы еще деревянную лошадку на гнутых салазках купить+шашку и буденовку)
Применение программных комплексов происходит на мой взгляд по двум основным причинам:
1. Не все можно «посчитать ручками»
2. Катастрофическая нехватка времени, которое тупо определили для конструкторов манагеры или балбес-дерик, когда договор на проектирование объекта с заказчиком подписывал, уменьшая время (чтоб заказчик в другую фирму не ушел) на проектирование от фонаря.
к тому же иногда -когда уже расчетная схема в МКЭ-программе готова и заканчиваешь выпуск рабочки, приходит арх и говорит: «меня сегодня ночью муза посетила — в общем все переделываем — теперь у нас будет не 5 этажей а 25, здание будет не квадратное в плане а круглое с треугольными окошками». Тогда и происходят гонки с применением МКЭ-программ, когда еле успеваешь ручками собрать нагрузки, вогнать все в новую расчетную схему, а усилия из схемы вбубениваешь в Арбат, выдаешь чертежникам диаметры и выбираешь несколько секунд для контроля их рабочки — чтобы они верхнию и нижнию арматуры не попутали.
Такая вот дребедень.
Хотя конечно же отдельные элементы нужно в обязательном порядке просчитывать «врукопашную» — просто так все перед глазами, а заодно «рукопашные» расчеты отдельных элементов — это хороший контроль армирования получается.
Источник
9 необычных способов научить ребенка считать
Ваш ребенок сталкивается с проблемами решения математических задач?
Скорее всего это связано с непониманием ребенком сути выполняемых действий.
В последние годы сильно изменился подход к преподаванию математических понятий в школе.
Многие вещи, которые наглядно объяснялись раньше, сейчас даются детям в сложных и непонятных терминах, а учителя перекладывают объяснение материала на плечи родителей.
Именно поэтому многие дети испытывают проблемы со счетом и одна из важных задач родителей — помочь детям понять смысл математических действий.
В данной статье мы сделали подборку необычных методов и приемов для объяснения детям тем «сложение», «вычитание», «умножение», «состав числа», которые помогут вам и вашему ребенку по-новому взглянуть на непонятные темы.
Метод «Камера хранения»
Данный метод позволяет показать ребенку состав числа.
Представляет собой набор из 10 ячеек с точками внутри. Дети видят, как различные комбинации чисел составляют счет в пределах 10. Прием «камера хранения» особенно хорош в случае, когда надо показать, как работает вычитание.
Все дети в магазинах видели камеры хранения-ячейки. Нарисовав камеру хранения на бумаге, вы можете положить в нее что-то, или забрать. Ребенку остается посчитать, сколько ячеек свободны, а сколько заняты.
Метод «Руки»
Для этого метода необходимо использовать «руки» числа, для того, чтобы ребенок увидел соотношение между числами.
Человек держит какое-то количество предметов. При этом известно общее число и сколько в одной руке. Ребенок должен увидеть и сказать, сколько во второй.
На первом рисунке соотношение между цифрами 3 и 10 показано добавлением числа 7 в пустой круг (3 + 7 = 10). Это помогает детям понять, как один номер можно разбить на более мелкие части. Во второй руке — семь. На втором рисунке — во первой руке два.
Метод «Кузнечик»
Данный метод позволяет наглядно показать ребенку сложение и вычитание.
Рисуется прямая линия. Ребенок может использовать любое число и любое место на строке в качестве стартового места для запуска «кузнечика».
На рисунке цифра 37 — это начальное место. С этой точки отправляется кузнечик. Допустим, он пропрыгал 26 метров(нужно прибавить 26)
От начальной точки каждые 10 метров мы отмечаем большой дугой и пишем внизу новое число. Когда десятки закончились, маленькой дугой мы добавляем единицы и считаем какое число получилось.
Данный прием позволяет детям добавлять или вычитать визуально, и его можно использовать, чтобы помочь детям решить вычислительные проблемы.
Метод «Рожки»
Данный метод позволяет наглядно показать ребенку сложения многозначных чисел.
Рожки — это стратегия решения математических задач путем разбиения числа на цифры.
Например, 37 представляется в виде суммы чисел 30 и 7.
Как только вы «опускаете рожки» числа вниз, вы можете добавить или вычесть значения левых и правых «рогов», чтобы получить ответ.
 Метод «Склад»
Метод «Склад»
«Склад» — это стратегия для решения проблем сложения и вычитания чисел в пределах тысячи.
Для этого применяется таблица, разделенная на сотни, десятки и единицы.
При этом можно провести «перемещение».
Каждое число вписывается на ячейку «склада» в определенное место. Например, 43 будет означать 4 десятки и 3 единицы. Дальше можно наглядно показывать ребенку, что можно убрать один десяток и добавить десять единиц.
После того, как ребенок понял, что можно перемещать одно число в рамках собственных ячеек, можно добавлять второй склад, который нужно либо наполнить из текущего(вычитание), либо наоборот освободить и загрузить текущий склад(сложение)
Это помогает детям понять, когда «брать» и «переносить» цифры из одного места в другое.
«Итальянский метод умножения»
Это метод разбиения чисел на цифры, позволяющий решить проблему с умножением.
В таблице цифры делятся на значения и умножаются отдельно. После умножения каждого числа общие значения складываются вместе.
Этот метод может быть полезен для детей, у которых есть проблемы с традиционным умножением, особенно при умножении больших чисел.
Записываем по бокам таблицы числа 32 и 26 разделив их на десятки и единицы. Перемножаем значения и результат фиксируем в таблице, на пересечении умножаемых чисел.
Складываем все полученные числа.
«Японский метод умножения»
Данный метод позволяет ребенку визуализировать умножение и решать примеры в рамках таблицы умножения и за ее пределами.
Например нам нужно умножить 12 на 12.
Шаг 1 — Горизонтально рисуем линии первого числа. Для каждого числа рисуется свое количество линий. Десятки и единицы разделяются промежутками. Например, для числа 12 единица рисуется одной линией. Двойка – чуть ниже двумя параллельными линиями. Для числа 36, 3 рисуется тремя линиями, 6 шестью параллельными линиями ниже и т.д.
Шаг 2 По аналогии с шагом 1, вертикальными линиями рисуем второе число 12:
Единицу – одной линией
Двойку – чуть отступив вправо двумя линиями
Шаг 3 Ставим на пересечениях линий точки
Шаг 4 Подсчитываем количество точек в трех группах, разделив их на «Рыбу»: хвост, голову и тело
Левый верхний угол – 1 (сотни)
Правый верхний и левый нижний углы (Диагональ) – 4 (десятки)
Правый нижний угол – 4 (единицы)
Шаг 5 Записываем результат: 144. Если у единиц или десятков получилось двухзначное число, то первая цифра добавляется к следующему разряду.
Метод «Площадь»
Данная модель использует длину и ширину прямоугольника или квадрата, чтобы разбить умножение. Числа разбиваются на прямоугольники.
Каждая форма вычисляется отдельно и ответы складываются вместе. Это еще один способ сделать математику более визуальной и наглядной для детей.
Метод «Массив»
Подобно методу «Площадь», массив представляет собой расположение объектов, которые представляют собой число.
Эта модель часто используется, чтобы помочь детям увидеть различные качества сложения и умножения, а так же понять смысл действия умножение.
Необычная подача материала позволяет сделать сложные вещи простыми, а непонятное — понятным.
Иногда ребенку достаточно просто один раз объяснить, как что-то работает и у него пропадают проблемы с определенной темой.
К большому сожалению, современная система образования не ставит целью сделать непонятное понятным, а сложное простым.
Наоборот, объяснения становятся все запутаннее и сложнее и детям с каждым годом все труднее учиться.
В школе спецагентов, в которой мы работаем вместе с детьми, мы учим детей простому решению сложных задач.
Благодаря месячной программе «молодого бойца» дети становятся спецагентами эффективного обучения и учатся решать сложные задачи легко и нестандартно.
За время курса дети осваивают «спецагентские приемы» пересказывать и запоминать длинные тексты, писать изложения и сочинения, запоминать числа, даты, формулы, стихи и иностранные слова.
Программу проходят как участники начальной школы, так и выпускники старших классов.
Благодаря индивидуальному подходу, специальному подбору упражнений, энергии, комадне и мотивации — каждый ребенок открывается и раскрывает суперспособности к обучению.
За программу мы передаем все инструменты эффективного обучения ребенку и Вы получаете ребенка, который любит учиться сам.
Старт третьего потока школы спецагентов уже 16 декабря и у нас осталось всего 5 мест в младшей группе.
Присоединяйтесь к нам прямо сейчас, пока есть места в этом году. Дайте ребенку спецтехники обучения и помогите ему сделать процесс обучения в школе легким и успешным
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Источник


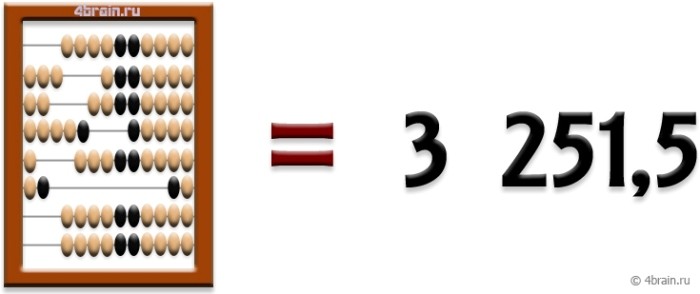

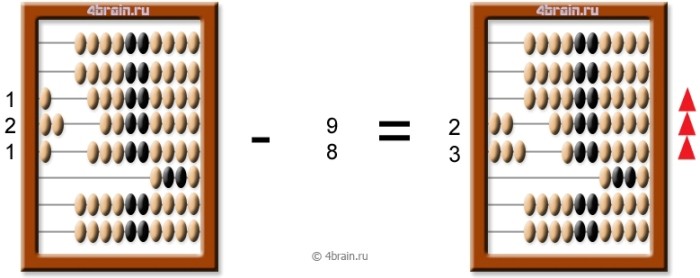










 Метод «Склад»
Метод «Склад»







