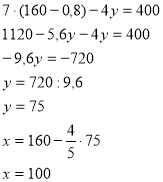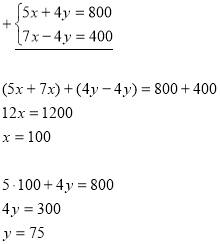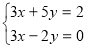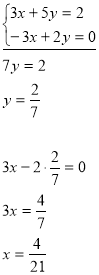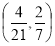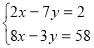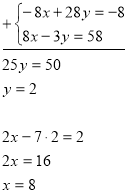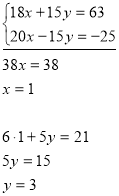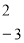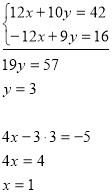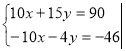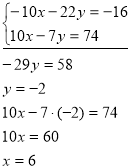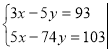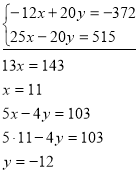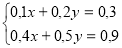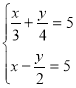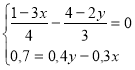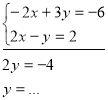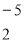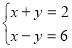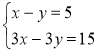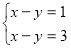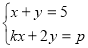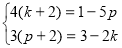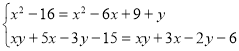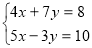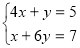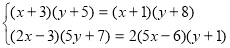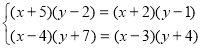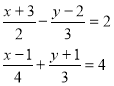Спосіб додавання
Привіт! На цьому уроці розглянемо ще один спосіб (і, нарешті, останній) розв’язування систем рівнянь — спосіб додавання. Для багатьох учнів він став улюбленим способом. Поїхали!
Трошки теорії (для тих, кому цікаво)
Даний метод заснований на використанні властивостей рівнянь, що відомі нам із попередніх класів, та використанні одного твердження, що стосується систем рівнянь. А саме:
Якщо одне з рівнянь системи замінити на рівняння, отримане шляхом додавання лівих і правих частин рівнянь системи, то отримана система буде мати такі ж розв’язки, що й початкова.
Переконаємося у правильності цього твердження на прикладі:
Розглянемо систему рівнянь: \[\begin
Додамо ліві і праві частини рівнянь системи: \[2x+y+4x-3y=6+2.\] \[6x-2y=8.\]
Замінимо друге рівняння системи на рівняння, яке отримали: \[\begin
Знайдемо розв’язок цієї системи способом підстановки:
З першого рівняння виразимо \(y=6-2x\) та підставимо до другого рівняння: \[6x-2(6-2x)=8.\] Розв’язуємо відносно \(x\). \[6x-12+4x=8,\] \[10x=20,\] \[x=2.\]
Знаходимо значення \(y\): \(y=6-2\cdot 2=2\). Отримали розв’язок системи \(\left(2;\;2\right)\), такий самий, як і першої системи.
Розглянутий приклад демонструє справедливість наведеного твердження. А як же спосіб додавання? Давайте перейдемо до його розгляду.
У чому полягає цей спосіб
Для того, щоб розв’язати систему рівнянь способом додавання, можна скористатися наступним алгоритмом:
Алгоритм розв’язування систем рівнянь способом додавання
- Перетворити одне (або обидва) рівняння системи таким чином, щоб коефіцієнти при одній із змінних були протилежними числами;
- Почленно додати ліві та праві частини рівнянь отриманої системи;
- Розв’язати отримане рівняння з однією змінною;
- Підставити отримане значення змінної до будь-якого рівняння системи;
- Знайти значення другої змінної;
- Записати відповідь.
Подивимось, як використати даний алгоритм до розв’язання системи із Прикладу 1:
Розв’язати систему рівнянь способом додавання: \[\color<#4682B4> <\begin
У результаті отримали систему \[\color<#4682B4> <\begin
Крок 3. З отриманого рівняння \(\color<#4682B4><10x=20>\) знаходимо значення \(\color<#4682B4>
Крок 4. Підставимо отримане значення змінної \(\color<#4682B4>
Крок 5. Розв’яжемо отримане рівняння, щоб знайти значення змінної \(y\): \[\color<#4682B4><8-3y=2,>\] \[\color<#4682B4><-3y=-6,>\] \[\color<#4682B4>
Крок 6. Ми знайшли значення змінних \(x\) та \(y\), і можемо записати відповідь.
Источник
Тема 6. Розв’язування систем лінійних рівнянь з двома невідомими способом додавання.
Розробка циклу уроків однієї з навчальних тем курсу алгебри „Системи лінійних рівнянь з двома змінними» для 7 класу. Шостий урок із даної теми
Тема 6.
Розв’язування систем лінійних рівнянь з двома невідомими способом додавання.
Мета: навчити учнів розв’язувати системи лінйних рівнянь з двома невідомими способом додавання; формувати культуру записів; забезпечити мотивацію навчання; сприяти засвоєнню учнями способів, засобів, які приводять до розуміння способу додавання; створити змістові та організаційні умови застосування учнями вивченого матеріалу; встановити правильність усвідомлення вивченого матеріалу; провести корекцію виявлених прогалин в усвідомленні учнями вивченого матеріалу.
Тип уроку: засвоєння нових знань.
- Організаційний момент. Перевірка домашнього завдання. Коригування опорних знань, умінь і навичок.
- Підготовка учнів до сприйняття нового матеріалу. Мотивація навчальної діяльності. Оголошення нового матеріалу.
- Вивчення нового матеріалу.
- Осмислення новихзнань, формування умінь та новичок при розв’язуванні задач і вправ.
- Закріплення, систематизація та узагальнення навчального матеріалу.
- Контрольно-коригуючий етап.
- Підбиття підсумків уроку. Інструктаж щодо виконання домашньої роботи.
І. Привітання, перевірка присутніх. Обговорення результатів. Корекція допущених помилок.
ІІ. Розв’язування задачі на складання системи лінійних рівнянь з двома невідомими. Формування в учнів розуміння вибору раціональнішого способу.
У багатьох системах рівнянь графічний спосіб, як і спосіб підстановки, незручні, а іноді й ускладнюють розв’язування деяких систем рівнянь.
Розглянемо для прикладу задачу, яка розв’язується за допомо гою системи рівнянь.
Задача 1 . Маса 5 великих і 4 малих шоколадок становить 800 г. 7 великих шоколадок мають масу на 400 г більшу, ніж 4 малих. Яка маса одної великої та одної малої шоколадок?
х — маса великої шоколадки;
у — маса малої шоколадки;
5х — маса п’яти великих шоколадок;
4у — маса всіх малих шоколадок;
7х — маса семи великих шоколадок;
5х + 4х — маса малих і великих шоколадок, узятих разом;
7х — 4у — різниця між масою семи великих і чотирьох малих шоколадок.
З умови задачі випливає система таких двох рівнянь:
Пропонуємо два способи розв’язання одержаної системи рів нянь.
Спосіб підстановки:
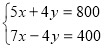
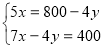
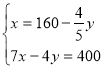
Спосіб додавання:
Отже, розв’язком даної системи є пара чисел: (100; 75).
Відповідь: 100 г, 75 г.
Поясніть кожне з цих розв’язань. Який зі способів простіший і зрозуміліший? Згідно з якою властивістю рівнянь записаний тре тій рядок у правому стовпчику? А як би ви розв’язали цю систему рівнянь?
Задача 2. Як розв’язати таку систему рівнянь:
Яку властивість рівнянь треба використати, щоб коефіцієнти при одній зі змінних були протилежними числами?
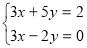
Відповідь:
Задача 3. Виникає ще одне запитання. Як бути, якщо коефіцієнти при одних і тих же змінних не є протилежними числами?
Наприклад,
Оскільки коефіцієнт при змінній х у другому рівнянні в 4 рази більший, ніж у першому, то обидві частини першого рівняння помножимо на -4. У результаті дістанемо рівносильну систему рівнянь:
Задача 4. І все ж, як розвязхати систему рівнянь способом додавання, якщо коефіцієнти як при змінній х, так і при змінній у, не є кратними числами?
Розглянемо два випадки розв’язання систем рівнянь способом додавання.
Перший випадок:
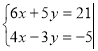
Другий випадок:
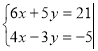
ІІІ. Підведення учнів до вивчення нового матеріалу.
У чому полягає суть розв’язання системи рівнянь способом додавання на основі розв’язаних систем зробимо висновок.
Способом додавання можна розв’язати таку систему рівнянь, у якій коефіцієнти при одній і тій же змінній в обох рівняннях є протилежними числами.
Наприклад, 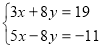
Якщо ж запропонована система не має такого вигляду, то неважко звести будь-яку систему лінйних рівнянь з двома змінними до такої системи рівнянь, в якій коефіцієнти при одній і тій же будь-якій змінній є протилежними числами.
Наприклад, 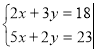
Ми розглянули приклади розв’язування систем спо собом додавання. Розв’язуючи системи двох лінійних рів нянь з двома змінними способом додавання, роблять так:
- множать почленно рівняння системи, підбираючи множники так, щоб коефіцієнти при одній із змінних стали протилежними числами;
- додають почленно ліві і праві частини рівнянь системи;
- розв’язують утворене рівняння з однією змінною;
- знаходять відповідне значення другої змінної.
Зауважимо, що коли коефіцієнти при одній зі змінних є протилежними числами, то розв’язування відразу починають з по членного додавання рівнянь.
Мабуть, вам зрозуміло, що систему рівнянь доцільно розв’язувати одним із двох способів: підстановки або додавання.
Який зі способів кращий? — Це залежить від коефіцієнтів, що є при змінних х та у.
1. Робота із електронним підручником.
2. Розбір розв’язаних систем по електронному підручнику.
V . Розв’язування систем способом підстановки.
№1

У рівняннях цієї системи коефіцієнти при у — проти лежні числа. Додавши почленно ліві і праві частини рів нянь, дістанемо рівняння з однією змінною:
Зх = 33.
Замінимо одне з рівнянь системи (1) наприклад перше, ріпиянням 8х = 33. Дістанемо систему:

Система (2) рівносильна системі (1).
Розвяжемо систему (2). З рівняння 3х=33 знаходимо, що х=11. підставивши це значення х у рівняння х – 3у =38, дістанемо рівняння зі змінною у:
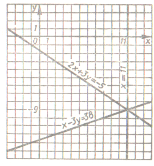
Скориставшись тим, що в рівняннях системи (1) кое фіцієнти при у є протилежними числами, ми звели її розв’язування до розв’язування рівносильної системи (2) в якій одне з рівнянь ма є тільки одну змінну.
Геометричне рівносильність систем (1) і (2) означа є , що графіки рівнянь 2х + Зу = — 5 та х — Зу = 38 пере тинаються у тій самій точці, що і графіки рівнянь Зх =33 і х — Зу = 38, тобто всі три прямі перетинаються в одній точці .
№2
Розв ’ яжемо систему:
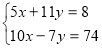
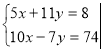
№3
Підберемо множники до рівнянь системи так, щоб після множення на них коефіцієнти при у стали проти лежними числами. Помножимо перше рівняння систем и на — 4, а друге на 5, дістанемо:
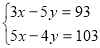
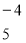
Відповідь: (11; -12)
№4
№5
№6
№7
№8
Закінчіть розв’язування системи рівнянь способом додавання:
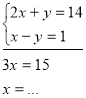
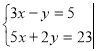
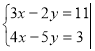
№9
За допомогою алгебраїчного і графічного розв’язань покажіть, що подані нижче системи рівнянь мають тільки один розв’язок:
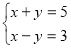
№10
За допомогою алгебраїчного і графічного розв’язань покажіть, що подані нижче системи рівнянь мають безліч розв’язків:
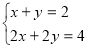
№11
За допомогою алгебраїчного і графічного розв’язань покажіть, що подані нижче системи рівнянь не мають розв’язків:
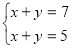
№12
Маємо системи рівнянь:
Підберіть такі значення для k та p , щоб система рівнянь:
- мала один розв ’ язок
- мала безліч розв’язків
- не мала розв’язків.
№13
Розв’яж іть систем и рівнянь стосовно букв, які входять у рівняння системи :
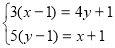
№14
Чи існує таке значення змінних х і у, щоб сума виразів 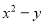
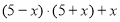
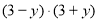
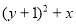
№15
Чи рівносильні системи рівнянь:
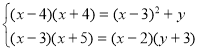
VI . Написання самостійної роботи(по рівнях)
VII . Підсумок уроку. Повідомлення домашнього завдання.
- Вивчити теоретичний матеріал.
- Розв’язати письмово завдання.
Источник