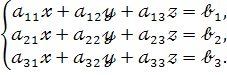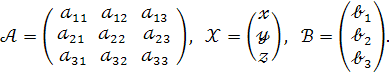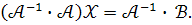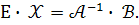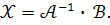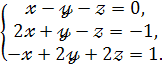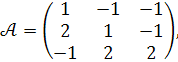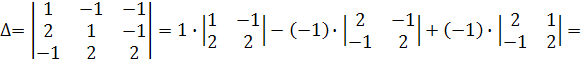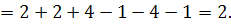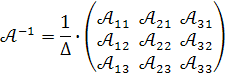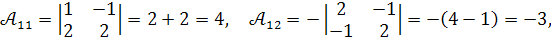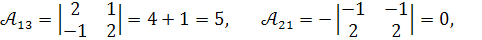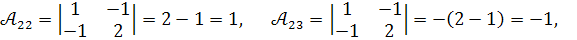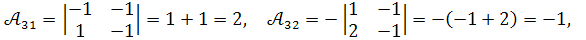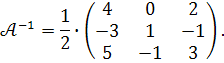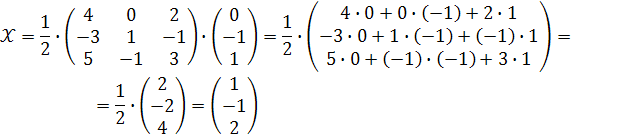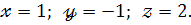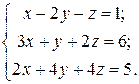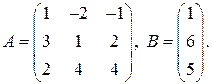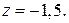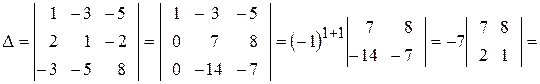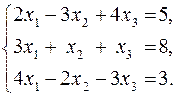- Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Матричний метод. Метод оберненої матриці
- Розв’язати систему лінійних рівнянь матричним методом
- Ввід даних в калькулятор для розв’язання системи лінійних рівнянь матричним методом
- Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь матричним методом
- Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Метод Гауса
- Розв’язати систему лінійних рівнянь методом Гауса
- Ввід даних в калькулятор для розв’язання системи лінійних рівнянь методом Гауса
- Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь методом Гауса
- Розв’язування систем лінійних рівнянь матричним способом.
- Матричний спосіб розв’язання систем
- Розв’язання типового варіанта. В задачах варіантів 1-25 розв’язати задану систему лінійних алгебраїчних рівнянь трьома методами: 1) за формулами Крамера; 2) матричним методом; 3) методом
Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Матричний метод. Метод оберненої матриці
Скориставшись цим онлайн калькулятором для розв’язання системи лінійних рівнянь (СЛР) матричним методом (методом оберненої матриці), ви зможете дуже просто і швидко знайти розв’язок системи рівнянь.
Скориставшись онлайн калькулятором для розв’язання системи лінійних рівнянь матричним методом (методом оберненої матриці) ви отримаєте детальний розв’язок вашого прикладу, який дозволить зрозуміти алгоритм розв’язання таких задач і закріпити вивчений матеріал.
Розв’язати систему лінійних рівнянь матричним методом
Змінити назви змінних в системі
Заповніть систему лінійних рівнянь:
Ввід даних в калькулятор для розв’язання системи лінійних рівнянь матричним методом
- В онлайн калькулятор можна вводити числа або дроби. Більш детально читайте в правилах вводу чисел.
- Для зміни в рівнянні знаків з «+» на «-» введіть від’ємне число.
- Якщо у вашому рівнянні відсутня яка-небудь змінна, то у відповідне поле в калькуляторі введіть нуль.
- Якщо в рівнянні попереду змінною відсутні числа, то в відповідне поле калькулятора введіть одиницю.
Наприклад, лінійне рівняння x 1 — 7 x 2 — x 4 = 2
буде вводитися в калькулятор наступним чином:
Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь матричним методом
- Використовуйте кнопки , , та на клавіатурі, для переміщення між полями калькулятору.
- Замість x 1, x 2, . ви можете ввести власні назви змінних.
Вводити можна лише числа або дроби (-2.4, 5/7, . ). Більш детально читайте в правилах вводу чисел.
Источник
Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Метод Гауса
Скориставшись цим онлайн калькулятором для розв’язання системи лінійних рівнянь (СЛР) методом Гауса, ви зможете дуже просто і швидко знайти розв’язок системи рівнянь.
Скориставшись онлайн калькулятором для розв’язання системи лінійних рівнянь методом Гауса ви отримаєте детальний розв’язок вашого прикладу, який дозволить зрозуміти алгоритм розв’язання таких задач і закріпити вивчений матеріал.
Розв’язати систему лінійних рівнянь методом Гауса
Змінити назви змінних в системі
Заповніть систему лінійних рівнянь:
Ввід даних в калькулятор для розв’язання системи лінійних рівнянь методом Гауса
- В онлайн калькулятор можна вводити числа або дроби. Більш детально читайте в правилах вводу чисел.
- Для зміни в рівнянні знаків з «+» на «-» введіть від’ємне число.
- Якщо у вашому рівнянні відсутня яка-небудь змінна, то у відповідне поле в калькуляторі введіть нуль.
- Якщо в рівнянні попереду змінною відсутні числа, то в відповідне поле калькулятора введіть одиницю.
Наприклад, лінійне рівняння x 1 — 7 x 2 — x 4 = 2
буде вводитися в калькулятор наступним чином:
Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь методом Гауса
- Використовуйте кнопки , , та на клавіатурі, для переміщення між полями калькулятору.
- Замість x 1, x 2, . ви можете ввести власні назви змінних.
Вводити можна лише числа або дроби (-2.4, 5/7, . ). Більш детально читайте в правилах вводу чисел.
Источник
Розв’язування систем лінійних рівнянь матричним способом.
Розглянемо систему трьох лінійних рівнянь відносно трьох невідомих
Її можна записати у матричному вигляді. Для цього позначимо
Систему можна записати так :
Матричним способом можна розв’язати систему тільки тоді, коли
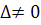
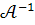
Помножимо систему на 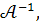
Враховауючи властивість добутку, маємо :
За визначенням оберененої матриці, маємо
Оскільки 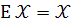
Це розв’язок систем у матричній формі.
Приклад 10. Розв’язати систему рівнянь матричним способом :
Запишемо систему у матричній формі
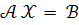
Перевіримо, чи
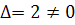
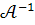
Обчислимо алгебраїчні доповнення :
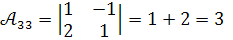
Отже
Відповідь :
Питання для самоконтролю.
1. Як обчислюється визначник другого порядку ?
2. Що таке мінор та алгебраїчне доповнення?
3. Як обчислюється визначник третього порядку?
4. Які властивості визначників?
5. Які дії виконуються над матрицями?
6. За якою формулою знаходиться обернена матриця?
7. Як розв’язується система лінійних рівнянь методом Гауса?
8. Як розв’язується система лінійних рівнянь за формулами Крамера?
9. Як розв’язується система лінійних рівнянь матричним способом?
Источник
Матричний спосіб розв’язання систем
Система п лінійних алгебраїчних рівнянь з п невідомими.
Нехай задано систему 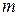
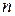
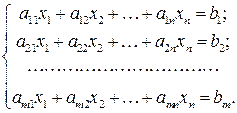
Означення. Система (1.9) називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має розв’язків.
Сумісність системи означає, що існує принаймні один набір чисел 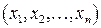
Запишемо коефіцієнти при невідомих з кожного рівняння системи у відповідний рядок матриці:
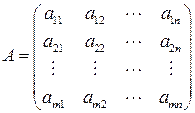
Цю матрицю називають основною матрицею системи (1.9). Розглянемо матричний запис і матричний спосіб розв’язання системи лінійних алгебраїчних рівнянь.
Нехай задано систему 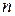
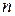
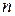
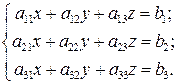
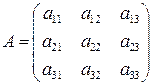
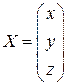
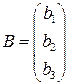
Тоді, використовуючи правило множення матриць (1.7), систему (1.11) можна записати в еквівалентній матричній формі:
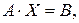
де А –матриця системи, В – задана матриця -стовпець, Х – невідома матриця -стовпець. Розв’язком рівняння (1.13) є такий вектор-стовпець Х, який обертає рівняння (1.13) у вірну рівність.
Якщо 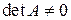
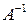
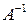
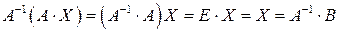
Отже розв’язок рівняння (1.13) дається формулою
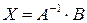
Ця формула особливо зручна, коли потрібно розв’язувати системи з однією і тією ж матрицею А і різними стовпцями правих частин B.
Таким чином, якщо матриця квадратної СЛАР невироджена, система має єдиний розв’язок.
Приклад. Розв’язати систему
Матрицю, обернену до матриці А, було обчислено в попередньому пункті:
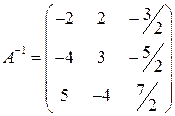
Тоді за формулою (1.14)
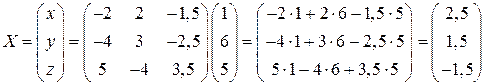
Відповідь: х=2,5; у=1,5;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Розв’язання типового варіанта. В задачах варіантів 1-25 розв’язати задану систему лінійних алгебраїчних рівнянь трьома методами: 1) за формулами Крамера; 2) матричним методом; 3) методом
Завдання 2.
В задачах варіантів 1-25 розв’язати задану систему лінійних алгебраїчних рівнянь трьома методами: 1) за формулами Крамера; 2) матричним методом; 3) методом Жордана-Гаусса.
1.  3. 3. 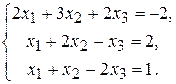 5. 5. 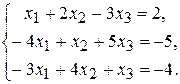 7. 7. 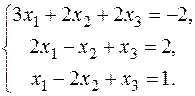 9. 9. 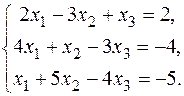 11. 11. 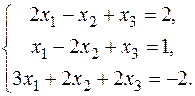 | 2. 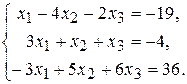 4. 4. 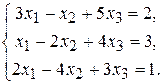 6. 6. 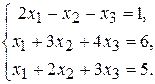 8. 8. 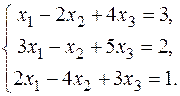 10. 10. 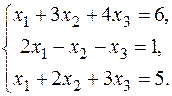 12. 12. 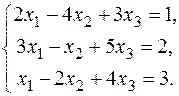  |
13. 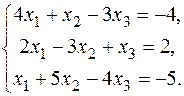 15. 15. 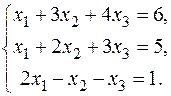 17. 17. 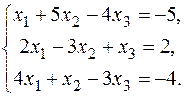 19. 19. 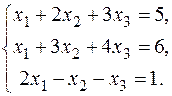 21. 21. 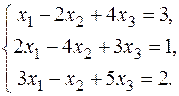 23. 23. 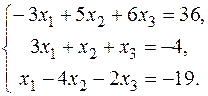 25. 25.  | 14. 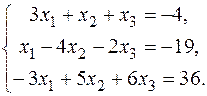 16. 16. 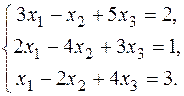 18. 18. 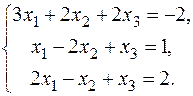 20. 20. 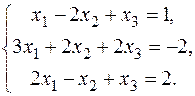 22. 22. 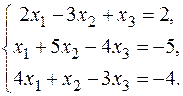 24. 24. 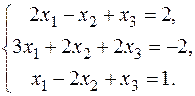 |
1. Обчислити визначник четвертого порядку
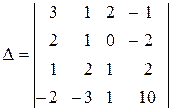
► Використаємо метод зниження порядку, який основано на застосуванні правила обчислення визначників за допомогою розкладання за елементами деякого рядка (стовпця). Використовуючи при цьому властивість визначників про лінійну комбінацію елементів рядків (стовпців), обертаємо в нулі усі, крім одного, елементи деякого рядка (стовпця).
В нашому випадку помножимо послідовно третій рядок на 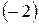
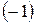
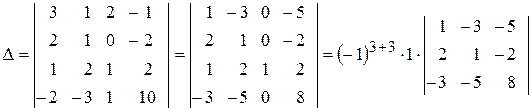
Далі обертаємо в нулі елементи першого стовпця, окрім елементу 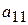
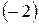
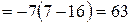
2. Розв’язати систему лінійних рівнянь двома способами: за правилом Крамера та за допомогою матриці, оберненої до матриці системи
► 1) Формули Крамера мають вигляд:
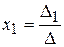
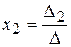
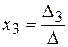
де 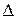
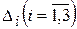
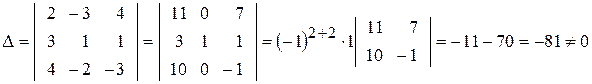
Отже, система має єдиний розв’язок.
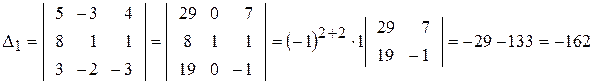
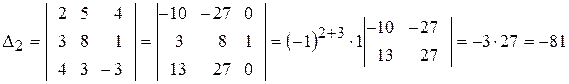
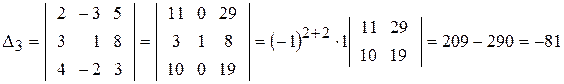
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник