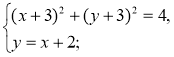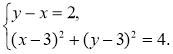- Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Метод Гауса
- Розв’язати систему лінійних рівнянь методом Гауса
- Ввід даних в калькулятор для розв’язання системи лінійних рівнянь методом Гауса
- Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь методом Гауса
- Математика. Повний повторювальний курс. Підготовка до ЗНО та ДПА
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними.
- Тема 2. Системи лінійних рівнянь з двома змінними. Графічний спосіб розв’язування таких систем.
Онлайн калькулятор. Розв’язання систем рівнянь (СЛР). Метод Гауса
Скориставшись цим онлайн калькулятором для розв’язання системи лінійних рівнянь (СЛР) методом Гауса, ви зможете дуже просто і швидко знайти розв’язок системи рівнянь.
Скориставшись онлайн калькулятором для розв’язання системи лінійних рівнянь методом Гауса ви отримаєте детальний розв’язок вашого прикладу, який дозволить зрозуміти алгоритм розв’язання таких задач і закріпити вивчений матеріал.
Розв’язати систему лінійних рівнянь методом Гауса
Змінити назви змінних в системі
Заповніть систему лінійних рівнянь:
Ввід даних в калькулятор для розв’язання системи лінійних рівнянь методом Гауса
- В онлайн калькулятор можна вводити числа або дроби. Більш детально читайте в правилах вводу чисел.
- Для зміни в рівнянні знаків з «+» на «-» введіть від’ємне число.
- Якщо у вашому рівнянні відсутня яка-небудь змінна, то у відповідне поле в калькуляторі введіть нуль.
- Якщо в рівнянні попереду змінною відсутні числа, то в відповідне поле калькулятора введіть одиницю.
Наприклад, лінійне рівняння x 1 — 7 x 2 — x 4 = 2
буде вводитися в калькулятор наступним чином:
Додаткові можливості калькулятору для розв’язання системи лінійних рівнянь методом Гауса
- Використовуйте кнопки , , та на клавіатурі, для переміщення між полями калькулятору.
- Замість x 1, x 2, . ви можете ввести власні назви змінних.
Вводити можна лише числа або дроби (-2.4, 5/7, . ). Більш детально читайте в правилах вводу чисел.
Источник
Математика. Повний повторювальний курс. Підготовка до ЗНО та ДПА
АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ
Розділ II. РІВНЯННЯ І НЕРІВНОСТІ
§4. МЕТОДИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ.
3. Графічний спосіб розв’язування систем.
Розв’язуючи систему лінійних рівнянь з двома змінними графічним способом, необхідно:
1) побудувати графіки рівнянь на одній координатній площині;
2) знайти координати точки перетину графіків або впевнитися в тому, що графіки рівнянь не перетинаються (є паралельними) або збігаються;
3) якщо координати точки перетину — цілі числа, то виконати перевірку; якщо ні, то розв’язок системи визначити наближено;
4) дати відповідь.
Приклад. Розв’яжіть графічним способом систему рівнянь
Графіки рівнянь зображено на малюнку 25. Графіки перетинаються у точці М(3;-2).
Перевірка: 3 — (-2) = 5, 2 ∙ 3 + (-2) = 4. Отже, пара чисел (3; -2) є розв’язком заданої системи:
Використовуючи сайт ви погоджуєтесь з правилами користування
Віртуальна читальня освітніх матеріалів для студентів, вчителів, учнів та батьків.
Наш сайт не претендує на авторство розміщених матеріалів. Ми тільки конвертуємо у зручний формат матеріали з мережі Інтернет які знаходяться у відкритому доступі та надіслані нашими відвідувачами.
Якщо ви являєтесь володарем авторського права на будь-який розміщений у нас матеріал і маєте намір видалити його зверніться для узгодження до адміністратора сайту.
Ми приєднуємось до закону про авторське право в цифрову епоху DMCA прийнятим за основу взаємовідносин в площині вирішення питань авторських прав в мережі Інтернет. Тому підтримуємо загальновживаний механізм «повідомлення-видалення» для об’єктів авторського права і завжди йдемо на зустріч правовласникам.
Копіюючи матеріали во повинні узгодити можливість їх використання з авторами. Наш сайт не несе відподвідальність за копіювання матеріалів нашими користувачами.
© 2008-2021 Всі права на дизайн сайту належать С.Є.А.
Источник
Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними.
Тема уроку. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними.
Мета уроку: домогтися засвоєння учнями змісту: поняття «що означає розв’язати систему рівнянь з двома змінними»; поняття розв’язку системи рівнянь з двома змінними; схеми дій (алгоритму) для відшукання розв’язку системи рівнянь з двома змінними графічним способом. Виробити вміння: відтворювати зміст вивчених понять та алгоритму; за стосовувати їх для розв’язування вправ на побудову гра фіків рівнянь з двома змінними та графічне розв’язування систем рівнянь з двома змінними.
Тип уроку: формування знань, вироблення вмінь.
Наочність та обладнання: опорний конспект № 19.
Хід уроку
І. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II . Перевірка домашнього завдання
Учитель організує роботу учнів з перевірки виконання вправ домашнього завдання за зразком (особливу увагу звертаємо на вправи на повторення: коментуючи дії, що були зроблені учня ми при їх виконанні, проводимо не тільки актуалізацію опорних знань, але й ще створюємо мотивацію для навчальної діяльності учнів).
III . Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Після проведеної перевірки виконання вправ домашнього за вдання вчитель спрямовує думку учнів на роздуми з приводу того, що у 7 класі, розглянувши питання про зміст поняття «лінійне рівняння з двома змінними», учні дослідили питання не тільки про побудову графіка лінійного рівняння з двома змінними, але й роз глянули поняття системи лінійних рівнянь 3 двома змінними та вивчили способи розв’язування таких систем. Після цих міркувань цілком логічним буде сформулювати питання! а чи можна, вивчив ши питання про існування нелінійних рівнянь з двома змінними, розглянута питання про існування та розв’язування систем таких рівнянь? Якщо це можливо, то на даному уроці слід розглянути питання про системи нелінійних рівнянь та спосіб розв’язування таких систем за допомогою графіків рівнянь з двома змінними. Останнє твердження виражає основну дидактичну мету даного і наступного уроків.
IV . Актуалізація опорних знань та вмінь учнів
Усні вправи
- Чи є пара чисел (2; 0) розв’язком рівняння:
4) ( x 2 – 1) 2 + ( y + 2) 2 = 0; 5) 4 х 2 – 12 ху + 9 у 2 = -1.
- Виразіть одну змінну через іншу з рівняння:
- Побудуйте схематично (опишіть вигляд) графік функції:
1) у = 5 х; 2) у = 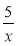
V . Формування знань
План вивчення нового матеріалу
- Поняття системи рівнянь з двома змінними та її розв’язку. Що означає «розв’язати систему рівнянь з двома змінними».
- Як розв’язати систему рівнянь з двома змінними графічним способом.
Опорний конспект № 19
Системи рівнянь з двома змінними
Якщо ставиться завдання знайти всі спільні розв’язки двох (і більше) рівнянь з двома змінними, то кажуть, що треба розв’язати систему рівнянь з двома змінними.
Розв’язком системи рівнянь з двома змінними х і у на зивається така пара значень змінних (х; у), яка є розв’язком кожного з рівнянь системи.
Наприклад, пара (2; 3) є розв’язком системи рівнянь 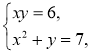
Розв’язати систему рівнянь з двома змінними означає зна йти всі її розв’язки, або довести, що їх немає. ! Якщо система не має розв’язків, її називають несумісною.
Як розв’язати систему рівнянь з двома змінними х і у
графічним способом
1. Будуємо графіки кожного з рівнянь системи в тій самій прямокутній системі координат.
2. Знаходимо всі точки перетину побудованих графіків і визна чаємо їхні координати. Ці координати є розв’язками даної системи рівнянь.
Розв’язування систем рівнянь за допомогою побудови графіків рівнянь з двома змінними дозволяє наочно обґрунтувати кількість розв’язків системи рівнянь. Матеріал цього та наступного уроків дає можливість повторити широке коло питань курсу алгебри дев’ятирічної школи та деякі питання курсу геометрії. Успішно му протіканню цієї роботи сприятиме підготовча робота з повто рення основних понять попереднього уроку та питань, розгляну тих у 7 класі під час вивчення систем лінійних рівнянь з двома змінними, проведена на етапі актуалізації опорних знань та вмінь учнів.
VI . Формування вмінь
Усні вправи
- Чи є розв’язком системи рівнянь
пара чисел:
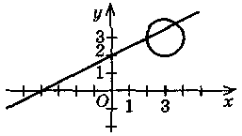
- Відомо, що система рівнянь
має три розв’язки. Скільки точок перетину мають графіки цих рівнянь?
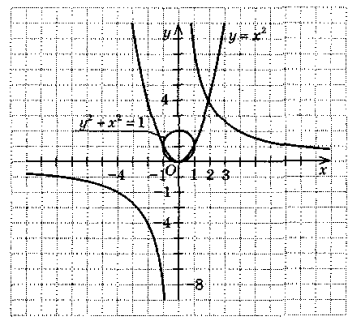
- За рисунком знайдіть розв’язки системи рівнянь:
1) 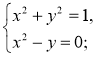
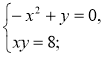
Письмові вправи
Для письмового розв’язання на уроці пропонуються вправи такого змісту:
- розв’язати графічно систему нелінійних рівнянь з двома змінними;
- за графіками знайти кількість розв’язків системи нелінійних рівнянь з двома змінними;
- на повторення: вправи на застосування різних способів розв’язування систем лінійних рівнянь з двома змінними та способів розв’язування квадратних рівнянь, а також рівнянь, що зводяться до квадратних (наприклад, шляхом введення нової змінної).
Розв’язування як письмових, так і усних вправ уроку, крім вироблення вмінь виконувати дії відповідно до алгоритму розв’язування системи рівнянь графічним способом, дає можли вість повторити велику кількість питань, вивчених у 7—9 класах (графіки функцій, перетворення виразів, а також геометричні пе ретворення графіків функцій). Для того щоб це повторення було більш ефективним, постійно слід вимагати від учнів усних комен тарів усіх побудов.
VII . Підсумки уроку
Контрольні запитання
- Що називають розв’язком системи рівнянь з двома змінними?
- Як знайти розв’язки системи рівнянь з двома змінними, використовуючи графіки цих рівнянь?
- Яку з наведених систем рівнянь можна розв’язувати за допомогою даного рисунка? Скільки розв’язків має ця система?
1) 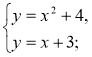
3) 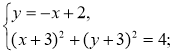
VIII . Домашнє завдання
- Вивчити зміст понять та алгоритмів уроку (див. опорний конспект № 19).
- Розв’язати вправи на застосування вивченого матеріалу (аналогічні вправам класної роботи).
- На повторення: розв’язати системи лінійних рівнянь з однією змінною (різними способами).
Источник
Тема 2. Системи лінійних рівнянь з двома змінними. Графічний спосіб розв’язування таких систем.
Розробка циклу уроків однієї з навчальних тем курсу алгебри „Системи лінійних рівнянь з двома змінними» для 7 класу. Другий урок із даної теми
Тема 2.
Системи лінійних рівнянь з двома змінними.
Графічний спосіб розв’язування таких систем.
Мета уроку: повторення та закріплення, уточнення та поглиблення попередньо засвоєних знань, умінь та навичок; сформувати поняття лінійних систем рівнянь з двома невідомими; навчити учнів наводити приклади; формування в учнів умінь розв’язувати системи рівнянь графічним способом; розгляд алгоритмів розв’язків систем.
Тип уроку: урок формування та вдосконалення вмінь та навичок
- Організаційний момент. Перевірка домашнього завдання.
- Актуалізація опорних знань та їх коригування. Написання самостійної роботи.
- Робота із електронним підручником(повтореня теоретичного матеріалу).
- Повідомлення теми і мети нового уроку.
- Мотивація навчальної діяльності.
- Розв’язування вправ(із подальшим поданням нового матеріалу та ознайомлення з правилами, алгоритмами виконання).
- Пробні та тренувальні вправи(використання вивченого в стандартних умовах).
- Закріплення вивченого матеріалу(використовуємо електронний підручник).
- Контроль і самоперевірка.
- Розв’язування вправ в нестандартних умовах. Робота у середовищі «Системи лінійних рівнянь» .
- Підбиття підсумків. Повідомлення домашнього завдання.
І, ІІ. Пивітання. Перевірка учнів. До дошки виходить учень і розв’язує домашні вправи, ззаду дошки ще двоє учнів пишуть відповідно І та ІІ варіант; решта пише самостійну роботу у робочих зошитах.
1. При яому значенні а пара чисел є розв’язком рівняння?
2х – 7у=а; 6х – ау=4
5х – 3у=а; 3х – ау=6
2. При якому значенні а графік рівняння проходить через початок координат?
3. Які з точок належать графіку рівняння?
4. Побудувати графік рівняння.
IV , V . Сьогодні, діти, ми з вами будемо вчити наступну тему, а саме: „Системи лінійних рівнянь з двома змінними. Використання графічного способу для їх розв’язання.” Для цього розглянемо такі вправи.
Задача. Сума двох чисел дорівнює 12, а їх різниця дорівнює 2. Знайдіть ці числа.
Позначимо перше число буквою х, а друге буквою у. Ва умовою задачі сума чисел дорівнює 12, тобто х + у = 12. Оскільки різниця чисел дорівнює 2, то х – у =2.
Ми склали два рівняння з двома змінними. Щоб від повісти на запитання задачі, треба знайти такі значення змінних, які перетворюють у правильну рівність кожне з рівнянь, тобто знайти спільні розв’язки цих рівнянь. У таких випадках говорять, що треба розв’язати систему рівнянь.
Систему рівнянь прийнято записувати за допомогою фігурної дужки. Складену за умовою задачі систему рів нянь можна записати так:
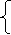
Пара значень змінних х=7, у=5 є розв’язком кож ного з рівнянь системи, оскільки обидві рівності 7+5=12 та 7 – 5= 2 правильні.
Таку пару називають розв’язком системи .
Означення . Розв’язком системи рівнянь з двома змінними називається пара значень змінних, що перетво рює кожне рівняння системи у правильну рівність.
Розв’язати систему рівнянь – означає знайти всі її розв’язки або довести, що розв’язків немає.
Щоб розв’язати систему лінійних рівнянь з двома змінними, можна використати графіки рівнянь.
Нехай треба розв’язати систему рівнянь
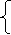
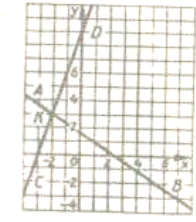
Координати будь-якої точки прямої АВ є розв’язком рівняння 2х + Зу =5, а координати будь-якої точки пря мої С D є розв’язком рівняння 2х – у = — 9. Координати точки перетину прямих задовольняють як перше рівняння, так і друге, тобто в розв’яз ком системи. Графіки перетинаються у точці К ( — 2; 3). Отже, система мав єдиний розв’язок х=-2, у =3.
Застосований нами спосіб розв’язу вання системи рівнянь називається графічним . Зауважимо, що гр афічний спосіб звичайно дає змогу знаходити розв’язки лише наближено.
Розглянемо системи двох лінійних рівнянь з двома змінними, у кожному з яких хоча б один з коефіцієнтів при змінних відмінний від нуля. З’ясуємо, чи завжди система має розв’язки і якщо має, то скільки. Графіками рівнянь системи є прямі. Якщо ці прямі перетинаються, то система має єдиний розв’язок, якщо прямі паралельні, то система не мав розв’язків, якщо прямі збігаються, то розв’язків безліч.
VI. Приклад 1 . З’ясуємо, скільки розв’язків мав систе ма рівнянь:
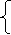
Розглянемо, яке взаємне розміщення графіків рівнянь нашої системи. Для цього виразимо з кожного рівняння у через х, дістанемо:
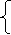
Рівняння у=-1,1х+12 та у=-6х+18 задаю ться лінійні функції. Кутові коефіцієнти прямих, які графіками цих функцій, різні. Отже, ці прямі перетинаються і система має єдиний розв’язок.
Приклад 2 . Розглянемо, скільки розв’язків має сис темі рівнянь:
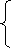
З кожного рівняння системи виразимо у через х:
Прямі, які в графіками лінійних функцій у=-0,4х+0,15 та у=-0,4х+3,2 паралельні, оскільки їхні кутові коефіцієнти однакові, а точки перетину з віссю у різні. Звідси випливає, що дана система рівнянь не має розв’язків.
Прик лад 3.
З’ясуємо, скільки розв’язків мав систе ма рівнянь
Виразивши з кожного рівняння системи у через х і діста немо:
Очевидно, що графіки рівнянь збігаються. Це означає, що будь-яка пара чисел (х; у), в якій х — довільне число, а у=-2,5 x — 9, є розв’язком системи. Система має без ліч розв’язків.
Розглянемо основні типи систем та їх розв ’ язки:
a , b , c , d – довільні раціональні числа, k – коеф і ц іє нт пропорц і йност і
Система не має розв’язків
Система не має розв’язків
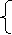
Будь-яка пара чисел – розвязок системи
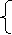
Система не має розв’язків
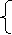
Розв ’ язок системи – координати будь-якої точки прямої
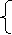
Єдиний розв ’ язок – координати точки перетину прямої
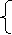
Система не має розв’язків
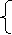
Координати будь-якої точки прямої є розвязками системи.
VII. Розглянемо дві задачі. Порівняємо їх зміст. З’ясуємо, що є спільного у змісті і способі розв’язання задач і чим вони різнять ся.
Задача 1. Човен йшов за течією зі швидкістю 15 км/год а проти течії — зі швидкістю 12 км/год. Визначте швидкість човна в стоячій воді та швид кість течії?
Якщо х — швидкість човна у стоячій воді, у — швидкість те чії, то згідно з умовою задачі дістаємо рівняння х + у = 15 і х — у = 12.
Оскільки потрібно знайти спільний розв’язок обох рівнянь, то потрібно знайти таку пару чисел (х, у), яка б задовольняла обидва рівняння.
Систему рівнянь записуємо так:
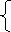
Задача 2. Сума двох чисел, дорівнює 15. Одне з них більше від другого на 12. Знайдіть ці числа.
Якщо одне з чисел по значити через х, а інше — че рез у, то згідно з умовою зада чі дістаємо рівняння х + у = 15 і х — у = 12.
Оскільки в цих рівняннях невідомі числа одні й ті ж, то ці рівняння повинні мати спільний розв’язок. У такому випадку ці рівняння утво рюють систему, яку записуємо так:
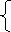
Фігурна дужка, що стоїть зліва, означає, що потрібно знайти таку пару чисел (х, у), яка б перетворювала обидва рівняння у правильні рівності.
Як бачимо, обидві задачі зводяться до знаходження такої пари значень змінних х і у, яка б задовольняла систему рівнянь:
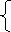
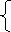
Систему рівнянь (І) можна розв’язати графічно.
Подумайте над запитаннями і дайте відповіді:
а) Де розміщені координати точок, що задовольняють рівняння х + у = 15 у першій задачі? у другій задачі? Чому?
б) Де розміщені координати точок, що є розв’язками другого рівняння х – у=12 у першій задачі? у другій задачі? Чому?
в) Що відображають координати точки R ?
Відповіді на поставлені запитання знайдіть у таких міркуваннях.
На перший погляд здається, що задачі різні. Задача 1 — з практичним змістом, вона є у підручнику з фізики; задача 2 — на знаходження чисел за їх сумою і різницею. Зі системи бачимо, що обидві задачі за структурою належать до задач на зна ходження чисел за їх сумою (х +у= 15) і різницею (х — у =12).
Проте, заглибившись у зміст кожної із задач, можна зауважити розбіжності між ними.
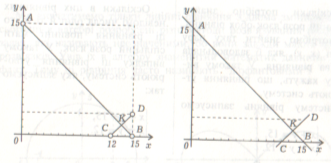
У задачі 1 перша частина речення «Човен йшов за течією річки зі швидкістю 15 км/год» описана відрізком АВ (крім точок А і В). Координати кожної його точки відображають власну швидкість човна і течії (х + у = 15), х > 0 і у > 0.
У задачі 2 перше речення «Сума двох чисел 15» описується прямою АВ (х + у = 1 5). Сума координат будь-якої точки прямої АВ дорівнює 15. Числа х і у — будь-які числа.
Друга частина речення першої задачі «а проти течії — зі швид кістю 12 км/год» зображена відрізком СВ(крім точок С D , х >0 і у > 0). Координати кожної його точки — це власна швидкість човна і течії річки.
У другій задачі друге речення «Одне з них більше від другого на 12» зображене не відрізком, а прямою С D .
Завдання першої задачі «Визначте швидкість човна в стоячій воді та швидкість течії?» збігається з вимогою другої задачі »Знай діть ці числа», оскільки відповіді на них вказуються координатами єдиної точки K . Ви також так гадаєте?
Чи кожна система двох рівнянь має тільки один розв’язок?
Звернемось до системи рівнянь задачі 2. Зміст цієї задачі відображений двома прямими АВ і С D . Координати точок прямої АВ дають усі розв’язки рівняння х + у = 15, а ко ординати точок прямої С D дають усі розв’язки рівняння х – у= 12.
Отже, якщо прямі АВ і С D перетинаються (в точці K ), то координати точки перетину є спільним розв ‘язком обидвох рівнянь, і система рівнянь у цьому випадку мас єдиний розв’язок. У розглянутих задачах 1 і 2 такою точкою була точка К (13,5; 1,5).
Якщо прямі АВ і С D збігаються, то координати будь-якої точки прямої АВ чи прямої С D є розв’язком системи рівнянь.
Задача № 3
Розв’язати систему рівнянь:
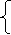
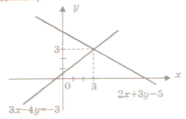
Будуємо графіки рівнянь, що входять до системи. Координати точки перетину є розв ’ язками системи. Графічний спосіб є зручним для знаходження числа розв’язків системи
х+3у=15 , у =5 — 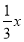
4у=3х+3, у= 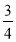
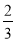
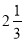
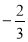
Графіки цих функцій перетинаються в точці з координаттами( 6 ; 3 ).
Задача №4
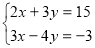
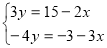
x
0
3
y
5
3
x
0
4
y
0,75
3,75
VIII .
IX . Самостійна робота(двоє учнів біля дошки розв’язують, решта – у зошитах. Здійснюється самоперевірка із подальшою перевіркою завдань з учнівськими роботами, що виконувалися біля дошки)
Источник


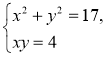 пара чисел:
пара чисел: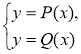 має три розв’язки. Скільки точок перетину мають графіки цих рівнянь?
має три розв’язки. Скільки точок перетину мають графіки цих рівнянь?