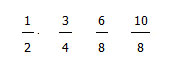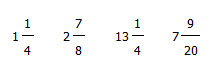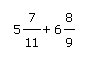Решите уравнение 453 x 153 90 двумя способами

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Немного теории.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2

Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0

Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^ = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Источник

Уравнения

Решение уравнений онлайн

Если вы это читаете, значит вас интересует вопрос решения уравнений.

Да, наши калькуляторы могут решить все уравнения, которые встречаются в школьном курсе и не только. Но нужно понимать, что большинство уравнений имеют несколько способов решения, а калькулятор выдает лишь только какое-то одно.

Бесспорно все способы решения хороши по-своему, но каждому методу отводится свое место в программе обучения.

Поэтому не стоит злоупотреблять калькуляторами, если ваш школьный учитель или личный репетитор требует решить уравнение одним способом, а вы предоставляете ему альтернативное решение.

Да, это может быть похвально, но опытный педагог сразу поймет, что решение уравнения не ваше.

Калькулятор решения уравнений

Калькулятор уравнений незаменимый помощник. Именно помощник, а не решатель проблем. Всегда старайтесь своими силами решать уравнения, а калькулятор используйте в качестве проверки вашего ответа.

Для грамотного учителя не столько важен конечный ответ, сколько сам ход решения уравнения.

Как вы могли заметить, при решении некоторых уравнений, например, квадратных, калькулятор может выполнить три разных способа решения. Это разложение уравнения на множители, выделение полного квадрата или найти корни уравнения через дискриминант.

Попытайтесь сначала самостоятельно решить заданное уравнение, вспомните чему вас учили на уроке.

Даже если вы ошибетесь в числах, то ничего страшного, ученик имеет право на ошибку, главное правильно мыслить.

С нашим калькулятором уравнений вы с легкостью исправите допущенную в вычислениях ошибку.

Источник

Решите паже 253-(x-459)=138

Ответ или решение 2

Для того, чтоб найти вычитаемое (х — 459) необходимо из уменьшаемого вычесть разницу. Для того, чтоб найти неизвестное уменьшаемое х необходимо к разнице прибавить вычитаемое.

х — 459 = 253 — 138;

Выполним проверку. Для этого необходимо найденное значение переменной подставить в исходное уравнение. Если правая сторона и левая сторона будут равны, тогда корень уравнения найден верно.

253 — (574 — 459) = 138;

Решим линейное уравнение 253 + (x — 459) = 138. Это уравнение можно решить двумя способами. Рассмотрим каждый из них.

Алгоритм решения линейного уравнения с одной переменной

• решим уравнение первым способом, используя правила нахождения неизвестного слагаемого и неизвестного уменьшаемого;
• решим уравнение вторым способом, используя тождественные преобразования;
• сделаем проверку найденного решения.

Первый способ решения уравнения

Посмотрим на наше уравнение 253 + (х – 459) = 138, как на сумму двух слагаемых, одно из которых (х – 459), а второе 253, а результатом сложения (суммой) является 138.

Вспомним правило, как найти неизвестное слагаемое.

Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

х – 459 = 138 – 253;

Выполним вычитание в правой части уравнения.

Теперь рассмотрим наше уравнение как разность. Где х — уменьшаемое, 459 — вычитаемое, а — 115 — разность.

Чтобы найти неизвестное уменьшаемое нужно к разности прибавить вычитаемое.

Второй способ решения уравнения

253 + (х – 459) = 138.

Откроем скобки в левой части уравнения, используя правило открытия скобок, перед которыми стоит знак плюс.

253 + х – 459 = 138;

Перенесем в правую часть уравнения слагаемые без переменной, при этом изменим их знак на противоположный.

х = 138 – 253 + 459;

Приведем подобные слагаемые в правой части уравнения, получим:

253 + (х – 459) = 138, подставим найденный корень.

Источник

5 класс. Математика. Виленкин. Учебник. Ответы к стр. 61

Ноя 19

5 класс. Математика. Виленкин. Учебник. Ответы к стр. 61

Натуральные числа
Сложение и вычитание натуральных чисел
Уравнение

Ответы к стр. 61

374. Составьте уравнение по рисунку 45 и решите его.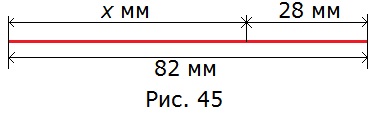

375. Решить уравнение (у + 64) — 38 = 48 можно двумя способами:
1) сначала найти неизвестное уменьшаемое у + 64:
у + 64 = 48 + 38, у + 64 = 86,
а потом найти неизвестное слагаемое у:
у = 86 — 64, у = 22 или
2) сначала упростить выражение, стоящее в левой части уравнения, использовав свойства вычитания:
у + 64 — 38 = 48, у + 26 = 48, а затем найти неизвестное слагаемое у:
у = 48 — 26, у = 22.
Подобным образом решите двумя способами уравнение:
а) (х + 98) + 14 = 169; б) (35 + у) — 15 = 31.

а) (х + 98) + 14 = 169, (х + 98) + 14 = 169,
х + 98 = 169 — 14, х + 98 + 14 = 169,
х + 98 = 155, х + 112 = 169,
х = 155 — 98, х = 169 — 112,
х = 57; х = 57;

б) (35 + у) — 15 = 31, (35 + у) — 15 = 31,
35 + у = 31 + 15, 35 + у — 15 = 31,
35 + у = 46, у + 20 = 31,
у = 46 — 35, у = 31 — 20,
у = 11; у= 11.

376. Решите уравнение и выполните проверку:
а) (х + 15) — 8 = 17; г) (у — 35) + 12 = 32;
б) (24 + х) — 21 = 10; д) 56 — (х + 12) = 24;
в) (45 — у) + 18 = 58; е) 55 — (х — 15) = 30.

а) (х + 15) — 8 = 17,
х + 15 = 17 + 8,
х + 15 = 25,
х = 25 — 15,
х = 10,
Проверка:
(10 + 15) — 8 = 17,
25 — 8 = 17,
17 = 17;

б) (24 + х) — 21 = 10,
24 + х = 10 + 21,
24 + х = 31,
х = 31 — 24,
х = 7,
Проверка:
(24 + 7) — 21 = 10,
31 — 21 = 10,
10 = 10;

в) (45 — у) + 18 = 58,
45 — у = 58 — 18,
45 — у = 40,
у = 45 — 40,
у = 5,
Проверка:
(45 — 5) + 18 = 58,
40 + 18 = 58,
58 =58;

г) (у — 35) + 12 = 32,
у — 35 = 32 — 12,
у — 35 = 20,
у = 20 + 35,
у = 55,
Проверка:
(55 — 35) + 12 = 32,
20 + 12 = 32,
32 = 32;

д) 56 — (х + 12) = 24,
56 — 24 = х + 12,
32 = х + 12,
х = 32 — 12,
х = 20,
Проверка:
56 — (20 + 12) = 24,
56 — 32 = 24,
24 = 24;

е) 55 — (х — 15) = 30,
55 — 30 = х — 15,
25 = х — 15,
х = 25 + 15,
х = 40,
Проверка:
55 — (40 — 15) = 30,
55 — 25 = 30,
30 = 30.

377. Решите с помощью уравнения задачу:
а) Витя задумал число. Если к этому числу прибавить 23 и к полученной сумме прибавить 18, то будет 52. Какое число задумал Витя?
б) Маша задумала число. Если к этому числу прибавить 14 и от полученной суммы отнять 12, то будет 75. Какое число задумала Маша?
в) В бензобак, где был бензин, перед поездкой долили ещё 39 л. Во время поездки израсходовали 43 л бензина, после чего в бензобаке осталось 27 л. Сколько литров бензина было в бензобаке первоначально?
г) В ателье было 60 м ткани. Из неё сшили платья, ещё 16 м израсходовали на детские костюмы, после чего осталось 20 м этой ткани. Сколько метров ткани пошло на платья?

Будем обозначать через х неизвестную величину.
а) (х + 23) + 18 = 52,
х + 23 = 52 — 18
х + 23 = 34,
х = 34 — 23,
х = 11.
О т в е т: задумано число 11.

б) (х + 14) — 12 = 75,
х + 14 = 75 + 12,
х + 14 = 87,
х = 87 — 14,
х = 73.
О т в е т: задумано число 73.

в) (х + 39) — 43 = 27,
х + 39 = 27 + 43,
х + 39 = 70,
х = 70 — 39,
х = 31.
О т в е т: был 31 л бензина.

г) (60 — х) — 16 = 20,
60 — х = 20 + 16,
60 — х = 36,
х = 60 — 36,
х = 24.
О т в е т: на платье пошло 24 м ткани.

Источник

Калькулятор дробей

Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.

Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.

Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.

Разновидности дробей:

Пример обыкновенных дробей:

Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:

1/2, 3/7, 19/5, 32/8, 10/100, 4/1

Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.

Пример десятичных дробей:

0,2, или 6,71 или 0,125

Смешанные дроби состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.

Пример смешанных дробей:

Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:

Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».

Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.

Вам нужно осуществить расчет примера:

После введения показателей в поля формы получаем:

Чтобы сделать самостоятельный расчет, введите данные в форму.

Источник