Решение задач кинематики. Задача «обгон»
Рассмотрим еще одну очень важную с практической точки зрения задачу. Пусть по прямой двухполосной дороге едут грузовик с прицепом и легковой автомобиль. Модули их скоростей равны соответственно |vг| = 20 м/с и |vл| = 30 м/с. Известно, что длина легкового автомобиля l1 = 5 м, а грузовик вместе с прицепом имеет длину l2 = 35 м. При этом легковой автомобиль, значение скорости которого больше, совершает обгон грузовика. Эта ситуация изображена на рис. 31.
Из сказанного ясно, что в задаче «обгон» принципиальную роль играют размеры тел. Поэтому для описания движения грузовика и легковушки нам надо выбрать конкретные точки этих тел. Кроме того, необходимо установить, какие моменты времени являются началом и окончанием обгона.
Моментом начала обгона (положение I) мы будем называть тот момент времени, когда самая передняя точка A («нос») легкового автомобиля поравнялась с самой задней точкой B («хвостом») прицепа грузовика. Моментом окончания обгона назовем тот момент времени, когда точка C (« хвост» ) легкового автомобиля поравняется с точкой D («носом») грузовика. Этот момент соответствует положению II на рис. 31.
Спрашивается:
1. В течение какого промежутка времени будет происходить обгон?
2. Какие расстояния проедут за время обгона легковой автомобиль и грузовик?
Чтобы ответить на поставленные вопросы, воспользуемся аналитическим методом решения кинематических задач.
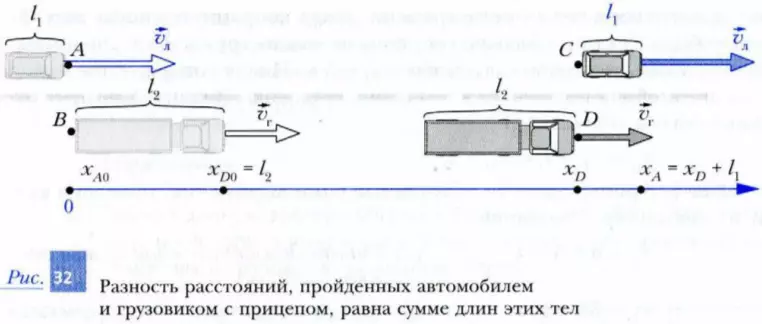
Шаг 1 . Введем систему отсчета (рис. 32). В качестве начала отсчета выберем камень, лежащий на обочине дороги напротив того места, где поравнялись точки A и B в момент начала обгона. Координатную ось X направим от этого камня параллельно дороге в сторону движения машин. В качестве единицы длины выберем 1 м. Часы (секундомер) включим в момент начала обгона.
По условию задачи грузовик и легковой автомобиль имеют конкретные размеры. Поэтому мы не можем считать наши тела точечными. Значит, для описания движения этих тел надо на каждом из них выбрать конкретные точки и далее следить за движением этих точек. В качестве точки, характеризующей положение легкового автомобиля, выберем точку A (его «нос»). Для описания положения грузовика с прицепом выберем точку D (соответственно «нос» грузовика). Теперь, если мы будем говорить, что координата легкового автомобиля равна, например, нулю, то это значит, что равна нулю координата его «носа» – точки A. А если мы скажем, что координата грузовика равна, например, сорока метрам, значит, говорится о координате «носа» грузовика – точке D. То есть мы будем следить за движением «носов» обоих движущихся тел.
Шаг 2 . Определим начальные координаты точек A и D, которые характеризуют положение соответственно легкового автомобиля и грузовика с прицепом. Из рис. 32 видно, что xA0 = 0, а xD0 = l2 = 35 м. Таким образом, в момент начала обгона «нос» грузовика опережает «нос» легкового автомобиля ровно на длину грузовика с прицепом l2 = 35 м.
Шаг 3 . В условии задачи даны модули скоростей легкового автомобиля и грузовика относительно дороги. При этом в выбранной системе отсчета координаты обоих тел увеличиваются. Следовательно, значения их скоростей положительны и равны соответственно vл = 30 м/с и vг = 20 м/с.
Шаг 4 . Напишем зависимости координат, точек A и D, от времени в выбранной системе отсчета:
Шаг 5 . Представим в виде уравнения условие окончания обгона. Если мы внимательно посмотрим на рис. 32 (положение II), то поймем, что обгон закончится в тот момент времени, когда координата «носа» легкового автомобиля xA станет больше координаты «носа» грузовика xD ровно на величину длины легкового автомобиля l1 = 5 м. Иначе говоря, «хвост» легкового автомобиля поравняется с «носом» грузовика. Значит, в момент окончания обгона (при t = tоб)
Шаг 6 . Запишем вместе полученные нами выражения, присвоив каждому из них номер и название:
xA = 0 + 30 · t, (1) (закон движения «носа» легкового автомобиля)
xD = 35 + 20 · t, (2) (закон движения «носа» грузовика)
xA = xD + 5. (3) (условие окончания обгона)
Шаг 7 . Решение уравнений.
Для нахождения момента времени, соответствующего окончанию обгона, подставим в уравнение (3) выражения для xA и xD из уравнений (1) и (2):
0 + 30 · t = 35 + 20 · t + 5,
30 · t — 20 · t = 35 + 5,
t = (35 + 5) / (30 — 20) = 4 (с).
Таким образом, через время tоб = 4 с после включения секундомера обгон будет завершен.
Найдем, какое расстояние прошел за это время «нос» легкового автомобиля (точка A). Для этого определим его координату в момент времени t = 4 с. Подставив данное значение времени в закон движения точки A, получим:
xA = 0 + 30 · t = 0 + 30 · 4 = 120 (м).
Так как начальная координата точки A xA0 = 0, «нос» автомобиля за время обгона прошел расстояние lA = 120 м.
Теперь определим, какое расстояние за время совершения обгона легковым автомобилем прошел грузовик. Для этого найдем координату его «носа» (точки D) в момент окончания обгона. Подставив значение времени окончания обгона t = 4 с в закон движения точки D, получим:
xD = 35 + 20 · 4= 115 (м).
Так как начальная координата «носа» грузовика равнялась xD0 = 35 м, то грузовик за время обгона прошел расстояние
Таким образом, разность пройденных «носом» легкового автомобиля (точкой A) и «носом» грузовика (точкой D) расстояний lA — lD = 120 — 80 = 40 (м), что составляет сумму длин обгоняемого и обгоняющего тел:
Упражнения
1. Решите данную задачу «обгон» табличным способом. Для этого, используя записанные в шаге 4 законы движения легкового автомобиля и грузовика, заполните таблицу.
2. Используя данные, полученные в предыдущем упражнении, или законы движения тел (шаг 4), постройте графики зависимости от времени координат точек A и D, характеризующих положения легкового автомобиля и грузовика. Укажите на графике точку (время и координату), в которой завершился процесс обгона.
3. Определите, в течение какого времени автобус длиной la = 20 м, движущийся с постоянной скоростью |va| = 35 м/с, будет обгонять грузовик длиной lг = 25 м, если скорость грузовика не изменяется и равна |vг| = 30 м/с. Задачу решите: а) аналитическим; б) табличным; в) графическим способами.
4. Зависит ли время обгона грузовика легковым автомобилем от размеров (длины) этих транспортных средств? Если зависит, то как?
Источник
Физика 7 класс
“Слышен собачий визг, Очумелов глядит в сторону и видит: из дровяного склада купца Пичугина, прыгая на трех ногах и оглядываясь, бежит собака. За ней гонится человек в ситцевой крахмальной рубахе и расстегнутой жилетке. Он бежит за ней и, подавшись туловищем вперед, падает на землю и хватает собаку за задние лапы. Слышен вторично собачий визг и крик: “Не пущай! ”. Из лавок высовываются сонные физиономии, и скоро около дровяного склада, словно из земли выросши, собирается толпа”.
Задача “погоня”. Скорость собаки на трех лапах – 5 м/с, а скорость человека в ситцевой крахмальной рубахе – 6 м/с Где человек в ситцевой рубахе поймал собаку, если первоначальное расстояние между ними было 3 м?
Шаг 1. Введем систему отсчета. В качестве тела отсчета выберем землю, а за начало отсчета – дровяной склад купца Пичугина, от которого начнет свое движение человек в ситцевой рубахе. Координатную ось направим вдоль дорожки в направлении движения собаки. Единица длины 1 м
Шаг 2. Определим начальные координаты движущихся тел человека и собаки. В момент включения секундомера начальная координата человека х0ч = 0, а собаки х0с = 3 м
Шаг 3. Найдем значения скоростей равномерного движения тел. В выбранной нами системе отсчета координата человек и собака будут увеличиваться, следовательно значения скоростей будут положительным vч = 6 м/с, vс = 5 м/с.
Шаг 4 (аналитический) . Запишем в аналитическом виде законы движения тел, учитывая известные данные:
Xч (t) = 0 + 6t Xс (t) = 3 + 5t
Шаг 5 (аналитический) . Представим в виде уравнения условие задачи – ситуацию, в которой человек “падает на землю и хватает собаку за задние лапы”. Это означает, что в некоторый момент времени их координаты совпадут:
хч (t) = xс (t)
Шаг 6 (аналитический) . Запишем вместе полученные в шагах 4 и 5 выражения, присвоив каждому из них свой номер и название:
Xч (t) = 0 + 6t – (1) закон движения человекаXс (t) = 3 + 5t – (2) закон движения собакиxч (t) = xс (t) – (3) условие встречи человека и собаки
Шаг 7 (аналитический) . Решение уравнений:
Xч (t) = xс (t)0 + 6t = 3 + 5t 6t – 5t = 3t = 3 (с)
Таким образом, человек “падает на землю и хватает собаку за задние лапы” через 3 с.
Для того чтобы определить, в каком месте это произойдет, подставим значение t=3с в один из законов движения тел. Например, в закон движения человека
xч (t) = 0 + 6.3 = 18(м)
Ответ: человек в ситцевой рубахе поймал собаку на расстоянии 18 м от дровяного склада купца Пичугина.
2 этап “основной”
Учитель
Ученики
Результат
Класс разбивается на группыКаждой группе предлагается одно из произведений А. П. Чехова по мотивам которого им предстоит составить и решить задачу. Метод решения (аналитический или графический группа выбирает сама) Читают предложенный отрывок из произведенияПредлагают свои варианты задачи.
Обсуждают.
Решают задачу
Делают соответствующие записи в тетради
Ещё одно знакомство с интересным и необычным способом прочтения литературного произведения. Осмысляют и углубляют знания.
Пример работы одной из групп. “На вокзале Николаевской железной дороги встретились два приятеля: один толстый, другой тонкий. Толстый только, что пообедал на вокзале, и его губы подернутые маслом, лоснились, как спелые вишни. Пахло от него хересом и флер-д оранжем. Тонкий же только что вышел из вагона и был навьючен чемоданами, узлами и картонками. Пахло от него ветчиной и кофейной гущей. ” (“Толстый и тонкий”)
Задача “встреча” По платформе навстречу друг другу идут два приятеля, давно не встречавшиеся. Скорость Толстого 2 м/с, он только что пообедал. Скорость Тонкого 3м/с, он мог бы идти и быстрее, но был “навьючен чемоданами, узлами и картонками”. В какой момент времени и где они встретятся, если первоначальное расстояние между ними 30м?
Источник
Презентация по физике «Решение задач кинематики»
Описание разработки
Цель: формирование умений решать задачи по предложенному алгоритму и объяснять полученные результаты.
1. Закрепить знания о способах описания прямолинейного равномерного движения (аналитический, графический, табличный);
2. Применить понятия и законы, описывающие прямолинейное равномерное движение при решении задач;
3. Уметь пользоваться алгоритмом при решении задач;
4. Развивать навыки самостоятельной работы при решении физических задач.
Пусть по прямолинейной дороге на встречу друг другу одновременно начинают двигаться пешеход и велосипедист. Расстояние между ними в момент начала движения составляет 20 м. При этом они движутся равномерно со скоростями, модули которых 3 м/с и 1 м/с соответственно.
Где произойдет встреча? И когда она состоится?
Шаг 1. Введем систему отсчета. Телом отсчета выберем землю, а за начало отсчета – дом, от которого начинает движение пешеход. Координатную ось направим вдоль движения пешехода. Будем считать пешехода и велосипедиста точечными телами.
Содержимое разработки
Решение задач кинематики
Скарлухина Майя Кирилловна , учитель физики
МБОУ «Средняя общеобразовательная школа №37 имени Новикова Гаврила Гавриловича» г.Кемерово
Пусть по прямолинейной дороге на встречу друг другу одновременно начинают двигаться пешеход и велосипедист. Расстояние между ними в момент начала движения составляет l=20м. При этом они движутся равномерно со скоростями, модули которых и соответственно.
Где произойдет встреча? И когда она состоится?
Шаг 1 . Введем систему отсчета. Телом отс-чета выберем землю, а за начало отсчета –дом, от которого начинает движение пе-шеход. Координатную ось направим вдоль движения пешехода. Будем считать пеше-хода и велосипедиста точечными телами.
Шаг 2 . Определим начальные координаты пешехода велосипедиста.
Шаг 3 . Найдем значения скоростей. В выбранной системе отсчета значение скорости пешехода положительно, а велосипедиста отрицательно.
Шаг 4. (Аналитический способ) Запишем законы движения тел, учитывая известные данные.
Шаг 5 . Запишем в виде уравнения условие задачи — встречу велосипедиста и пешехода
Шаг 6 . Решим полученные уравнения:
Встреча пешехода и велосипедиста состоится через 5 с после начала движения.
Определим координату точки , в которой
состоится встреча. Подставим значение
момента времени встречи в законы движения пешехода и велосипедиста:
Мы получили одинаковые значения координат для участников движения этой задачи.
При решении задач по кинематике графическим способом шаги 1, 2 и 3 повторяются: выбор СО, определение начальных координат и значений скорости движущихся тел.
Шаг 4 . Построим систему координат, состоящую из оси времени t и оси координаты Х. Отметим начальные координаты пешехода и велосипедиста.
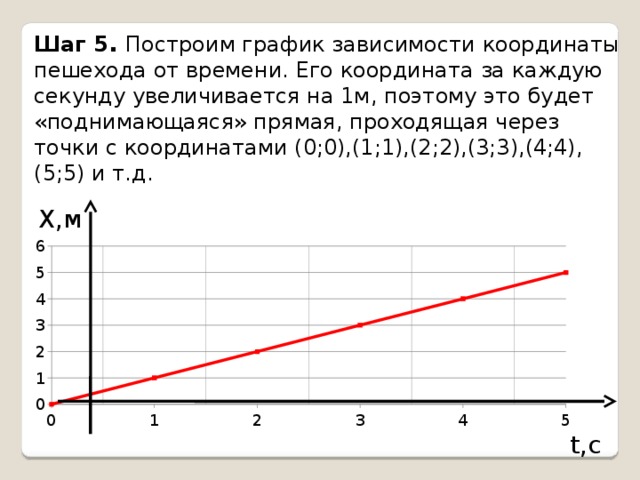
Шаг 5 . Построим график зависимости координаты пешехода от времени. Его координата за каждую секунду увеличивается на 1м, поэтому это будет «поднимающаяся» прямая, проходящая через точки с координатами (0;0),(1;1),(2;2),(3;3),(4;4), (5;5) и т.д.
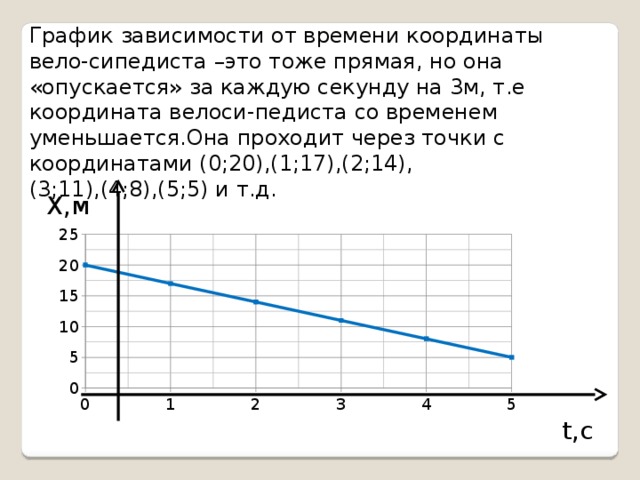
График зависимости от времени координаты вело-сипедиста –это тоже прямая, но она «опускается» за каждую секунду на 3м, т.е координата велоси-педиста со временем уменьшается.Она проходит через точки с координатами (0;20),(1;17),(2;14),
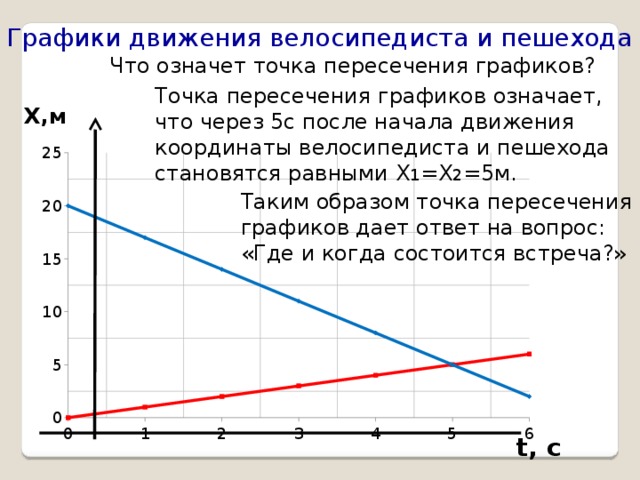
Графики движения велосипедиста и пешехода
Что означет точка пересечения графиков?
Точка пересечения графиков означает, что через 5с после начала движения координаты велосипедиста и пешехода становятся равными Х 1 =Х 2 =5м.
Таким образом точка пересечения графиков дает ответ на вопрос: «Где и когда состоится встреча?»
Рассмотрим задачу о погоне. По ровному полу в сторону своей норки по прямой бежит мышка со скоростью, модуль которой
. Вслед за мышкой гонится кот со скоростью . Поймает ли кот мышку, если расстояние между ними , а от мышки до ее норки .
Решите эту задачу аналитическим и графиче- ским способом, соблюдая пошаговое решение:
Шаг 1,2,3 Выбрать систему отсчета, определить начальные координаты тел и значения скорости для каждого тела.
Шаг 4. Записать уравнение координаты (закон движения) для каждого тела.
Шаг 5. Записать в виде уравнения условие встречи участников движения.
Шаг 6. Решить полученные уравнения совместно, найти время и координату места встречи.
Шаг 7. Построить систему координат, состоящую из оси времени t и оси координаты Х, отметить на ней начальные координаты тел.
Шаг 8. Построить график зависимости координаты от времени для каждого тела. Определить координату точки пересечения — время и место встречи.
Результаты решения данной задачи:
Начальные координаты и значения скорости
Время и место встречи
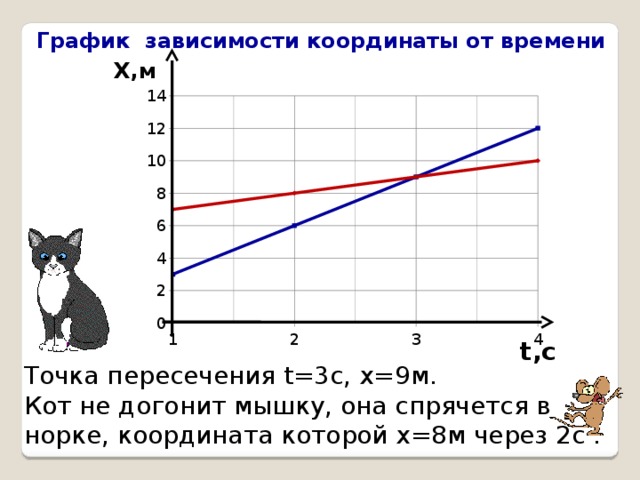
График зависимости координаты от времени
Точка пересечения t=3с, х=9м.
Кот не догонит мышку, она спрячется в норке, координата которой х=8м через 2с .
Спасибо за урок!
2.Грачев А.В., Погожев В.А., Селиверстов А.В.
Физика 7. Учебник. — М. Вентана – Граф.2012
Источник