- Конспект урока по теме «Решение квадратных уравнений разными способами» план-конспект урока по алгебре (8 класс) по теме
- Скачать:
- Предварительный просмотр:
- Как решать квадратные уравнения
- Понятие квадратного уравнения
- Приведенные и неприведенные квадратные уравнения
- Полные и неполные квадратные уравнения
- Решение неполных квадратных уравнений
- Как решить уравнение ax 2 = 0
- Как решить уравнение ax 2 + с = 0
- Как решить уравнение ax 2 + bx = 0
- Формула Виета
- Как разложить квадратное уравнение
- Дискриминант: формула корней квадратного уравнения
- Выводим формулу корней квадратного уравнения
- Алгоритм решения квадратных уравнений по формулам корней
- Примеры решения квадратных уравнений
- Формула корней для четных вторых коэффициентов
- Упрощаем вид квадратных уравнений
- Связь между корнями и коэффициентами
Конспект урока по теме «Решение квадратных уравнений разными способами»
план-конспект урока по алгебре (8 класс) по теме
Урок обобщения и систематизации знаний и умений учащихся. Углубленное изучение свойств квадратных уравнений. Решение квадратных уравнений ах²+вх+с=0, в которых а +в+с=0, а-в+с=0.
Скачать:
| Вложение | Размер |
|---|---|
| reshenie_kvadratnyh_uravneniy_raznymi_sposobami.doc | 228 КБ |
Предварительный просмотр:
Тема урока: «Решение квадратных уравнений разными способами»
Тип урока: Повторительно-обобщающий с углубленным изучением материала.
Жирнова Елена Евгеньевна
Тема урока: «Решение квадратных уравнений разными способами»
Тип урока : Урок обобщения и систематизации знаний и умений учащихся.
Углубленное изучение свойств квадратных уравнений.
- систематизировать знания по теме «Квадратные уравнения»;
- обеспечить закрепление теоремы Виета;
- обратить внимание учащихся на решение квадратных уравнений ах²+вх+с=0 , в которых а +в+с=0, а-в+с=0 ; привить навыки устного решения таких уравнений.
- способствовать выработке у учащихся желания и потребности обобщения изучаемых фактов;
- развивать самостоятельность и творчество;
- воспитывать аккуратность, доброжелательность, взаимопомощь;
- учить самоконтролю, взаимоконтролю.
- развивать внимание, логическое мышление, приемы сравнения, умение анализировать полученный результат, делать выводы, развивать математическую речь, память;
- способствовать развитию творческой активности учащихся, интереса к предмету.
Оборудование к уроку:
а) Квадратные уравнения. Неполные квадратные уравнения;
б) Полные квадратные уравнения. Способы решения;
в) Теорема Виета( прямая и обратная);
- учебник (Алгебра: учебник для 8 класса общеобразовательных учреждений. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров.
- карточки с заданиями;
- листы для записи ответов (для каждого учащегося).
- Оргмомент. Сообщение темы и целей урока.
- Актуализация опорных знаний и умений учащихся по теме «Решение квадратных уравнений».
- Изучение нового материала.
- Закрепление изученного.
- Проверка усвоения нового материала (самостоятельная работа).
- Инструктаж по выполнению домашнего задания.
- Итог урока и выставление оценок учащимся.
Диагностика умений и навыков учащихся:
- Распознавать среди множества уравнений квадратные.
- Выделять коэффициенты квадратного уравнения.
- Решать неполные квадратные уравнения.
- Определять количество корней неполного квадратного уравнения в зависимости от значения коэффициентов.
- Находить дискриминант квадратного уравнения по его коэффициентам.
- Определять наличие корней уравнения и их количество.
- Решать квадратные уравнения по общей формуле.
- Решать квадратные уравнения методом выделения квадрата двучлена.
- Выполнять приведение уравнения к виду ах²+вх+с=0 .
- Применять теорему Виета доля решения квадратных уравнений.
- Составлять квадратное уравнение по его корням.
- Оргмомент. Сообщение темы и целей урока.
Учитель дает установку на организованное начало урока, настраивает детей на серьезную, вдумчивую работу.
Тема нашего сегодняшнего урока: «Решение квадратных уравнений разными способами» (В тетради учащиеся записывают число, тему).
Целями нашего урока являются:
- Обобщение знаний по теме «Квадратные уравнения».
- Решение задач на применение прямой и обратной теоремы Виета.
- Изучение нового свойства квадратных уравнений (оно позволит нам устно и быстро находить корни некоторых квадратных уравнений).
Мы с вами уже научились решать разные виды квадратных уравнений (неполные, приведенные, полные), увидели, что многие уравнения, системы уравнений и задачи сводятся к решению квадратных уравнений. Поэтому очень важно уметь решать квадратные уравнения не только правильно, но и быстро. Некоторым приемам устного решения квадратных уравнений мы и должны сегодня научиться.
Например, нам нужно решить следующие уравнения (уравнения записаны на доске):
2013х 2 -1998х-15=0
2013х 2 +1997х-16=0
1998х 2 -2013х+15=0
1997х 2 +2013х+16=0
— Как можно решить данные уравнения?
— Сколько времени потребуется для этого?
— Обратите внимание на коэффициенты этих уравнений (они показывают ваш год рождения, возраст, настоящий год).
Оказывается, можно решить эти уравнения очень быстро! Уже в конце сегодняшнего урока каждый из вас сможет решить эти уравнения в уме за считанные секунды.
Рассмотрению способа решения таких уравнений будет посвящена часть нашего урока.
- Актуализация опорных знаний и умений учащихся.
Теперь повторим основной теоретический материал по теме «Квадратные уравнения» (работа с таблицами). В таблицах пунктирной линией обведены те записи, которые «открываются только по мере того, как учащиеся отвечают на соответствующие вопросы учителя.
— В каком случае уравнение вида ах²+вх+с=0 является квадратным?
— Какой вид примет это уравнение, если в=0, с=0; в=0, с≠0; в≠0, с=0? Как называются такие уравнения?
— Имеют ли корни уравнения ах²=0, ах²+с=0, ах²+вх=0 ? Приведите примеры таких уравнений.
— От какой величины зависит наличие действительных корней квадратного уравнения? Сколько корней могут иметь квадратные уравнения?
— Назовите формулу для нахождения дискриминанта квадратного уравнения.
— Какую формулу для нахождения корней вы знаете?
Давайте вспомним алгоритм решения квадратного уравнения по формуле.
На доске записано уравнение 7 х²-9х+2=0 . Решите эти уравнения в своих тетрадях. (1 чел. решает у доски с объяснением).
— Ребята, на доске записаны уравнения, определенные по какому-то признаку, как вы думаете, какое из уравнений этой группы является лишним?
а). 1) 2x² – x = 0 б). 1) x² – 5x + 1 = 0
2) x² – 16 = 0 2) 9x² – 6x + 10 = 0
3) 4x² + x – 3 =0 3) x² + 2x – 2 = 0
4) 2x² = 0 4) x² – 3x – 1 = 0
Ответы: а) 3) – лишнее, так как это полное квадратное уравнение
б) 2) – лишнее, так как 1, 3, 4 – приведенные квадратные уравнения
— Какое квадратное уравнение называется приведенным?
— Как можно решить приведенное квадратное уравнение? Вспомним теорему Виета и теорему, обратную теореме Виета.
— Как используется теорема Виета при решении уравнения вида ах²+вх+с=0 ?
— В приведенных уравнениях второй группы назовите, чему равна сумма корней и их произведение.
— Чему равна сумма корней второго уравнения? Чему равно произведение его корней?
Перед вами на парте лежат два листа: лист с заданиями на сегодняшний урок и лист ответов. Возьмите лист ответов, подпишите его.
Теперь выполним тестовое задание №1. На листе ответов вам нужно в первой таблице вписать цифру или знак, стоящий после правильного ответа в каждом задании. Приступайте.
1. Выберите среди квадратных уравнений приведенное.
Зх 2 — 7х + 6 = 0 (5),
х 2 — Зх — 2 = 0 (1),
-х 2 — 2х + 1 = 0 (4).
4х 2 — 17х +1 = 0 (5),
х 2 + 8х – 2 = 0 (1),
2. Для уравнения 7х 2 + 14х — 21 =0
2. Для уравнения 8х 2 -24х+ 16= 0
х 2 + 2х — 3 = 0 (5),
-х 2 -2х + 3 = 0 (6),
7х + 14x-21 = 0 (7).
х 2 — Зх + 2 = 0 (6),
-8х 2 + 24х — 16 = 0 (7).
3. Сумма корней уравнения х 2 — 5х — 6 = 0
- Сумма корней уравнения х 2 + 8х -7 = 0
- Произведение корней уравнения
х 2 + х — 2 = 0 равно
- Произведение корней уравнения
х 2 -2 х — 3 = 0 равно
5. Какое из уравнений имеет корни противоположных знаков
х 2 + 57х + 15,1 = 0 (-),
х 2 -4,1х + 3,5 = 0 (+),
х 2 — 18х — 0,48 = 0 ( . )?
Два человека (по одному от каждого варианта) выходят к доске и вписывают свои ответы в заранее подготовленную таблицу.
Источник
Как решать квадратные уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Есть три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Пифагора: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Выводим формулу корней квадратного уравненияПродолжим изучать формулу корней квадратного уравнения. Пусть перед нами есть задача решить квадратное уравнение ax 2 + bx + c = 0. Выполним ряд равносильных преобразований:
выделим полный квадрат левой части нового уравнения:
после чего уравнение примет вид перенесем два последних слагаемых в правую часть и сменим знак на противоположный: преобразуем выражение в правой части: Так, мы пришли к уравнению Отсюда выводы про корни уравнения И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D. По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: Источник |







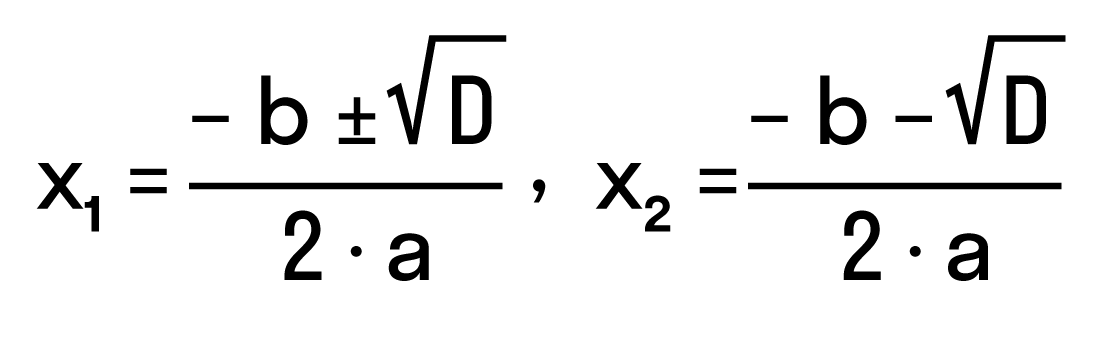
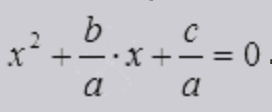
 ,
,
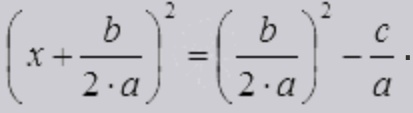

 , которое полностью равносильно исходному ax 2 + bx + c = 0.
, которое полностью равносильно исходному ax 2 + bx + c = 0.






