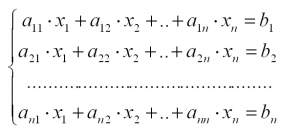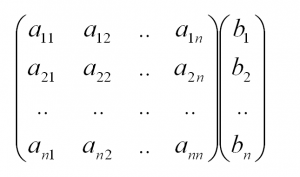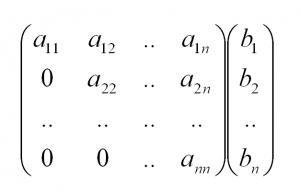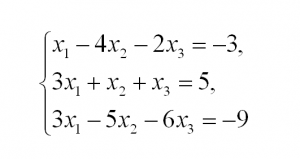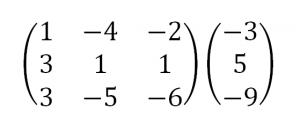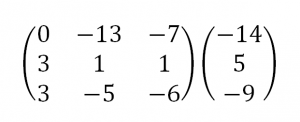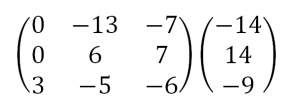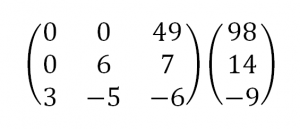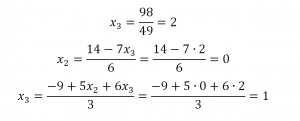Решить тремя способами метод гаусса

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

• перемена местами двух уравнений в системе,
• умножение какого-либо уравнения в системе на ненулевое действительное число,
• прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

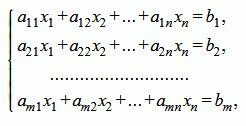(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

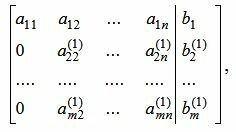(5)

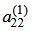
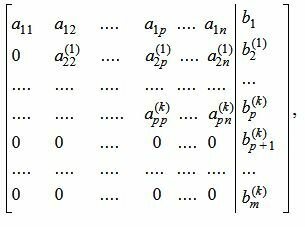На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 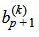. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

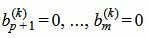
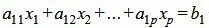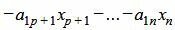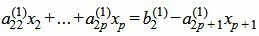Пусть . Тогда

(7)

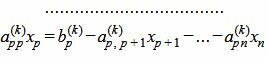Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

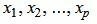
Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

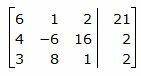Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

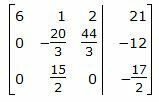Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

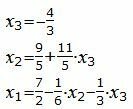Подставив верхние выражения в нижние, получим решение.

,,.

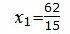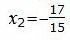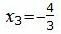Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

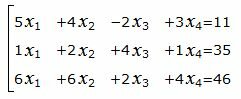Матричный вид записи: Ax=b, где

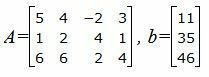Для решения системы, построим расширенную матрицу:

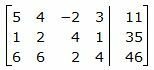Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

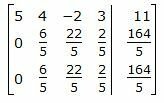Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

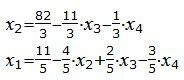где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

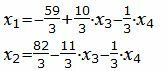где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

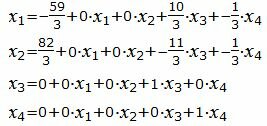Тогда векторное решение можно представить так:

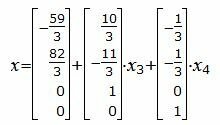где x₃, x₄− произвольные действительные числа.

Источник

Метод Гаусса для чайников: решаем СЛАУ легко

Сегодня разбираемся с методом Гаусса для решения систем линейных алгебраических уравнений. О том, что это за системы, можно почитать в предыдущей статье, посвященной решению тех же СЛАУ методом Крамера. Метод Гаусса не требует каких-то специфических знаний, нужна лишь внимательность и последовательность. Несмотря на то что с точки зрения математики для его применения хватит и школьной подготовки, у студентов освоение этого метода часто вызывает сложности. В этой статье попробуем свести их на нет!

Метод Гаусса

Метод Гаусса – наиболее универсальный метод решения СЛАУ (за исключением ну уж очень больших систем). В отличие от рассмотренного ранее метода Крамера, он подходит не только для систем, имеющих единственное решение, но и для систем, у которых решений бесконечное множество. Здесь возможны три варианта.

1. Система имеет единственное решение (определитель главной матрицы системы не равен нулю);
2. Система имеет бесконечное множество решений;
3. Решений нет, система несовместна.

Итак, у нас есть система (пусть у нее будет одно решение), и мы собираемся решать ее методом Гаусса. Как это работает?

Метод Гаусса состоит из двух этапов – прямого и обратного.

Прямой ход метода Гаусса

Сначала запишем расширенную матрицу системы. Для этого в главную матрицу добавляем столбец свободных членов.

Вся суть метода Гаусса заключается в том, чтобы путем элементарных преобразований привести данную матрицу к ступенчатому (или как еще говорят треугольному) виду. В таком виде под (или над) главной диагональю матрицы должны быть одни нули.

Что можно делать:

1. Можно переставлять строки матрицы местами;
2. Если в матрице есть одинаковые (или пропорциональные) строки, можно удалить их все, кроме одной;
3. Можно умножать или делить строку на любое число (кроме нуля);
4. Нулевые строки удаляются;
5. Можно прибавлять к строке строку, умноженную на число, отличное от нуля.

Обратный ход метода Гаусса

После того как мы преобразуем систему таким образом, одна неизвестная Xn становится известна, и можно в обратном порядке найти все оставшиеся неизвестные, подставляя уже известные иксы в уравнения системы, вплоть до первого.

Когда интернет всегда под рукой, можно решить систему уравнений методом Гаусса онлайн. Достаточно лишь вбить в онлайн-калькулятор коэффициенты. Но согласитесь, гораздо приятнее осознавать, что пример решен не компьютерной программой, а Вашим собственным мозгом.

Пример решения системы уравнений методом Гаусс

А теперь — пример, чтобы все стало наглядно и понятно. Пусть дана система линейных уравнений, и нужно решить ее методом Гаусса:

Сначала запишем расширенную матрицу:

Теперь займемся преобразованиями. Помним, что нам нужно добиться треугольного вида матрицы. Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой и получим:

Затем умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Умножим 1-ую строку на (6). Умножим 2-ую строку на (13). Добавим 2-ую строку к 1-ой:

Вуаля — система приведена к соответствующему виду. Осталось найти неизвестные:

Система в данном примере имеет единственное решение. Решение систем с бесконечным множеством решений мы рассмотрим в отдельной статье. Возможно, сначала Вы не будете знать, с чего начать преобразования матрицы, но после соответствующей практики набьете руку и будете щелкать СЛАУ методом Гаусса как орешки. А если Вы вдруг столкнетесь со СЛАУ, которая окажется слишком крепким орешком, обращайтесь к нашим авторам! Заказать недорого реферат вы можете, оставив заявку в Заочнике. Вместе мы решим любую задачу!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник