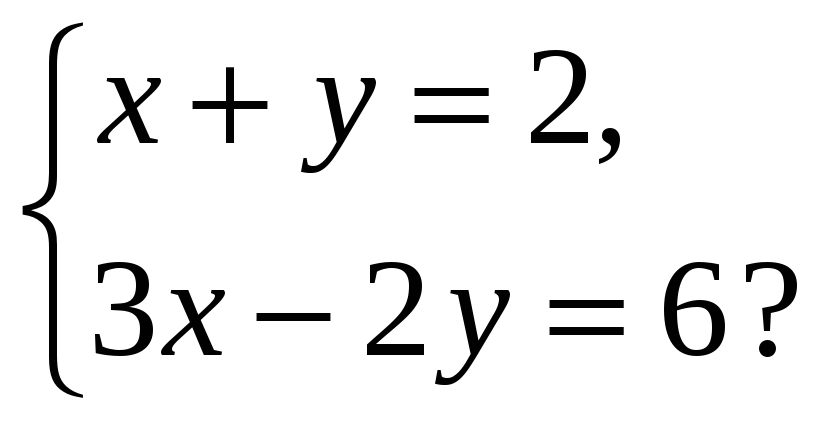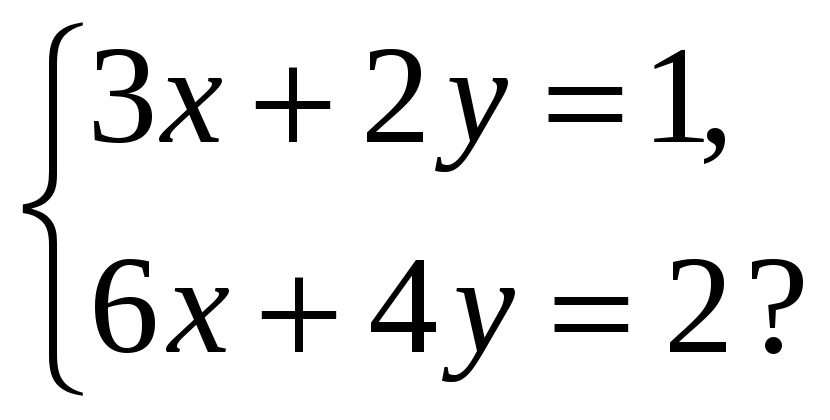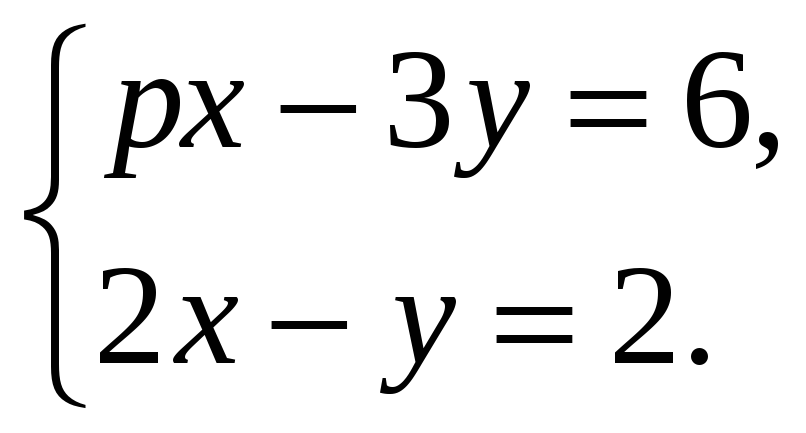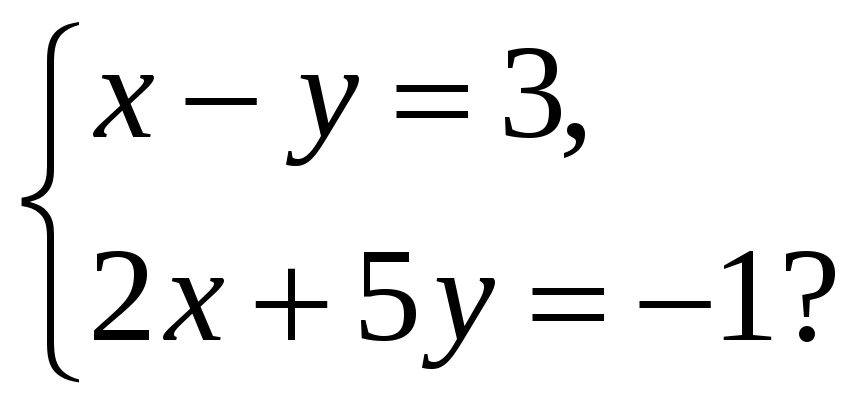- Решить систему графическим способом самостоятельная
- Графический метод
- Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Видео YouTube
- Проверочная работа по теме Графический способ решения СЛУ 7 класс
- Просмотр содержимого документа «Проверочная работа по теме Графический способ решения СЛУ 7 класс»
- Самостоятельная работа по теме «уравнения с двумя переменными и его график»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Решить систему графическим способом самостоятельная
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим способом систему уравнений.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Пример 5

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
Источник
Проверочная работа по теме Графический способ решения СЛУ 7 класс

Проверочная работа по теме Графический способ решения СЛУ 7 класс
Просмотр содержимого документа
«Проверочная работа по теме Графический способ решения СЛУ 7 класс»
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 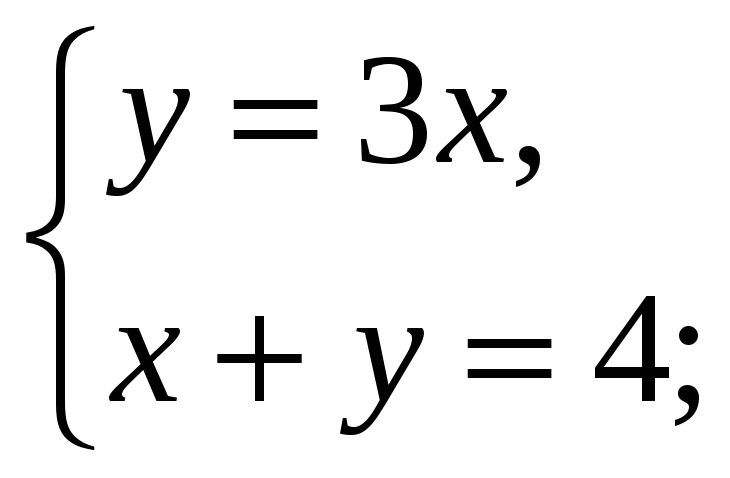
3. Сколько решений имеет система уравнений
а) 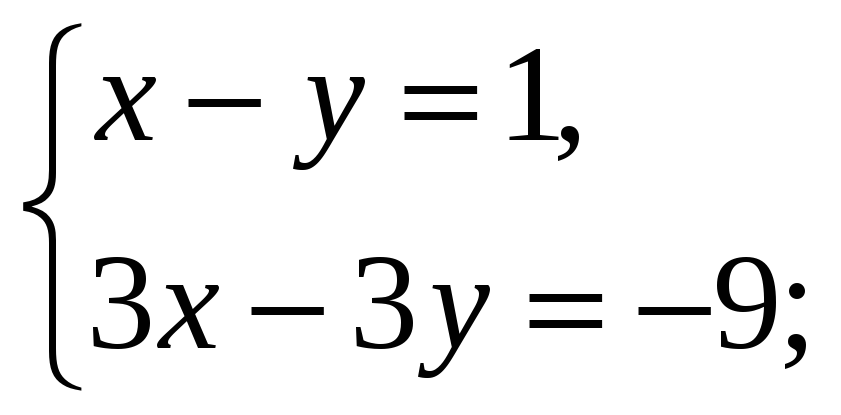
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 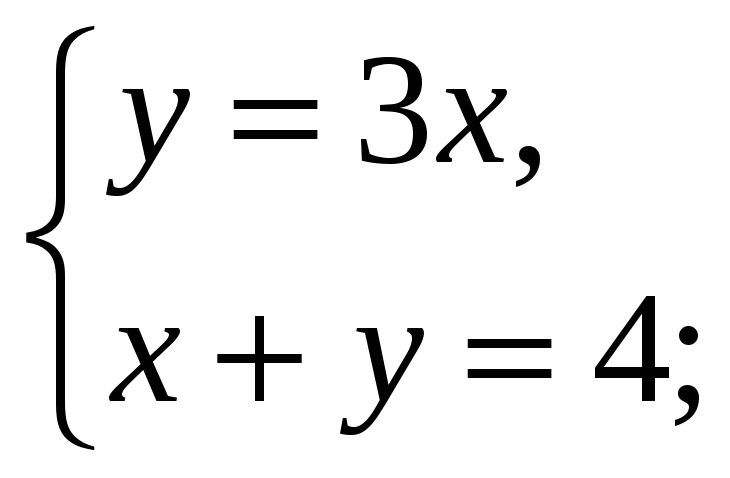
3. Сколько решений имеет система уравнений
а) 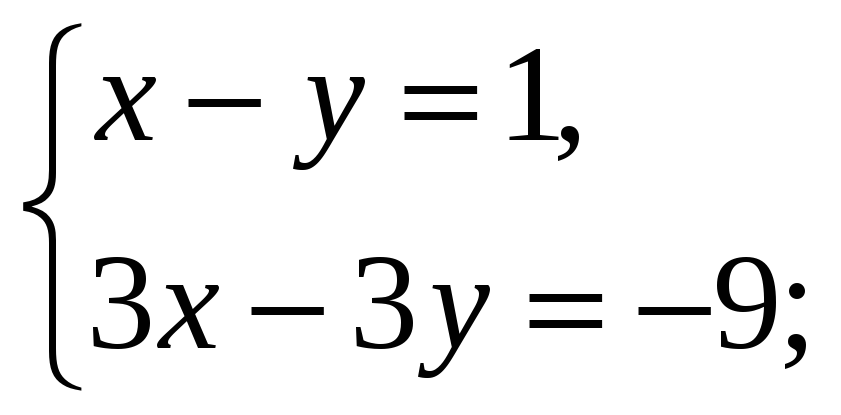
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных пар чисел (- 6; 8), (0; — 3), (2; 0) является решением данной системы уравнений 
2. Решите графически систему уравнений
а) 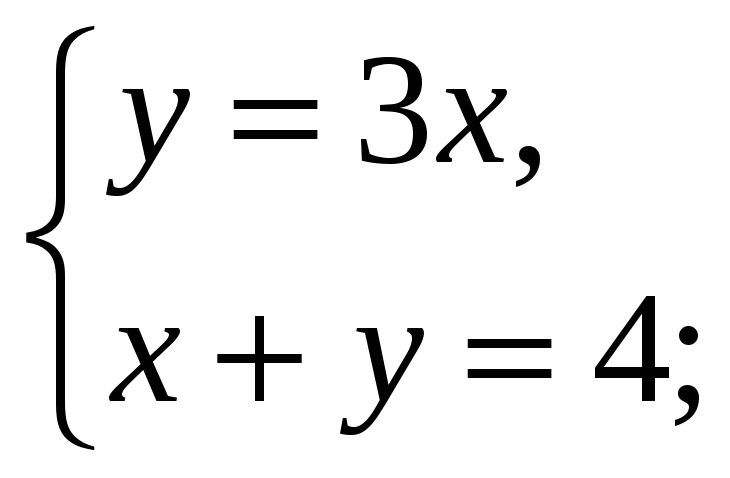
3. Сколько решений имеет система уравнений
а) 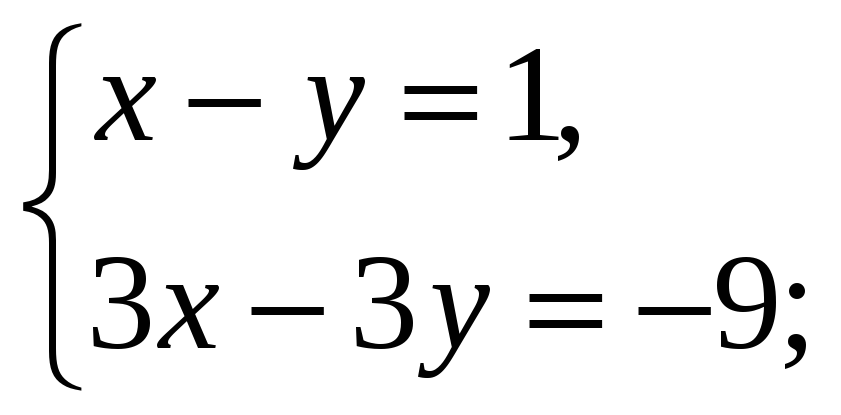
4. Напишите какую-либо систему уравнений, имеющую решение (4; 3).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 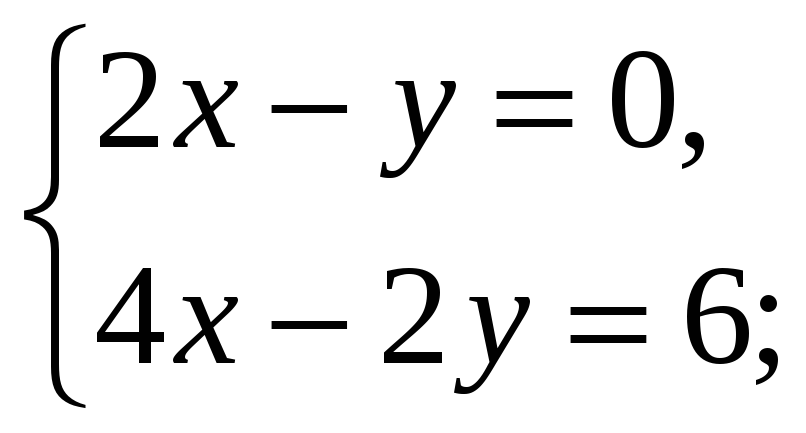
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 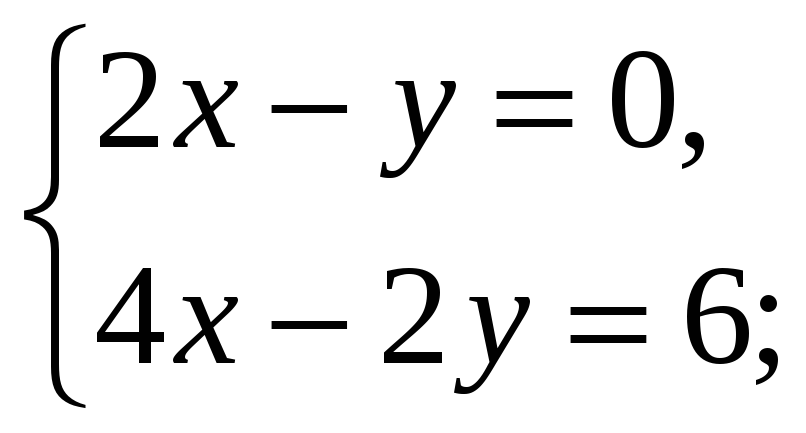
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
1. Какая из заданных из пар чисел (7; — 3), (2; — 1), (3; 0) является решением данной системы уравнений
2. Решите графически систему уравнений
а) 
3. Сколько решений имеет система уравнений
а) 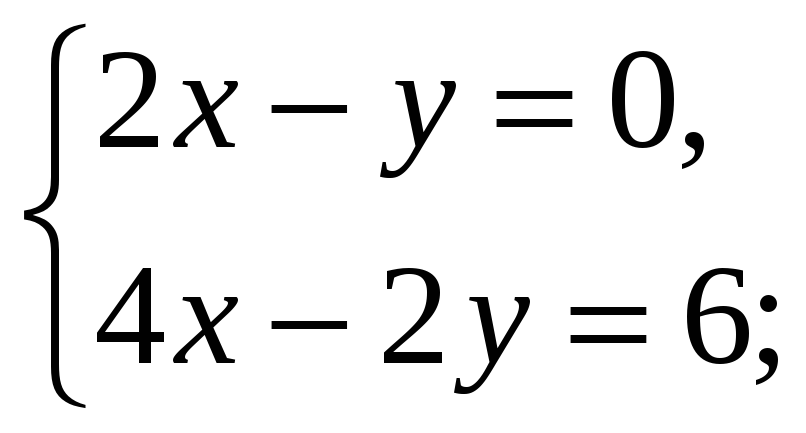
4. Напишите какую-либо систему уравнений, имеющую решение (5; -1).
5. Подберите, если возможно, такое значение р, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений:
Источник
Самостоятельная работа по теме «уравнения с двумя переменными и его график»
Выбранный для просмотра документ Самостоятельная.docx
№1. Каким из уравнений принадлежит точка с координатами (2;4):



№2. Постройте график функции:


№3. Составьте уравнение, графиком которого является пара прямых:
Запишите уравнение окружности с центром в начале координат, зная, что она проходит через точку:
Напишите уравнение окружности, зная, что её центр находится в точке К (1;-2) и она проходит через точку А(-1;1), В(-3;7).
№1. Каким из уравнений принадлежит точка с координатами (2;4):



№2. Постройте график функции:


№3. Составьте уравнение, графиком которого является пара прямых:
Запишите уравнение окружности с центром в начале координат, зная, что она проходит через точку: 
Напишите уравнение окружности, зная, что её центр находится в точке К (2;-1) и она проходит через точку А(-2;2), В(1;-4).
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 813 человек из 76 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 287 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 599 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-328716
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Москве запустили онлайн-проект по борьбе со школьным буллингом
Время чтения: 2 минуты
Руководители управлений образования ДФО пройдут переобучение в Москве
Время чтения: 1 минута
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник