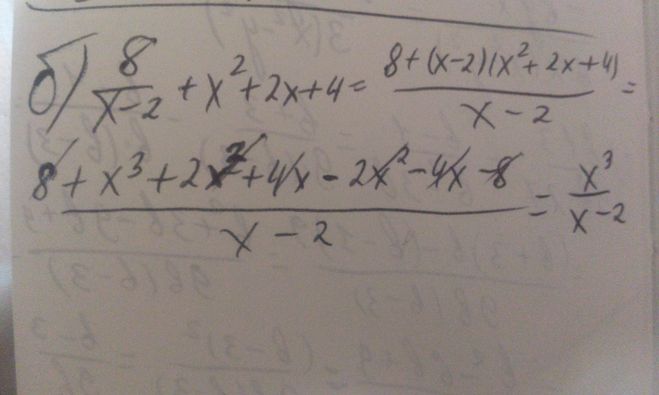Решение текстовых задач арифметическим способом
Разделы: Математика
Обучение решению текстовых задач играет важную роль в формировании математических знаний. Текстовые задачи дают большой простор для развития мышления учащихся. Обучение решению задач – это не только обучение технике получения правильных ответов в некоторых типичных ситуациях, сколько обучение творческому подходу к поиску решения, накопление опыта мыслительной деятельности и демонстрация учащимися возможностей математики в решении разнообразных задач. Однако при решении текстовых задач в 5-6 классах чаще всего используется уравнение. Но мышление пятиклассников еще не готово к формальным процедурам, выполняемым при решении уравнений. Арифметический способ решения задач имеют ряд преимуществ по сравнению с алгебраическим потому, что результат каждого шага по действиям нагляднее и конкретнее, не выходит за рамки опыта пятиклассников. Школьники лучше и быстрее решают задачи по действиям, чем с помощью уравнений. Детское мышление конкретно, и развивать его надо на конкретных предметах и величинах, затем постепенно переходить к оперированию абстрактными образами.
Работа над задачей предусматривает внимательное прочтение текста условия, вникания в смысл каждого слова. Приведу примеры задач, которые легко и просто можно решить арифметическим способом.
Задача 1. Для приготовления варенья на две части малины берут три части сахара. Сколько килограммов сахара нужно взять на 2 кг 600 г малины?
При решении задачи на “части” надо приучить наглядно представлять условие задачи, т.е. лучше опираться на рисунок.
- 2600:2=1300 (г) — приходится на одну часть варенья;
- 1300*3= 3900 (г) — сахара нужно взять.
Задача 2. На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках вместе стояло 120 книг. Сколько книг стояло на каждой полке?
1) 1+3=4 (части) — приходится на все книги;
2) 120:4=30 (книг) — приходится на одну часть ( книги на второй полке);
3) 30*3=90 (книг)- стояло на первой полке.
Задача 3. В клетке сидят фазаны и кролики. Всего в ней 27 голов и 74 ноги. Узнать число фазанов и число кроликов в клетке.
Представим, что на крышку клетки, в которой сидят фазаны и кролики, мы положили морковку. Тогда все кролики встанут на задние лапки, чтобы дотянуться до нее. Тогда:
- 27*2=54 (ноги) — будут стоять на полу;
- 74-54=20 (ног) — будут наверху;
- 20:2=10 (кроликов);
- 27-10=17 (фазанов).
Задача 4. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, а в кино – 21, а 5 человек не ходили ни на экскурсию, ни в кино. Сколько человек ходили и на экскурсию, и в кино?
Для анализа условия и выбора плана решения можно использовать “круги Эйлера”.
- 30-5=25 (человек) – ходили или в кино, или на экскурсию,
- 25-23=2 (человек) – ходили только в кино;
- 21-2=19 ( человек) – ходили и в кино, и на экскурсию.
Задача 5. Три утенка и четыре гусенка весят 2 кг 500 г, а четыре утенка и три гусенка весят 2кг 400г. Сколько весит один гусенок?
- 2500+2400=2900 (г) – весят семь утят и семь гусят;
- 4900:7=700 (г) – вес одного утенка и одного гусенка;
- 700*3=2100 (г) – вес 3 утят и 3 гусят;
- 2500-2100=400 (г) – вес гусенка.
Задача 6. Для детского сада купили 20 пирамид: больших и маленьких – по 7 и по 5 колец. У всех пирамид 128 колец. Сколько было больших пирамид?
Представим, что со всех больших пирамид мы сняли по два кольца. Тогда:
1) 20*5=100 (колец) – осталось;
2) 128-100-28 (колец) – мы сняли;
3) 28:2=14 (больших пирамид).
Задача 7. Арбуз массой 20кг содержал 99% воды. Когда он немного усох, содержание воды в нем уменьшилось до 98%. Определите массу арбуза.
Для удобства решение будет сопровождаться иллюстрацией прямоугольников.
| 99% вода | 1% сухое вещество |
| 98% вода | 2% сухое вещество |
При этом желательно рисовать прямоугольники “сухого вещества” равными, потому что масса “сухого вещества” в арбузе остается неизменной.
1) 20:100=0,2 (кг) – масса “сухого вещества”;
2) 0,2:2=0,1 (кг) – приходится на 1% усохшего арбуза;
3) 0,1*100=10 (кг) – масса арбуза.
Задача 8. Гости спросили: сколько лет исполнилось каждой из трех сестер? Вера ответила, что ей и Наде вместе 28 лет, Наде и Любе вместе 23 года, а всем троим 38 лет. Сколько лет каждой из сестер?
- 38-28=10 (лет) – Любе;
- 23-10=13 (лет) – Наде;
- 28-13=15 (лет) – Вере.
Арифметический способ решения текстовых задач учит ребенка действовать осознанно, логически правильно, потому что при решении таким способом усиливается внимание к вопросу “почему” и имеется большой развивающий потенциал. Это способствует развитию учащихся, формированию у них интереса к решению задач и к самой науке математике.
Чтобы сделать обучение посильным, увлекательным и поучительным, надо очень внимательно отнестись к выбору текстовых задач, рассматривать различные способы их решения, выбирая оптимальные из них, развивать логическое мышление, что в дальнейшем необходимо при решении геометрических задач.
Научиться решать задачи школьники смогут, лишь решая их. “Если вы хотите научиться плавать, то смело входите в воду, а, если хотите научиться решать задачи, то решайте их”,- пишет Д.Пойа в книге “ Математическое открытие”.
Источник
Конспект урока по математике на тему «Алгебраический и арифметический способы решения задач» (4 класс)
Государственное автономное образовательное учреждение
«Саратовский областной педагогический колледж»
Конспект урока по математике
«Алгебраический и арифметический способы решения задач.»
Студентка 3го курса 30й группы
Методист: Попова Е.И. ________________
Учитель: Емелина Л.А.____________________
Дата проведения: 28.04.2021
Тема урока: «Алгебраический и арифметический способы решения задач.»
Тип урока: повторение знаний.
Цель: пополнение знаний учащихся о решении задач с помощью уравнений, научить подбирать арифметическое или алгебраическое решение задачи.
Образовательные: отрабатывать знания, умения, навыки у детей в решении задач, используя уравнения.
Развивающие: развивать внимание, логическое мышление.
Воспитательные: воспитывать уважение к мнению других людей, чувство взаимовыручки.
Проявлять интерес к учебному материалу.
Контролирование своей деятельности по ходу и через результат выполнения задания, определение последовательности действий, умение планировать работу.
Создание и нахождение путей выхода из проблемной ситуации; выполнение действий по заданному алгоритму.
Оборудование: учебник, рабочая тетрадь.
средства, интерактивное оборудование
к занятию на уроке.
-Здравствуйте, дорогие ребята! Меня зовут Юлия Александровна, и сегодня я проведу у вас урок математики.
Мы пришли сюда учиться,
Не лениться, а трудиться.
Проверяют готовность к уроку.
2. Мотивация к учебной деятельности
Выработка внутренней готовности выполнения нормативных требований учебной деятельности.
Наш девиз урока:
«Всякая хорошо решённая задача доставляет умственное наслаждение»
— Сегодня на уроке мы закрепим умения решать задачи арифметическим и алгебраическим путём.
3. Актуализация знаний
подготовка мышления учащихся, организация осознания ими внутренней потребности к построению учебных действий .
Устный счёт, посмотрите на доску, НАЧИНАЕМ СЧИТАТЬ
Запишите сегодняшнее число, классная работа. Откройте учебники на странице 92, найдите номер 447 что надо сделать?
-Один желающий выходит к доске, с остальными работаем на местах.
-Первое действие? Второе? Третье?
-Решаем второе выражение, один желающий к доске.
-Решаем третье выражение, один желающий к доске.
— Решаем четвёртое выражение, один желающий к доске.
-Теперь нам нужно изменить порядок действий в каждом выражении так, чтобы их значения не изменились.
Найти значение выражения
(242 526+18354) :(15*4)=4 348
1)242 526+18 354=260 880
3) 260 880: 60 =4 348
4. Выявление места и причины затруднения
организовать анализ учащимися возникшей ситуации и на этой основе выявить места и причины затруднения, осознать то, в чем именно состоит недостаточность их знаний, умений или способностей.
Танграм (от китайского «семь дощечек мастерства») состоит из семи плоских фигур. Их необходимо сложить определенным образом для получения более сложной фигуры, изображающей человека, животное, растение, предмет, цифру, букву и т.д. Условиями игры являются использование всех семи фигур танграма и отсутствие наложения между фигурами. Начинать сложение головоломки следует с нахождения местоположения самого большого треугольника.
Танграм считается древней игрой, возникшей более 4000 лет назад. По легенде у одного человека выпала из рук и разбилась фарфоровая плитка. Получилось 7 частей, и расстроенный человек попытался поскорее сложить их снова в единое целое, но результатом стало появление разнообразных фигур. Занятие оказалось очень увлекательным, впоследствии оно превратилось в игру и нашло множество поклонников.
Источник
В чем отличие арифметического от алгебраического способа решения задач?
Арифметический — это по сути способ рассуждений. А алгебраический — это составление уравнений.
Вот возьмем для примера знаменитую задачу из рассказа Чехова «Репетитор».
Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?
Алгебраический способ такой:
Пусть купец купил x аршин синего и y аршин черного сукна.
Решаем систему и получаем
А арифметический способ такой. Представим себе, что он купил только черное сукно, все 138 аршин по 3 руб.
Тогда он заплатил бы 138*3 = 414 руб. А он заплатил 540 руб. Значит, остальные 540-414=126 руб. он заплатил за синее сукно.
Синее стоит дороже на 2 руб за каждый аршин. А он заплатил лишних 126 руб.
Значит, он купил 126/2 = 63 аршина синего сукна. Тогда черного он купил 138 — 63 = 75 аршин.
И очень жаль, что в школе постепенно отказываются от арифметического способа и всё решают уравнениями.
Кстати, в рассказе репетитор — сам ученик 7 класса — как раз не знал арифметического способа и не смог решить эту задачу, хотя она для 3 класса. А иксов ученик в 3 классе еще не проходил.
В арифметике с применением конкретных чисел записанных только цыфрами. А в алгебре вы решаете задачи с неизвестными числами, обобщённые значения которых выражены символами в виде латинских букв.
Затем уже в решение из символов (букв) вы можете подставить конкретные числа выраженные цыфрами и решить уже ставшую конкретной арифметическую задачу.
Проще сказать отличие в следующем:
В арифметической задаче вы ищите конкретный числовой ответ, а в алгебраической задаче вы ищите обобщённый ответ для всех возможных числовых значений выраженный в алгебраических символах.
Часто родители,а иногда и ученики,задают «хитрые» задачки для 2-3 класса,все начинают помогать через х и у ,а родители говорят:»ну как ребёнку объяснить эти иксы.А задача решается просто арифметическим способом.Простой пример:На почте приняли 7 больших посылок, каждая массой 9 кг, и 5 маленьких. Какова масса маленькой посылки, если масса всех посылок получилась 78 кг?Арифметический способ:7*9=63кг,2)78-63=15 кг 3)15\5=3(кг)-масса маленькой посылки.Алгебраический способ:х-вес маленькой посылки.уравнение:5х+7*9=78,х=3,но чаще бывают более сложные задачи,эта наипростейшая.Но смысл тот же.
Это уравнение является линейным, поэтому для его решения необходимо:
1) Раскрыть скобки в левой и в правой части.
2) Привести подобные слагаемые.
3) Слагаемые с x перенести в левую часть, числовые слагаемые перенести в правую часть.
Итак, решим уравнение 0,4 (3x — 0,5) = 1,5x + 0,2 (x + 1).
0,4 * 3x — 0,4 * 0,5 = 1,5x + 0,2x + 0,2.
1,2x — 0,2 = 1,7x + 0,2.
Значит, корень уравнения x = -0,8.
0,4 * (3 * (-0,8) — 0,5) = 1,5 * (-0,8) + 0,2 (-0,8 + 1).
0,4 * (-2,9) = -1,2 + 0,04.
Верно. Значит, корень данного уравнения был найден правильно.
Вас нужно лишь применить правила приведения дробей, раскрытие скобок и сумма квадратов.
1) Умножаем правую часть, чтобы получить дробь. Раскрываем скобки и приводим подоные члены.
2) Действуем аналогично, обращая внимания на знаки. Заметим, что (x-y)*(x+y)=x^2-y^2
3) Можем вынести 9 за скобки, а во второй дроби b. Тогда будет легче привести к общему знаменателю.
Пусть V — скорость автобуса, t — время в часах, за который автобус догнал первого велосипедиста.
Автобус проехал за t часов столько же, сколько велосипедист за t+1 час, расстояние равно скорость умножить на время, считаем и приравниваем расстояния, которые проехали автобус и первый велосипедист, получаем
Второго велосипедиста автобус догнал через 10 минут = 1/6 часа после того, как первого, то есть через t+1/6 часов после начала своего движения, второй велосипедист к тому времени ехал 1+t+1/6 часов, делаем то же самое, что для первого велосипедиста, получаем
Итак, у нас есть система из двух уравнений с двумя неизвестными
Вычтем из второго первое, получим
1/6V=5(1+t)+20/6, домножим обе части на 6, получим V=30(1+t)+20, упростим, получим V=30t+50, подставим в первое уравнение:
30t^2+50t=15+15t, где t^2 — это t в квадрате. Перенесём всё в одну часть и сократим на 5, получим
Это квадратное уравнение имеет два корня, положительный и отрицательный, время отрицательным быть не может, значит, нужно найти положительный корень.
По формуле это t=(корень<7*7+3*4*6>-7)/(2*6)=(11-7)/12=1/3
Подставим значение t в полученное ранее V=30t+50, получим V=10+50=60, то есть скорость автобуса — 60 км/ч.
Для решения этого уравнения достаточно 204 умножить на 59.
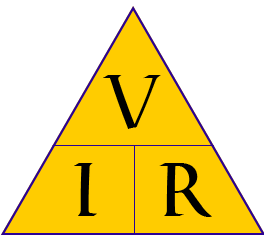
Вообще, любой подобное уравнение решается достаточно просто, методом треугольника: представьте себе в виде треугольника три цифры: одна цифра в верхнем углу треугольника и две цифры расположены по нижним углам. В верхнем углу — результат произведения умножаемого и множителя, расположенных в двух нижних углах. Закрыв рукой неизвестное — у нас на картинке сразу появится необходимое действие, для нахождения неизвестного.
На картинке отображен треугольник в виде закона Ома.
Чтобы найти V нам необходимо перемножить I и R. Чтобы найти R нам необходимо разделить V на I.
Общий ход графического решения задач. Сначала, при необходимости, как в обычных алгебраических уравнениях, можете переносить любые члены из левой части в правую или наоборот, не забыв при этом поменять знак, добиваясь, чтобы в каждой части уравнения были удобные для Вас выражения. Затем пишете функции у(л)=(левая часть уравнения) и у(п)=(правая часть уравнения). Строите графики функций у(л) и у(п). Абсциссы точек пересечения графиков (если таковые есть), дают Вам решения Вашего уравнения.
В Ваших уравнениях левая и правая части уравнений приведены к оптимальному виду.
Значит, для решения уравнения (2) Вам нужно построить графики функций y=√(x) и у=2, для решения уравнения (4) — графики функций y=√(x) и у=-х.
Берете отдельный листок в клетку. Чертите на ней оси координат с пересечением осей в центре листочка. Как можно аккуратнее и точнее чертите на нем параболу y=X^2, и обязательно прочерчиваете ось Y. Аккуратно наклеиваете листочек на картон или тонкий пластик. Аккуратно ножницами вырезаете эту параболу. Теперь у вас готов шаблон для построения графиков любых парабол.
Построение графика функции y=√(x). На странице тетради в клетку чертите оси координат. Берете изготовленный шаблон, и накладываете его горизонтально на страницу так, чтобы начала координат шаблона и в тетради совпали, о ось Y шаблона совпала с осью Х в тетради. Обводите карандашом верхнюю половину шаблона. На листочке получится половинка параболы, расположенная горизонтально. Это и есть график функции y=√(x).
Решение задачи (2). Через точку (0,5) проводите прямую, параллельную оси Х. Точка пересечения этой прямой с параболой (25,5) даст решение примера. Х=25.
Решение задачи (4). Через центр координат проводите диагональ второй и четвертой четвертей. Это будет график функции y=-x. У этой прямой и параболы имеется только одна общая точка (0;0), т.е. начало координат. Значит решением является х=0,
Источник