Реши задачу арифметически двумя способами два пешехода одновременно

4 класс. Моро. Учебник №2. Ответы к стр. 16

Фев 19

4 класс. Моро. Учебник №2. Ответы к стр. 16

Числа от 1 до 1000
Умножение на числа, оканчивающиеся нулями
Письменное умножение двух чисел, оканчивающихся нулями
Ответы к стр. 16

Учимся решать задачи: выполнять схематические чертежи, сравнивать задачи и их решения.

61. Реши задачи, сравни решения.
1 ) Два лыжника вышли одновременно навстречу друг другу из двух поселков и встретились через 3 ч. Первый лыжник шел со скоростью 12 км/ч, а второй − со скоростью 14 км/ч. Найди расстояние между поселками.

2 ) Из двух поселков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шел со скоростью 12 км/ч, а второй со скоростью 14 км/ч. Через сколько часов лыжники встретились?

3 ) Из двух поселков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шел со скоростью 12 км/ч. С какой скоростью шел второй лыжник?

1-я задача
1) 12 • 3 = 36 (км) − прошел первый лыжник
2) 14 • 3 = 42 (км) − прошел второй лыжник
3) 36 + 42 = 78 (км)
О т в е т: расстояние между поселками 78 км.

2-я задача
1) 12 + 14 = 26 (км/ч) − скорость сближения лыжников
2) 78 : 26 = 3 (ч)
О т в е т: время лыжников в пути до встречи 3 часа.

3-я задача
1) 78 : 3 = 26 (км/ч) − скорость сближения лыжников
2) 26 − 14 = 14 (км/ч)
О т в е т: скорость второго лыжника 14 км/ч.

В первом случае мы искали расстояние между поселками, умножив скорости лыжников на время в пути до встречи и сложив результаты. Во втором — время лыжников до встречи, сложив скорости лыжников и разделив расстояние между поселками на этот результат. А в третьем — скорость второго лыжника, разделив расстояние между городами на время в пути и отняв от этого результат скорость первого лыжника.

62. Составь и реши три похожие задачи про пешеходов, которые шли навстречу друг другу со скоростями 4 км/ч и 5 км/ч и встретились через 2 ч.

1-я задача.
Два пешехода вышли одновременно навстречу друг другу из двух поселков и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч, а второй − со скоростью 5 км/ч. Найди расстояние между поселками.

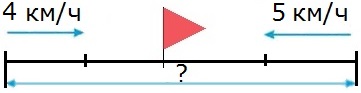
1) 4 • 2 = 8 (км) − прошел первый пешеход
2) 5 • 2 = 10 (км) − прошел второй пешеход
3) 8 + 10 = 18 (км)
О т в е т: расстояние между поселками 18 км.

2-я задача.
Из двух поселков, расстояние между которыми 18 км, вышли одновременно навстречу друг другу два пешехода. Первый из них шел со скоростью 4 км/ч, а второй со скоростью 5 км/ч. Через сколько часов пешеходы встретились?

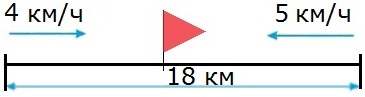
1) 4 + 5 = 9 (км/ч) − скорость сближения пешеходов
2) 18 : 9 = 2 (ч)
О т в е т: пешеходы встретились через 2 часа.

3-я задача
Из двух поселков, находящихся на расстоянии 18 км, вышли одновременно навстречу друг другу два пешехода и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч. С какой скоростью шел второй пешеход?

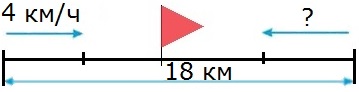
1) 18 : 2 = 9 (км/ч) − скорость сближения пешеходов
2) 9 − 4 = 5 (км/ч)
О т в е т: скорость второго пешехода 5 км/ч.

63. (Устно.) 600 : 3 + 7 • 5 40 • ( 16 − 8 ) • 2
600 : ( 3 + 7 ) • 5 40 • ( 16 − 8 • 2 )

600 : 3 + 7 • 5 = 200 + 35 = 235
600 : (3 + 7) • 5 = 600 : 10 • 5 = 60 • 5 = 300
40 • (16 − 8) • 2 = 40 • 8 • 2 = 320 • 2 = 640
40 • (16 − 8 • 2) = 40 • (16 − 16) = 40 • 0 = 0

64. 8070 • 600 5010 − 15900 : 100 + 786

5010 − 15900 : 100 + 786 = 5010 − 159 + 786 = 4851 + 786 = 5637
_ 5010 ₊4851
159 786
4851 5637

9800 • 30 30200 − 7020 : 10 • 3 + 68

30200 − 7020 : 10 • 3 + 68 = 30200 — 702 • 3 + 68 = 28094 + 68 = 28162
_×702 ₊30200
3 2106
2106 28094

ЗАДАНИЕ НА ПОЛЯХ
ЦЕПОЧКА

Источник

Реши задачу арифметически двумя способами два пешехода одновременно

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 150 метрам?

Это задание ещё не решено, приводим решение прототипа.

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?

Пусть км/ч – скорость второго пешехода, тогда скорость первого – км/ч. Пусть через часов расстояние между пешеходами станет равным 0,3 километра. Таким образом,

часа или минут.

Источник

Два пешехода одновременно вышли навстречу друг другу (см)Как решить задачу?

Два пешехода одновременно вышли навстречу друг другу из двух посёлков и встретились через 3 часа. Определить расстояние между посёлками, если один пешеход двигался со скоростью 5 км/ч, а второй — 6 км/ч.

Сначала давайте узнаем, сколько пройдут оба пешехода за один час. Для этого мы просто сложим их скорости. Вот так:

5 + 6 = 11(км) пройдут оба пешехода за 1 час.

Теперь мы также без труда можем узнать и то, сколько километров они пройдут за три часа. Найденное число и будет расстоянием между посёлками. Итак:

11 х 3 = 33(км) расстояние между посёлками.

Можем написать ответ.

Ответ: 33 км — расстояние между посёлками.

Это стандартная арифметическая задача на встречное движение. И решается она стандартно. Первый пешеход, двигаясь со скоростью 5 км/ч, прошел за 3 часа 15 км, а второй пешеход прошел 6 х 3 = 18 км. Вместе они прошли всё расстояние между двумя поселками, которое равно 15 + 18 = 33 км. Это и есть расстояние между поселками. Возможно второе решение: суммарная скорость двух пешеходов 5 + 6 = 11 км/ч, и за три часа они покроют вместе расстояние 11 х 3 = 33 км.

Известен более хитрый вариант этой задачи (часто в ней фигурируют не пешеходы, а велосипедисты). В этом варианте муха, сидящая на носу первого человека в момент его отправления путь, летит ко второму, садится ему на нос и опять летит к первому. Известна скорость мухи. И нужно найти, сколько она всего пролетела километров. Когда такую задачу задачи знаменитому математику Джону фон Нейману, от дал ответ очень быстро. А на вопрос, как он так быстро все посчитал, фон Нейман ответил: «Я просуммировал ряд, он сходится».

Скорость первого пешехода 5(км/ч), за 3 часа он пройдёт 15(км);

Скорость второго пешехода 6(км/ч), за 3 часа он пройдёт 18(км);

Поскольку они встретились, значит, общее расстояние равно 15+18=33(км);

Ответ: расстояние между посёлками 33 км;

Так как пешеходы идут навстречу друг другу, то просто сложим пройденные ими расстояния:

Расстояние = (5 км/ч * 3 ч) + (6 км/ч * 3 ч) = 15 км + 18 км = 33 км.

Ответ: расстояние составляет 33 км.

Наверняка речь идет о задание ЕГЭ номер 17 по профильной математике. Хотя задания о кредитах, вкладах, процентах по вкладу, вообще о деньгах встречаются и в базовой части. Но все они несложные и решаются в один или два приема.

Задание 17 же это уже высокого уровня сложности.

Там правда чаще встречаются задания по вкладам, но и кредиты, и вклады решаются одинаково.

Основное, что нужно знать при решении этих заданий — это формулы п-го члена и суммы геометрической прогрессии, то есть понимать, что речь идет именно о геометрической прогрессии. Иными словами нужно определить для себя, что здесь первый член прогрессии, что является знаменателем прогрессии, о каком члене прогрессии идет речь и какую сумму нужно определить.

Ясно, что знаменатель прогрессии 1,1 (10%), сумма прогрессии 2 395 800, но есть еще и дополнительные условия: три платежа и соотношения между ними. Лучше всего обозначить через х сумму первого платежа и дальше уже составлять и решать уравнения.

Источник

Реши задачу арифметически двумя способами два пешехода одновременно

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 475 метрам?

Это задание ещё не решено, приводим решение прототипа.

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?

Пусть км/ч – скорость второго пешехода, тогда скорость первого – км/ч. Пусть через часов расстояние между пешеходами станет равным 0,3 километра. Таким образом,

часа или минут.

Источник

Два пешехода одновременно вышли навстречу друг другу (см)Как решить задачу?

Два пешехода одновременно вышли навстречу друг другу из двух посёлков и встретились через 3 часа. Определить расстояние между посёлками, если один пешеход двигался со скоростью 5 км/ч, а второй — 6 км/ч.

Сначала давайте узнаем, сколько пройдут оба пешехода за один час. Для этого мы просто сложим их скорости. Вот так:

5 + 6 = 11(км) пройдут оба пешехода за 1 час.

Теперь мы также без труда можем узнать и то, сколько километров они пройдут за три часа. Найденное число и будет расстоянием между посёлками. Итак:

11 х 3 = 33(км) расстояние между посёлками.

Можем написать ответ.

Ответ: 33 км — расстояние между посёлками.

Это стандартная арифметическая задача на встречное движение. И решается она стандартно. Первый пешеход, двигаясь со скоростью 5 км/ч, прошел за 3 часа 15 км, а второй пешеход прошел 6 х 3 = 18 км. Вместе они прошли всё расстояние между двумя поселками, которое равно 15 + 18 = 33 км. Это и есть расстояние между поселками. Возможно второе решение: суммарная скорость двух пешеходов 5 + 6 = 11 км/ч, и за три часа они покроют вместе расстояние 11 х 3 = 33 км.

Известен более хитрый вариант этой задачи (часто в ней фигурируют не пешеходы, а велосипедисты). В этом варианте муха, сидящая на носу первого человека в момент его отправления путь, летит ко второму, садится ему на нос и опять летит к первому. Известна скорость мухи. И нужно найти, сколько она всего пролетела километров. Когда такую задачу задачи знаменитому математику Джону фон Нейману, от дал ответ очень быстро. А на вопрос, как он так быстро все посчитал, фон Нейман ответил: «Я просуммировал ряд, он сходится».

Скорость первого пешехода 5(км/ч), за 3 часа он пройдёт 15(км);

Скорость второго пешехода 6(км/ч), за 3 часа он пройдёт 18(км);

Поскольку они встретились, значит, общее расстояние равно 15+18=33(км);

Ответ: расстояние между посёлками 33 км;

Так как пешеходы идут навстречу друг другу, то просто сложим пройденные ими расстояния:

Расстояние = (5 км/ч * 3 ч) + (6 км/ч * 3 ч) = 15 км + 18 км = 33 км.

Ответ: расстояние составляет 33 км.

Наверняка речь идет о задание ЕГЭ номер 17 по профильной математике. Хотя задания о кредитах, вкладах, процентах по вкладу, вообще о деньгах встречаются и в базовой части. Но все они несложные и решаются в один или два приема.

Задание 17 же это уже высокого уровня сложности.

Там правда чаще встречаются задания по вкладам, но и кредиты, и вклады решаются одинаково.

Основное, что нужно знать при решении этих заданий — это формулы п-го члена и суммы геометрической прогрессии, то есть понимать, что речь идет именно о геометрической прогрессии. Иными словами нужно определить для себя, что здесь первый член прогрессии, что является знаменателем прогрессии, о каком члене прогрессии идет речь и какую сумму нужно определить.

Ясно, что знаменатель прогрессии 1,1 (10%), сумма прогрессии 2 395 800, но есть еще и дополнительные условия: три платежа и соотношения между ними. Лучше всего обозначить через х сумму первого платежа и дальше уже составлять и решать уравнения.

Источник