Реши задачу алгебраическим способом с помощью уравнения

Реши задачу алгебраическим способом с помощью уравнения

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

• Главная
• 9-Класс
• Алгебра
• Видеоурок «Алгебраический способ решения текстовых задач»

Существует несколько способов решения текстовых задач:

• арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;

• алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;

• геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;

• схематический способ – это способ решения текстовой задачи с помощью схем;

• графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.

Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели.

В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи.

В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи.

В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры.

В схематическом способе математической моделью является схема, с помощью которой находят решение задачи.

В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.

На этом занятии более подробно будет рассмотрен алгебраический способ решения задачи.

Решить текстовую задачу алгебраическим способом означает:

1. Ввести удобную переменную выразить через неё неизвестные величины.

2. По явным условиям, описанным в задаче, составить уравнение или неравенство.

3. Решить уравнение или неравенство

4. Выбрать из всех найденных решений те, которые подходят по смыслу задачи, то есть удовлетворяют неявным условиям задачи и, таким образом, найти ответ на главный вопрос задачи. Рассмотрим методику алгебраического способа решения текстовых задач с помощью уравнений и неравенств.

1 этап. Арифметическая краткая запись условий задачи.

Цель этого этапа: осмысление задачи.

Форма записи: схематический чертёж или таблица всех известных и неизвестных данных задачи.

• этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями;

• на этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно «увязать» все известные и неизвестные величины в таблицу данных задачи или составить чертёж; неизвестные величины удобно обозначать знаком «?», а «главный вопрос» задачи для того, чтобы потом на последних этапах не запутаться и правильно найти «Ответ», так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять;

• все единицы измерения перевести в единые;

• значительно облегчает решение и делает задачу более понятной введение обозначений, общепринятых в физике, химии, геометрии, алгебре, экономике и так далее. Например: V,t,s-скорость, время, расстояние (длина пути или отрезка); р,V,m-плотность вещества, объём тела, масса тела; W,t,V–производительность, время работы, объём работы; a,b,P,S–две стороны прямоугольника, его периметр, его площадь; А0,р,n,An-первоначальная величина, процент её увеличения, количество увеличений, конечная величина после увеличения А0 на р процентов n раз; MА,СА,M–масса вещества А в растворе или в смеси, концентрация вещества А в растворе или смеси (доля), масса раствора или смеси; mn=10m+n–запись двузначного числа, где m,n–цифры;

• Большую помощь в задачах «на движение» оказывает схематический чертёж. Он позволяет увидеть динамику движения, а также учесть все характерные ситуации–встречи, остановки, повороты и тому подобное.

2 этап. «Легенда» или алгебраическая краткая запись условий задачи.

Цель этого этапа: удачно выбрать переменную и выразить все неизвестные величины задачи через неё.

Форма записи: такая, как и на 1этапе, но только вместо знаков «?» везде надо записать выражения с переменной.

• обычно этот этап в оформлении задачи начинается с фразы «Пусть х ед.-…,тогда…»;

• не следует пытаться обойтись небольшим числом неизвестных; наоборот, чем больше неизвестных, тем легче составлять уравнения или неравенства;

• выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи; точнее, набор переменных представляет собой список параметров, определяющих эту модель, поэтому все они должны быть независимы, и все соотношения должны следовать лишь из конкретных условий задачи;

• при введении переменных следует руководствоваться принципом наибольшего удобства математической записи условий задачи, при этом искомая величина может не входить в их число. В большинстве задач «главный вопрос» подсказывает выбор переменной.

3 этап. Составление и решение уравнения или неравенства (системы уравнений или неравенств).

Цель этого этапа: опираясь на условия задачи составить уравнение или неравенство ( систему уравнений или неравенств ) и найти его (её) решение.

• обычно этот этап в оформлении задачи начинается словами «По условию задачи (выписать условия из текста задачи), значит,…(запись уравнения или неравенства).»;

• необходимо учитывать Область Допустимых Значений переменной или переменных помня условия существования уравнения или неравенства (системы уравнений или неравенств);

• для составления уравнения или неравенства (системы уравнений или неравенств) из текста задачи выбираем условие (условия), которое позволяет увязать известные и неизвестные данные задачи в формулы: S=vt-вычисление длины пути, пройденного телом; m=pV-вычисление массы тела; V=Wt-вычисление объёма работы;S=ab–вычисление площади прямоугольника; MА=САM-вычисление массы вещества А в смеси или растворе; An=A0(1±p)n или An=A0(1±p1) … (1±pn) вычисление сложных процентов;

• если неизвестных следует брать столько, сколько потребуется, то уравнений будет cтолько, сколько получится; в простейших ситуациях мы получаем уравнение (неравенство) с одной переменной или систему уравнений (неравенств), в которой число уравнений (неравенств) совпадает с числом неизвестных.

4 этап. Анализ решения уравнения или неравенства (системы уравнений или неравенств).

Цель: из всех найденных решений уравнений или неравенств (систем уравнений или неравенств) выбрать те, которые подходят по смыслу задачи и, по мере необходимости, довычислить искомую величину.

обычно этот этап в оформлении задачи начинается фразой «По смыслу задачи х должна быть величиной… (натуральной, положительной, целой, принадлежащей промежутку и так далее), и, если смысловое условие не выполнено, то найденную величину называют посторонним решением, а , если смысловое условие выполнено, то записывают единицы измерения и пояснение к найденной величине.

• т.о., не каждое решение уравнения может являться решением задачи; особенности отбора значений переменных в различных типовых задачах будут рассмотрены ниже;

• для всякой текстовой задачи полезно провести проверку её решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.

Цель этого этапа: записать правильный ответ, удовлетворяющий всем описанным условиям задачи и отвечающий на её «главный вопрос».

Рассмотрим полное решение задачи по указанной схеме.

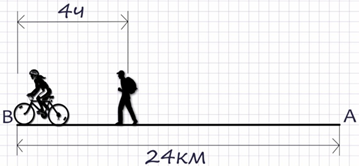
Задача. Из пункта А в пункт В, расположенный в 24км от А, одновременно отправились пешеход и велосипедист. Велосипедист прибыл в пункт В на 4часа раньше пешехода. Известно, что если бы велосипедист ехал с меньшей на 4км/ч скоростью, то на путь из А в В он затратил бы вдвое меньше времени, чем пешеход. Найти скорость пешехода.

1 этап. Арифметическая краткая запись.

По условию задачи надо определить скорость пешехода, значит, это и является «Главным вопросом» задачи.

2 этап. «Легенда» или алгебраическая краткая запись. Поскольку путь от А до В известен, то неизвестные величины–скорости пешехода и велосипедиста и время их движения. Т.к. «главный вопрос» задачи–скорость пешехода, то обозначим за переменные скорости, а время выразим через введенные неизвестные. Пусть х км/ч–скорость пешехода, у км/ч–скорость велосипедиста, тогда

В задаче описаны два условия движения пешехода и велосипедиста, значит, получим два уравнения «увязанные» с изменением времени движения.

3 этап. Составление и решение системы уравнений.

24(х + 2) – 12х – 4х(х + 2) = 0, х(х + 2)≠ 0 – ОДЗ. х2-х-12=0; По теореме Виета х1 х2=-12, х1+х2=1. Получаем два решения первого уравнения системы: х1=4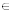ДЗ,

х2=-3ОДЗ. Оба решения удовлетворяют неравенству системы, т.е. ОДЗ дробно–рационального уравнения.

4 этап. Анализ решения системы уравнений.

По смыслу задачи х–положительное число, х=-3 постороннее решение,

х=4>0 =>4км/ч скорость движения пешехода.

Проверка решения задачи.

Она часто бывает полезна, но не обязательна. В задаче поставлены четыре условия существования искомой величины–скорости пешехода: 1условие–расстояние между пунктами А и В 24км; 2условие–время движения велосипедиста меньше времени движения пешехода на 4часа; 3условие–изменённая скорость велосипедиста на 4км/ч меньше фактической скорости; 4условие–изменённое время движения велосипедиста в 2раза меньше времени движения пешехода. Для проверки достоверности решения допустим выполнение двух из них при найденном решении задачи. Если два других условия при этом выполнятся, то будем считать, что задача решена верно. Если два других условия не выполнятся, то решение найдено неверно.

24км:4км/ч = 6ч – время движения пешехода; (использовали 1 условие)

6ч – 4ч = 2ч – время движения велосипедиста; (использовали 2 условие)

24км:2ч = 12км/ч – скорость движения велосипедиста;

12км/ч – 4км/ч = 8км/ч – изменённая скорость велосипедиста;

24км:8км/ч = 3ч – изменённое время движения велосипедиста; (выполнено 3 условие)

6ч:3ч = 2(раза) – отношение времени движения пешехода и велосипедиста; (выполнено 4 условие)

Все условия задачи выполнены =>скорость пешехода 4км/ч найдена верно.

5 этап. Ответ. Ответ: 4км/ч.

Таким образом, на этом занятии мы познакомились с алгебраическим способом решения текстовой задачи и разобрали методику её решения на примере задачи «на движение».

Источник

Решение задач алгебраическим методом
методическая разработка по алгебре (5 класс)

Знакомство с алгебраическим методом решения текстовых задач

Скачать:

Вложение	Размер
reshenie_tekstovyh_zadach_algebraicheskim_metodo1.docx	26.38 КБ
reshenie_tekstovyh_zadach_algebraicheskim_metodo1.docx	26.38 КБ

Предварительный просмотр:

РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ

Лиханова В.Е., учитель математики МБОУ «СОШ №12» г. Ноябрьск, ЯНАО

Наряду с арифметическим, практическим методами решения задач ученики 5 класса знакомятся и с алгебраическим методом. Многие ученики сначала не будут принимать новый метод, поэтому роль учителя на данном этапе должна заключаться в том, чтобы показать преимущества данного метода, но ни в коем случае не навязывать его. С этой целью необходимо предлагать задачи, которые арифметически решить трудно.

Особенностями алгебраического метода является введение переменной величины, что позволяет действовать с ней как с явной. Выполняется анализ основных зависимостей между явными и неявными значениями величин, производится моделирование условия задачи в виде уравнения. Если при выборе действий опираемся на сюжетные особенности, то такой метод решения называется алгебраическим. Следует отметить, что в учебнике «Математика 5» авторского коллектива: Г.В.Дорофеев, И.Ф. Шарыгин, Е.А. Бунимович, Л.В. Кузнецова существуют определенные недостатки по обучению решению задач алгебраическим методом. Самым главным из них является недостаточность системы упражнений, готовящих детей к усвоению данного метода, а именно на составление различных выражений по сюжету задач и выяснение их сюжетного смысла.

Необходимые базовые знания для решения задач алгебраическим методом:

• усвоение понятия переменной величины;
• умение решать простые и составные уравнения;
• умение составлять по тексту задачи простые и составные выражения и определять их сюжетный смысл;
• находить выражения с одинаковым сюжетным смыслом.

Основные этапы формирования умения решать задачи алгебраическим методом:

1. Подготовительный.
2. Этап ознакомления с алгоритмом рассуждения и записью решения задачи.
3. Закрепление, выработка умения.

На первом этапе учитель должен познакомить учащихся с понятием «сюжетный смысл выражения», научить составлять всевозможные выражения по тексту задачи, определять их сюжетный смысл. Это можно сделать через следующую систему упражнений:

1. Дать текст с числами. Составить по этому тексту несколько выражений, записать их смысл.
2. Дать текст. Учитель составляет по этому тексту выражения, а ученики объясняют их смысл по тексту.
3. Предложить задание, подобное предыдущему, но среди выражений должны быть такие, которые не имеют сюжетного смысла по данному тексту.
4. По предложенному тексту с числами дети сами составляют выражения и определяют их смысл. В заключение находят выражения с одинаковым сюжетным смыслом.
5. Дать задачу, показать способ обозначения величины, которую требуется найти в вопросе задачи через х, показать способ составления выражений по задаче с использованием этой неизвестной величины как с известной. Определить сюжетный смысл выражений по тексту задачи.
6. По предложенному тексту учитель показывает сюжетный смысл одного из выражений. Детям предлагается составить выражение с тем же сюжетным смыслом.

У пруда росли липы, осины, березы и ели. Лип росло 12, осин – в 3 раза больше, чем лип, несколько елей, берез – на 5 меньше, чем елей. Составь различные выражения и объясни, что они обозначают.

Учитель предлагает обозначить число елей буквой х , работать с ней как с обыкновенным числом. Можно составить следующие выражения:

12·3 – количество осин,

х-5 – количество берез,

12+х – количество лип и елей,

12+(х-5) – количество лип и берез,

12·3+(х-5)+х –общее количество осин, берез, елей.

Основная задача второго этапа – введение понятия «основание для составления уравнения», введение алгоритма рассуждения и развернутой формы записи решения задачи алгебраическим методом. Деятельность учителя может быть организована следующим образом.

1. Дать текст задачи. Решить ее арифметическим методом.
2. Предложить обозначить через х неизвестную величину, значение которой требуется найти.
3. Составить ряд выражений по тексту и определить их сюжетный смысл.
4. Найти выражения с одинаковым сюжетным смыслом. Сообщить детям, что если выражения имеют одинаковый смысл, то они равны.
5. Составить равенство из двух выражений, в одно из которых входит переменная.
6. Вместе с детьми определить, что данная запись является уравнением.
7. Решить его и установить, что значение х и есть ответ.
8. Сообщить учащимся, что сюжетный смысл выражений, которые мы использовали для составления уравнения, будем называть основанием для составления уравнения, а метод решения задачи – алгебраическим.
9. Решить еще одну задачу таким же методом. Запомнить алгоритм рассуждений и полную форму записи решения задачи.
10. Решив другую задачу, учитель предлагает проверить правильность решения задачи. Для этого необходимо вспомнить все известные способы проверки правильности решения, которые использовали ранее.
11. Сообщить детям новый способ проверки. Для этого надо составить уравнение по другому основанию. Сделать вывод.
12. Сопоставляя решения первой и второй задачи, учитель в процессе фронтальной беседы составляет алгоритм решения задачи алгебраическим методом.

Алгоритм решения задачи алгебраическим методом.

1. Обозначить буквой неизвестную величину.
2. Составить выражения.
3. Выбрать основание.
4. Составить уравнение.
5. Решить уравнение.

6. Проверить правильность решения.

Знакомство с новым методом решения задачи можно начать:

• с простой задачи;
• сразу с составной.

В первом случае работа будет выполняться достаточно быстро, но учащиеся не увидят преимущества данного метода (ведь задача и так решена !).

Рассмотрим задачу. Ученики изготовили 135 елочных украшений, из них фонариков на 5 больше, чем хлопушек, а снежинок в 3 раза больше, чем снежинок. Сколько хлопушек изготовили дети?

Необходимо показать, что задача решается с помощью уравнения. Для этого надо ввести переменную величину. Обозначить буквой можно как число хлопушек, так и число фонариков, так и число снежинок (проще — число хлопушек). Составляем выражения с переменной.

Хлопушки- ? штук

Фонарики-?, на 5 штук больше 135 штук

Снежинки-?, в 3 раза больше

Пусть х штук хлопушек сделали дети, тогда они изготовили (х+5) штук фонариков, 3х штук снежинок. Всего было сделано (х+(х+5)+3х) штук украшений , а это – 135 штук украшений. Выражения ( х+(х+5)+3х ) и 135 имеют один и тот же сюжетный смысл, значит, их можно приравнять. Требуется подчеркнуть, чту уравнивать можно только выражения, имеющие одинаковый сюжетный смысл. Получится уравнение:

х+(х+5)+3х=135. Обратить внимание, что в уравнении наименования не пишутся. Решим уравнение

Итак, 26 хлопушек сделали дети.

Предложить решить задачу арифметическим методом . Без вспомогательной модели это сделать трудно. Составим схематический чертеж.

Хл.

Ф. 5 ш. 135 ш.

Сн. .

Все украшения можно разделить на 5 равных частей, если бы не было5 штук фонариков. Уберем их, при этом общее количество уменьшится на 5.

1) 135-5=130 (шт.) — украшений всего.

1. 130:5=26 (шт.) – в одной части , т.е. столько хлопушек сделали дети.

В задачах с пропорциональными величинами желательно использовать таблицу не только для краткой записи содержания, но и для проведения рассуждений при составлении уравнения. Сначала в таблице записывается содержание задачи, а затем (желательно другим цветом) заполняются все пустые графы выражениями с переменной величиной.

Из двух городов, расстояние между которыми 1620 км вышли одновременно навстречу друг другу два поезда, скорость одного на 10 км/ч больше скорости другого и через 18 часов они встретились. Какова скорость каждого поезда?

Скорость

Расстояние

(х+10)км/ч На 10 км/ч больше

Источник