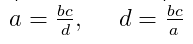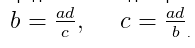6.1.2. Задачи на пропорцию
Задача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?
Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:
3,3:300 или х:500.
Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений):
3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: «6.1.1. Пропорция. Основное свойство пропорции.»)
х=(3,3·500):300;
х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см.
Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:
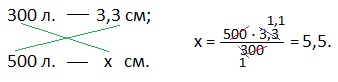
или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.
Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе.
Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?
Решение.
Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.
5:100 или х:98. Получаем пропорцию:
5:100 = х:98.
х=(5·98):100;
х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды.
Задача 3. Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?
Решение.
Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:
16,8:21 или х:35. Получаем пропорцию:
16,8:21=х:35.
Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (21). Сократим дробь на 7.
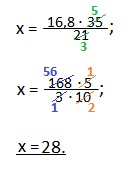
Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3).
Ответ: 35 литров нефти имеют массу 28 кг.
Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?
Решение.
Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:
х:100 или 9:18. Составляем пропорцию:
х:100 = 9:18.
Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член (18). Сокращаем дробь.
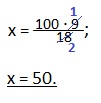
Ответ: площадь всего поля 50 га.
Источник
Задачи на пропорции
О чем эта статья:
5 класс, 7 класс, 8 класс
Понятие пропорции
Чтобы решать задачи на тему пропорции, вспомним главное определение.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.
Главное свойство пропорции:
Произведение крайних членов равно произведению средних.
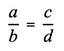
где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.
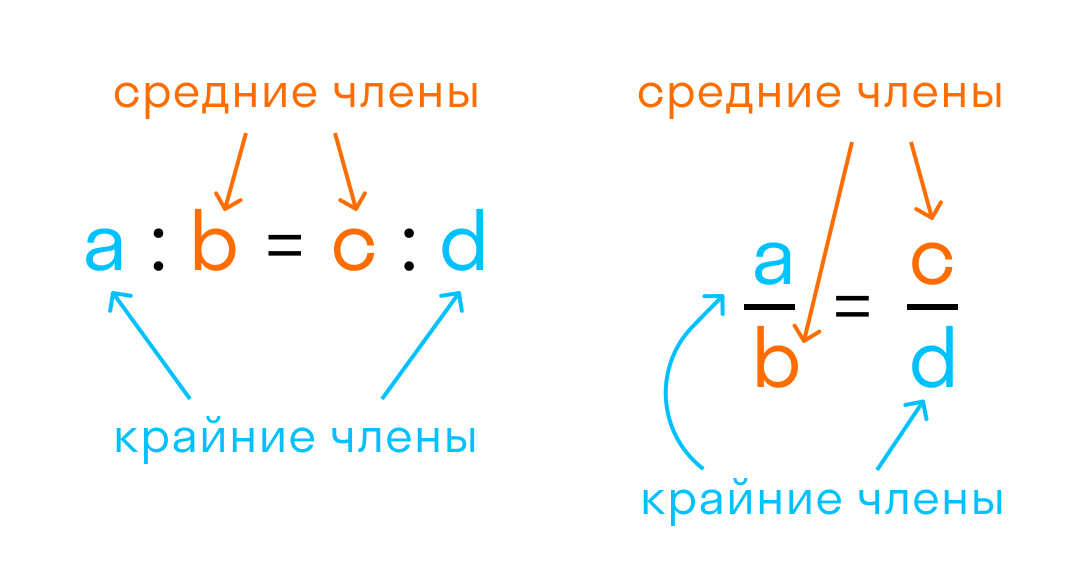
Вывод из главного свойства пропорции:
- Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
- Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:
Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.
Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.
Задачи на пропорции с решением и ответами
Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.
Задание 1. Найти неизвестный член пропорции: x/2 = 3/1
В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:
Задание 2. Найти неизвестный член: 1/3 = 5/y
Задача 3. Решить пропорцию: 30/x = 5/8
Задание 4. Решить: 7/5 = y/10
Задание 5. Известно, что 21x = 14y. Найти отношение x — к y
- Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.
На следующем примере мы узнаем как составить пропорцию по задаче💡
Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?
- Примем всех подписчиков за 100% и запишем условие задачи кратко:
Ответ: 36% всех подписчиков поставили лайк под постом.
Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?
- Составим пропорцию: 5/2 = x/450.
- Найдем х: (5 * 450) : 2 = 1125.
Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.
Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?
Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.
Ответ: в 5 кг арбуза содержится 4,9 кг воды.
Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.
Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
- Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.
Подставим известные значения: 75/52 = t2/13
t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин
Ответ: 18 часов 45 минут.
Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:
- Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:
Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:
Источник
Решение задач с помощью пропорций
Часто на практике приходится решать задачи, которые наиболее целесообразно делать с помощью пропорций. Если в условиях имеются две связанные величины, то для решения такую задачу удобно приводить к равенству дробей. Дробь еще называют отношением. Например, дробь 
, или 2:3 – это отношение двух к трем. Если два отношения равны друг другу, говорят о пропорции. Например, 
. Если вычислить значения выражений слева и справа от знака «=», можно убедиться, что они равны между собой. Это означает, что они являются пропорцией.
Равенство словесно выражается так: «Десять относится к пяти, как 30 относится к пятнадцати», или «Десять больше пяти во столько же раз, во сколько тридцать больше пятнадцати». Очевидно, что в пропорции фигурируют 4 числовых значения – 4 члена. Если любой из них неизвестен, его можно вычислить по трем другим членам.
Пример 1
Чтобы вычислить x, достаточно умножить обе части на 20:
Подставим найденное значение вместо x и проверим правильность решения:
Правую часть можно сократить на 4:
Таким образом, при найденном значении x=12 равенство верно.
Пример 2
Умножим обе части на 
:
, или
Для проверки подставим найденное значение вместо x:
Правая часть сокращается на 2:
= 7/6
Итак, при вычисленном значении x=6 равенство верно.
Основное свойство пропорции
Если a:b=c:d, то a и d являются крайними членами этой пропорции, b и c – средними. Основное свойство заключается в следующем: произведение крайних членов равно произведению средних: ad=bc. При записи в виде равенства дробей 
крайние и средние члены образуют 2 диагонали в форме креста. И основное свойство можно ради наглядности формулировать по-другому: произведения членов, составляющих правую диагональ, равно произведению членов, образующих левую диагональ («правило креста»). Чтобы убедиться, что данное свойство действительно присуще пропорции 
, достаточно умножить обе ее части на bd:
Сократив обе части, избавимся от знаменателей и получим:
Используя основное свойство, можно легко и быстро находить неизвестный член.
Пример 3
По основному свойству:
X=
=40
Проверим правильность решения:
Правую часть сократим на 5:
Таким образом, при полученном значении x=40 равенство верно.
Прямая и обратная зависимость
Допустим, имеются два изменяющихся параметра x и y. Причем, увеличение или уменьшение любого из них в некоторое число раз влечет за собой подобное изменение и другого в такое же число раз. В этом случае говорят о прямой зависимости, или прямой пропорциональности величин между собой: x прямо пропорционален величине y, y прямо пропорционален параметру x. Прямо пропорциональными являются такие пары как объем вещества и его масса, скорость движения и пройденное расстояние за некоторое время, количество работников и объем работы, который они способны выполнить за определенное время и т. д.
Задача 1
Человек проходит расстояние от своего дома до троллейбусной остановки (250 м) за 5 минут, до автобусной – за 7 минут. Какое расстояние от дома до остановки автобуса?
Так как увеличилось время, затраченное на дорогу, очевидно, что увеличилось и пройденное расстояние. Причем, оба этих параметра возросли в одинаковое количество раз: отношение первого расстояния ко второму равно отношению первого промежутка времени ко второму. Таким образом, расстояние и время на его прохождение прямо пропорциональны между собой. Выразим задачу равенством дробей и решим ее с помощью основного свойства:
x=
=350 м
Ответ: расстояние до автобусной остановки составляет 350 м
Предположим, имеются два переменных параметра x и y. Причем, увеличение любого из них в некоторое число раз приводит к уменьшению другого в то же число раз. И наоборот, уменьшение любого из них в какое-либо количество раз приводит к увеличению другого в это же количество раз. Другими словами, увеличение какого-либо параметра соответствует увеличению другого в обратное число раз. В этом случае говорят об обратной зависимости: x обратно пропорционален y, y обратно пропорционален x.
Задача 2
Плывя со скоростью 45 км/ч, катер прошел некоторый путь за 4 ч. За какое время он пройдет этот же путь при скорости 40 км/ч?
Так как скорость катера уменьшилась, времени на проплывание ему потребуется больше. Значит, скорость и время обратно пропорциональны друг другу. Таким образом, отношение первой скорости ко второй равно отношению второго промежутка времени к первому:
X = 
Ответ: при скорости 40 км/ч катер пройдет данный путь за 
часа.
Задача 3
Вася выполнил требуемое количество отжиманий за 1 минуту. Ваня отжимается в 
раза быстрее. За какое время Ваня отожмется требуемое количество раз?
Поскольку Ваня отжимается быстрее Васи, то времени ему потребуется меньше. Причем, ванин промежуток времени будет во столько же раз меньше, во сколько раз больше его быстрота (в раза). Таким образом, время выполнения одинакового количества отжиманий и быстрота обратно пропорциональны между собой. Обозначим время отжиманий Вани как x, тогда
x = 1 мин : = 
= 
мин
Несмотря на наличие в условиях обратной зависимости, в данном случае для решения нет смысла использовать равенство дробей.
Источник
